Приложение а

Вычислите определитель с помощью элементарных преобразований

(1)= (2)= (3)

= (4) =-10 (5) = -10 (6) = -10 (7)= -10 (-7) (8) = 70

(1)-(8) Указан порядок действий

1 Поменяем местами первую и вторую строки

2 Помножим элементы первой строки на (-3) и сложим с соответствующими элементами второй строки, помножим элементы первой строки на (2) и сложим с соответствующими элементами третий строки, помножим элементы первой строки на (-1) и сложим с соответствующими элементами четвертой строки

3 Разложим полученный определитель по элементам первого столбца

4 Выносим общий множитель элементов 3-ого столбца (10) и 1-й строки (-1)за знак определителя

5 Помножим элементы первой строки на (-1) и сложим с соответствующими элементами второй строки, помножим элементы первой строки на (-1) и сложим с соответствующими элементами третий строки

6 Разложим полученный определитель по элементам первого столбца

7 Вычислим определитель второго порядка

8 Найдем значение данного определителя

Приложение б

Алгоритм решения матричного уравнения

где , ,

Структура алгоритма

Определитель матрицы

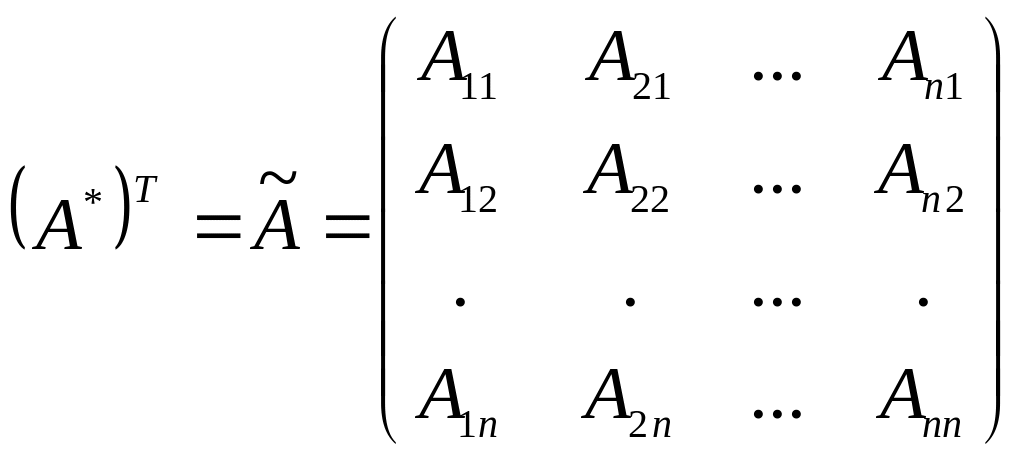
Обозначения:

- определитель матрицы

- обратная матрица

- алгебраическое дополнение элемента

- минор элемента

- матрица составленная из алгебраических дополнений

- транспонированная матрица

- союзная матрица

- не существует