П.3 Замена переменной в определенном интеграле

Теорема Пусть непрерывна на отрезке , имеет непрерывную производную на интервале , отображает отрезок на отрезок так, что , . Тогда справедлива формула замены переменной в определенном интеграле:

.

Доказательство. Пусть – первообразная для , тогда – первообразная для функции .

По формуле Ньютона-Лейбница, имеем: .

С другой стороны,

Так как правые части равенств равны, то и левые равны ■

Пример Вычислить интеграл .

Решение.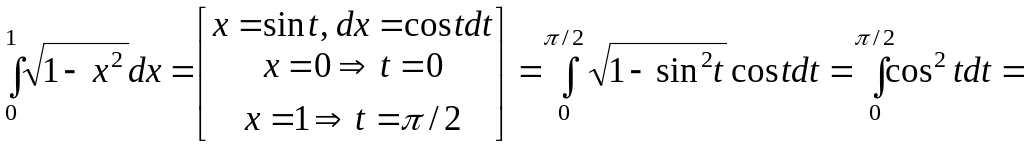

.

Утверждение 1 а) если – нечетная функция, то R;

б) если – четная функция, то R.

Доказательство. а) Так как – нечетная, то . Сделаем замену в интеграле:

.

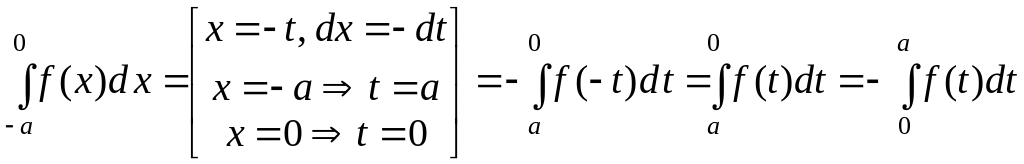Тогда .

б) Так как – четная, то . Сделав такую же замену, получим

.

Тогда ■

Утверждение 2 Если – периодическая функция с периодом Т, то R имеет место равенство:

.

Доказательство. По свойствам интеграла,

В последнем интеграле сделаем замену: . Если , то . Тогда

.

Значит, ■

П.4 Интегрирование по частям в определенном интеграле

Теорема Если функции и имеют на отрезке непрерывные производные, то справедлива формула интегрирования по частям:

.

Для доказательства достаточно проинтегрировать на отрезке равенство и учесть, что .

§ 6 Приложения определенного интеграла п.1 Вычисление площади плоской фигуры

О. Криволинейной трапецией называется фигура , задаваемая на плоскости условиями: , где – непрерывная на функция.

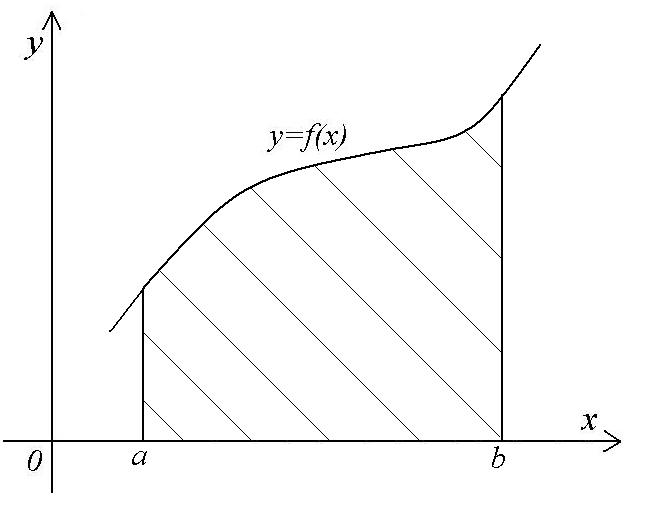
Утверждение Площадь криволинейной трапеции вычисляется по формуле:

.

Доказательство. Пусть разбиение отрезка ,

, , , , .

Рассмотрим фигуру , составленную из прямоугольников , у которых длина основания равна , а высота . А также рассмотрим фигуру , составленную из прямоугольников , длина основания которых равна , а высота , .

Очевидно, . Площади фигур и соответственно равны:

, ,

где и – нижняя и верхняя суммы Дарбу функции .

Значит, .

Так как непрерывна на , то она интегрируема на . По критерию интегрируемости , при , т.е.

. Значит, и ■

Рассмотрим фигуру , ограниченную отрезками прямых и графиками непрерывных функций и , где при . Если , то площадь фигуры равна разности площадей криволинейных трапеций, поэтому

.

Последняя формула остается верна и в случае, когда условие не выполняется.

Пример Найти площадь фигуры, ограниченной эллипсом .

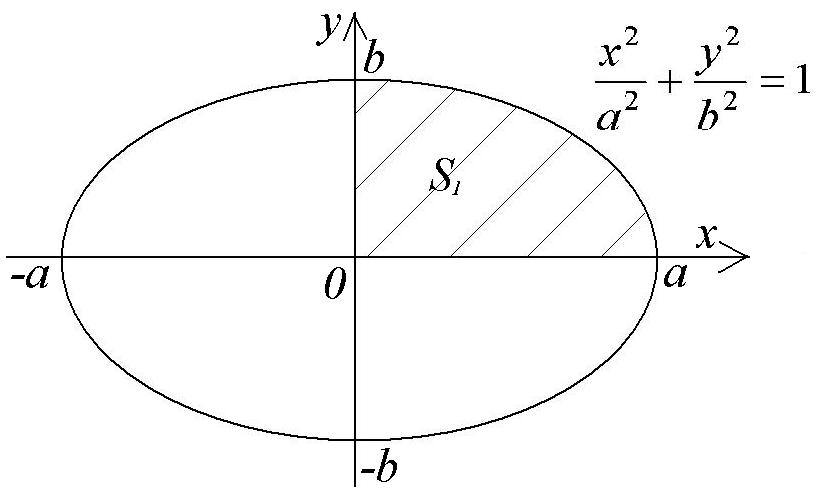
Решение. Найдем площадь части эллипса, расположенной в первой координатной четверти. Из уравнения эллипса , . Тогда искомая площадь

.

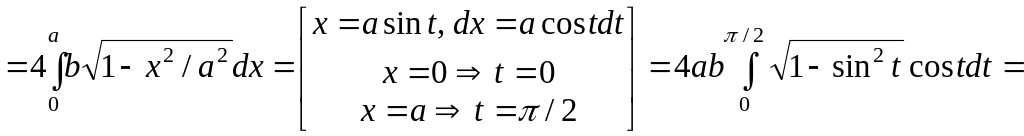
Аналогично (при ) можно вычислить площадь круга .

П.2 Площадь криволинейного сектора

Пусть кривая Г задана в полярной системе координат уравнением , . Тогда плоскую фигуру , ограниченную кривой Г и отрезками лучей называют криволинейным сектором.

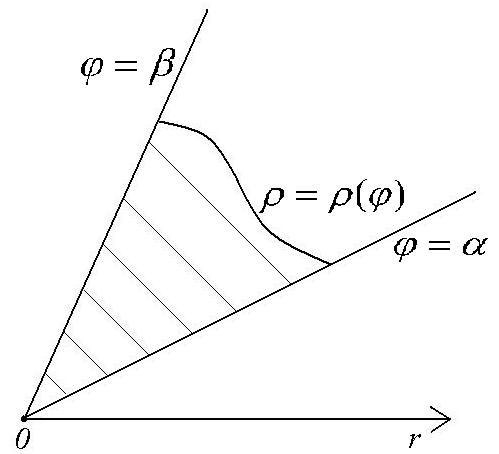
Утверждение Площадь криволинейного сектора вычисляется по формуле:

.

Доказательство. Пусть разбиение отрезка ,

, , , , .

Обозначим и – круговые секторы, ограниченные лучами , и дугами окружностей радиусов и соответственно. Тогда .

Величины и совпадают соответственно с нижней и верхней суммами Дарбу функции . Поэтому при получим

■