П.4 Достаточное условие интегрируемости функции

Пусть функция определена на отрезке и ограничена на нем. Возьмем какое-нибудь разбиение Т отрезка точками . Обозначим

, ,

, .

Числа и называются соответственно верхней и нижней суммами Дарбу функции при заданном разбиении Т отрезка .

Очевидно, при любом выборе отмеченных точек .

Критерий интегрируемости функции Для того, чтобы функция , определенная на отрезке , была интегрируемой на этом отрезке, необходимо и достаточно, чтобы эта функция была ограничена на этом отрезке и удовлетворяла условию:

,

т.е. при .

Существует другая формулировка критерия интегрируемости.

Теорема Ограниченная функция интегрируема на отрезке тогда, и только тогда, когда существуют и равны пределы:

и .

При этом общее значение этих пределов равно значению интеграла Римана, т.е. .

П.5 Классы интегрируемых функций

Теорема 1 Если функция непрерывна на отрезке, то она интегрируема на этом отрезке.

Доказательство. Так как непрерывна на отрезке, то (по теореме Кантора) она равномерно непрерывна на нем, т.е.

.

Возьмем произвольное разбиение с мелкостью . Тогда

.

Значит, интегрируема на отрезке ■

Теорема 2 Если функция ограничена на отрезке и имеет на нем лишь конечное число точек разрыва, то интегрируема на отрезке .

Теорема 3 Если функция определена на отрезке и монотонна на нем, то она интегрируема на этом отрезке.

Доказательство. Пусть, например, функция возрастает на отрезке , тогда . Но отсюда следует, что ограничена на .

Рассмотрим произвольное разбиение Т отрезка .

Так как возрастает, то для

, .

Тогда

.

Получили, что при . А это значит, что интегрируема на отрезке ■

§ 4 Свойства определенного интеграла п.1 Другая формулировка критерия интегрируемости

В параграфе 3 был сформулирован критерий интегрируемости функции:

интегрируема на отрезке ограничена на и выполняется условие: при .

Обозначим . Величину называют колебанием функции на отрезке . Тогда критерий интегрируемости запишется в виде:

интегрируема на отрезке ограничена на и выполняется условие: при .

Очевидно, .

Далее будем рассматривать только ограниченные функции.

П.2 Свойства, связанные с операциями над функциями

Свойство 1 Если функции и интегрируемы на отрезке , то R функция интегрируема на отрезке и выполняется равенство:

.

Доказательство. Составим интегральные суммы для функций , , при заданном разбиении отрезка и зафиксируем отмеченные точки . Тогда имеет место равенство:

.

Перейдем к пределу при . Так как функции и интегрируемы на отрезке , то правая часть имеет предел, равный . Тогда и левая часть имеет такой же предел ■

Свойство 2 Если функции и интегрируемы на отрезке , то функция тоже интегрируема на отрезке .

Доказательство. Если и интегрируемы на отрезке , то они ограничены на нем, т.е. R : и . Значит, ограничена на .

Рассмотрим . Тогда

.

Тогда .

Умножим последнее равенство на и просуммируем по , получим .

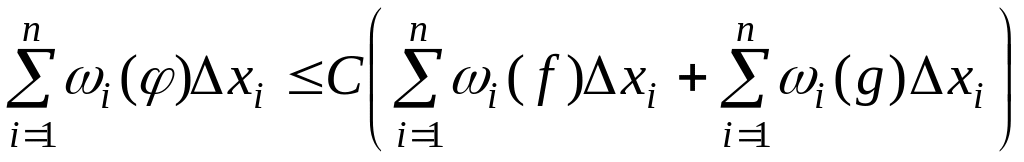При правая часть стремится к нулю, значит, и левая стремится к нулю. Значит, интегрируема на отрезке ■