
- •§ 3 Определенный интеграл п.1 Задачи, приводящие к понятию определенного интеграла
- •П.2 Определение интеграла Римана
- •П.3 Необходимое условие интегрируемости функции
- •П.4 Достаточное условие интегрируемости функции
- •П.5 Классы интегрируемых функций
- •§ 4 Свойства определенного интеграла п.1 Другая формулировка критерия интегрируемости
- •П.2 Свойства, связанные с операциями над функциями
- •П.3 Свойства, связанные с отрезками интегрирования
- •П.4 Оценки интегралов
- •П.5 Интегральная теорема о среднем
- •§ 5 Интеграл с переменным верхним пределом
- •П.1 Определение и свойства интеграла с переменным верхним пределом
- •П.3 Замена переменной в определенном интеграле
- •П.4 Интегрирование по частям в определенном интеграле
- •§ 6 Приложения определенного интеграла п.1 Вычисление площади плоской фигуры
- •П.2 Площадь криволинейного сектора
- •П.3 Вычисление объемов тел
- •П.4 Вычисление длины дуги кривой
- •П.5 Вычисление площади поверхности вращения
- •§ 7 Несобственные интегралы п.1 Определения несобственных интегралов
- •П.2 Свойства несобственных интегралов
- •П.3 Признаки сходимости несобственных интегралов
- •П.4 Абсолютно и условно сходящиеся интегралы
- •П.5 Признаки Дирихле и Абеля сходимости интегралов
§ 3 Определенный интеграл п.1 Задачи, приводящие к понятию определенного интеграла
а) Площадь криволинейной трапеции.
Пусть функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() и
и
![]() .
Рассмотрим фигуру, ограниченную отрезками
прямых
.
Рассмотрим фигуру, ограниченную отрезками
прямых
![]() и графиком функции
и графиком функции
![]() .
Такую фигуру называют криволинейной
трапецией.
.
Такую фигуру называют криволинейной
трапецией.
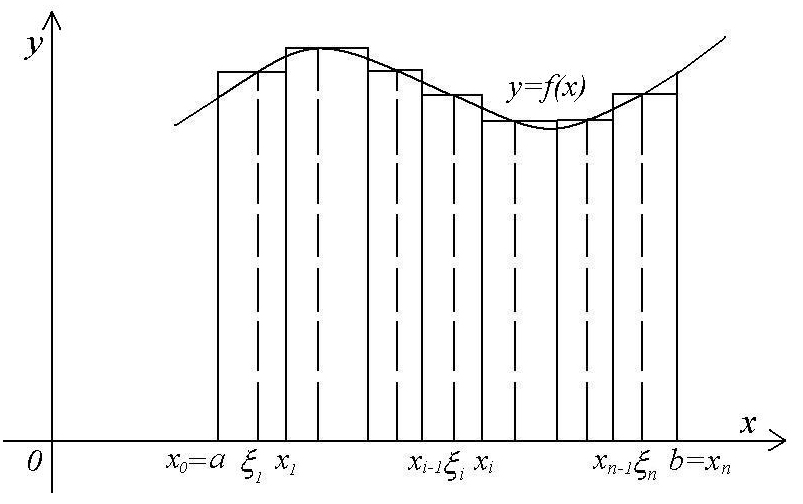
Разобьем отрезок
на n
частей
точками
![]() ,
,
![]() ,
где
,
где
![]() .
Проведем через эти точки прямые,
параллельные оси
.
Проведем через эти точки прямые,
параллельные оси
![]() .
Криволинейная трапеция разобьется на
n
криволинейных
трапеций. Обозначим
.
Криволинейная трапеция разобьется на
n
криволинейных
трапеций. Обозначим
![]() .
Пусть
.
Пусть
![]() ,
где
,
где
![]() .
Тогда сумма
.
Тогда сумма
![]() равна площади ступенчатой фигуры,
состоящей из прямоугольников шириной
равна площади ступенчатой фигуры,
состоящей из прямоугольников шириной
![]() и высотой
и высотой
![]() .
Ясно, что при достаточно мелком разбиении
площадь криволинейной трапеции будет
мало отличаться от площади полученной
ступенчатой фигуры.
.
Ясно, что при достаточно мелком разбиении
площадь криволинейной трапеции будет
мало отличаться от площади полученной
ступенчатой фигуры.
б) Движение с переменной скоростью.
Допустим,
точка движется вдоль прямой со скоростью
![]() .
Надо найти положение точки в момент
времени t,
т.е. функцию
.
Надо найти положение точки в момент
времени t,
т.е. функцию
![]() .
.
Зная
промежуток времени
![]() ,
разобьем его точками
,
разобьем его точками
![]() .
Пусть
.
Пусть
![]() .
При достаточно мелком разбиении
.
При достаточно мелком разбиении
![]() ,
где
,
где
![]() .
.
Тогда
![]() .
.
Чем
меньше
![]() ,
тем точнее
получится
пройденный путь
,
тем точнее
получится
пройденный путь
![]() .
.
Т.е.
![]() ,
где
,
где
![]() .
.
П.2 Определение интеграла Римана
Пусть
функция
определена на отрезке
.
Разбиением
Т
отрезка
называется множество точек
![]() ,
таких, что
,
таких, что
![]() .
Обозначим
– частичный
отрезок разбиения,
– длину
.
Обозначим
– частичный
отрезок разбиения,
– длину
![]() того
отрезка разбиения.
того
отрезка разбиения.
![]() назовем мелкостью
разбиения Т.
Возьмем на каждом отрезке разбиения
произвольную точку
назовем мелкостью
разбиения Т.
Возьмем на каждом отрезке разбиения
произвольную точку
![]() .
Получим разбиение с отмеченными точками.
.
Получим разбиение с отмеченными точками.
Сумма
![]() называется
интегральной
суммой
для функции
при заданном разбиении Т
и
фиксированных отмеченных точках
называется
интегральной
суммой
для функции
при заданном разбиении Т
и
фиксированных отмеченных точках
![]() .
.
О.
Число
I
называется
определенным
интегралом от функции
по
отрезку
,
если для
![]() такое, что для любого разбиения Т,
мелкость которого
такое, что для любого разбиения Т,
мелкость которого
![]() меньше
меньше
![]() ,
и при любом выборе отмеченных точек
,
и при любом выборе отмеченных точек
![]() выполняется неравенство:
выполняется неравенство:
![]() .
.
Обозначается
определенный интеграл
![]() .
.
Данное
определение интеграла означает, что
число I
является пределом интегральных сумм
![]() при
мелкости разбиения
,
стремящейся к нулю, т.е.
при
мелкости разбиения
,
стремящейся к нулю, т.е.
![]() ,
причем предел этот не зависит от выбора
отмеченных точек
.
,
причем предел этот не зависит от выбора
отмеченных точек
.
Если для функции существует число I, то функцию называют интегрируемой (по Риману) на отрезке , и говорят, что существует интеграл от функции на отрезке .
П.3 Необходимое условие интегрируемости функции
Теорема Если функция интегрируема на отрезке , то она ограничена на этом отрезке.
Доказательство.
Пусть функция
интегрируема на отрезке
.
Тогда существует число I,
удовлетворяющее определению интеграла.
В частности, для
![]()
![]()
![]() ,
т.е.
,
т.е.
![]() .
.
Зафиксируем
разбиение Т
с
мелкостью
![]() .
Допустим, что
не ограничена на отрезке
.
Тогда она не ограничена по крайней мере
на одном из отрезков
.
Допустим, что
не ограничена на отрезке
.
Тогда она не ограничена по крайней мере
на одном из отрезков
![]() разбиения Т.
Будем для определенности считать, что
не ограничена на отрезке
разбиения Т.
Будем для определенности считать, что
не ограничена на отрезке
![]() .
.
Зафиксируем
точки
![]() и обозначим
и обозначим
![]() .
.
Получим
![]() .
.
Отсюда
![]() .
.
Но
это значит, что
ограничена на
![]() .
Мы пришли к противоречию с предположением.
Значит,
ограничена на
■
.
Мы пришли к противоречию с предположением.
Значит,
ограничена на
■
Замечание.
Из ограниченности функции не следует
её интегрируемость. Например, функция
Дирихле
![]() ограничена, но не интегрируема на отрезке
ограничена, но не интегрируема на отрезке
![]() .
Действительно, если взять
.
Действительно, если взять
![]() Q,
то
Q,
то
![]() .
Если
взять из R\Q,
то
.
Если
взять из R\Q,
то
![]() .
Т.к. предел интегральных сумм не должен
зависеть от выбора отмеченных точек
,
то в данном случае его не существует.
.
Т.к. предел интегральных сумм не должен
зависеть от выбора отмеченных точек
,
то в данном случае его не существует.
