Лабораторная работа n 3. Исследование переходных процессов синхронного двигателя

1. Цель работы

1.1. Изучение математической модели синхронного двигателя и реализация её в Simulink MATLAB.

1.2. Исследование с помощью математической модели переходных процессов синхронного двигателя.

2. Программа и указания к выполнению работы

2.1 Описание математической модели

Для анализа переходных процессов и исследования статической и динамической устойчивости синхронных машин удобно использовать систему координатных осей

d , q , неподвижных относительно ротора.

Для идеализированного синхронного двигателя с явновыраженными полюсами, оснащённого как обмоткой возбуждения, так и пусковой обмоткой, система уравнений электрического равновесия имеет вид

(1)

где u_d , u_q , i_d , i_q , ψ_d , ψ_q – напряжения, токи и потокосцепления обмоток якоря по осям d и q ; r – активное сопротивление фазы обмотки якоря; u_e , i_e , ψ_e , r_e – величины напряжения, тока, потокосцепления и активного сопротивления обмотки возбуждения, приведенные к обмотке якоря; i_pd , i_pq , ψ_pd , ψ_pq , r_pd , r_pq – токи, потокосцепления и активные сопротивления пусковой обмотки по осям d и q ; ω_r – угловая скорость ротора в электрических радианах в секунду; t – время; p – оператор дифференциирования.

Система уравнений электрического равновесия (1) справедлива как для поименованных, так и относительных величин. Система уравнений потокосцеплений для относительных величин может быть представлена в виде:

(2)

где x_d , x_e , x_pd , x_q , x_pq – полные индуктивные сопротивления обмотки якоря, обмотки возбуждения и пусковой обмотки по осям d и q; x_ad и x_aq – индуктивные сопротивления взаимной индукции по осям d и q;

У равнение электромагнитного момента в системе относительных велич имеет вид

(3)

У равнение механического равновесия для системы относительных величин записывается в виде

(4)

где J – приведенный к ротору момент инерции; M_s – момент механической нагрузки на валу двигателя.

При симметричном питании составляющие напряжения якоря по осям d и q в относительных величинах могут быть представлены в виде

(5)

где U – относительная величина напряжения питания. Для номинального напряжения U = 1; θ – угол нагрузки.

Зависимость между ω_r и θ в системе относительных единиц определяется выражением

(6)

Уравнения (1) – (6) составляют математическую модель синхронного двигателя. После преобразования математической модели в форму, удобную для моделирования в Simulink MATLAB, система уравнений математической модели принимает вид

(7)

Где коэффициенты в выражениях для токов определяются по формулам

(8)

Для номинального режима напряжение возбуждения и поток обмотки возбуждения в относительных величинах могут быть рассчитаны по формулам

(9)

Схема математической модели, реализованная в Simulink MATLAB, представлена на рисунке 1.

На схеме блоки F1, S1 и I1 реализуют решение 1-го уравнения системы(7), а блоки F2,S2 и I2 – решение 2-го уравнения системы, вырабатывая на выходе потокосцепления обмотки якоря по продольной Y_d и поперечной Y_q оси. Блоки S3 и I3 решают 3-е уравнение системы (7) и вырабатывают на выходе потокосцепление обмотки возбуждения Y_e . Блок U_e воспроизводит напряжение питания обмотки возбуждения . На схеме он отсоединён, что соответствует задаче запуска синхронного двигателя асинхронным пуском без возбуждения. Блоки I4 и I5 воспроизводят решение 5-го и 6-го уравнения системы (7) и вырабатывают соответственно потокосцепления пусковой обмотки по продольной Y_pd и поперечной Y_pq осям. Блоки S7, S8, S9, S10 и S11 , используя полученные потокосцепления, решают уравнения для токов(6-e – 10-e уравнения системы (7)). Блоки P3,P4 и S6 решают уравнение11 системы (7) т.е. уравнение электромагнитного момента. Блоки S4, K6 и I6 решают уравнение движения (12-е в системе (7)), вырабатывая на выходе скорость вращения ротора ω_r. Блоки ω_s, S5 и I7 решают уравнение 13 системы (7). На выходе блока S5 вырабатывается скольжение, а на выходе блока I7 вырабатывается угол нагрузки θ.

Рис.1. Схема моделирования синхронного двигателя

2.2. Исходные данные

Варианты исходных данных представлены в таблице 1.

Исходные данные Таблица 1

Nr вар	r* 103, о.е.	re* 103, о.е.	rpd, о.е.	rpq, о.е.	xd, о.е.	xq, о.е.	xe, о.е.	xad, о.е.	xaq, о.е.	xpd, о.е.	xpq, о.е.	J, о.е.
1	2	3	4	5	6	7	8	9	10	11	12	13
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16	32.1 28.4 21.7 24.0 39.8 20.7 16.9 33.7 23.8 18.9 19.8 24.5 32.4 30.8 29.1 31.7	6.78 5.81 4.05 5.41 3.03 5.64 2.92 7.22 4.74 2.52 3.48 5.99 6.25 6.58 5.49 5.54	0.207 0.133 0.113 0.132 0.124 0.100 0.098 0.166 0.123 0.0950.091 0.104 0.140 0.151 0.146 0.139	0.084 0.056 0.056 0.059 0.059 0.054 0.049 0.087 0.061 0.046 0.046 0.055 0.069 0.0690.076 0.061	1.189 1.412 1.236 1.1511.287 1.656 1.244 1.632 1.545 1.347 1.421 1.598 1.632 1.395 1.609 1.191	0.741 0.877 0.759 0.729 0.811 0.886 0.766 0.963 0.939 0.825 0.822 0.906 0.926 0.807 0.921 0.736	1.331 1.592 1.376 1.327 1.429 1.806 1.409 1.734 1.702 1.477 1.571 1.754 1.745 1.552 1.745 1.350	1.110 1.319 1.128 1.056 1.187 1.584 1.153 1.548 1.425 1.232 1.357 1.503 1.553 1.312 1.526 1.117	0.663 0.784 0.651 0.634 0.711 0.814 0.675 0.879 0.819 0.710 0.758 0.811 0.847 0.724 0.838 0.662	1.229 1.470 1.217 1.192 1.320 1.674 1.281 1.657 1.522 1.364 1.431 1.622 1.651 1.419 1.628 1.202	0.7090.844 0.694 0.691 0.771 0.859 0.736 0.934 0.867 0.771 0.794 0.871 0.893 0.770 0.889 0.699	143.7 162.3 293.1 207.3 247.5 219.2 284.4 255.3 253.3 276.8 287.8 232.8 166.3 194.6 209.1 218.2

2.3. Подготовка задачи.

Подготовка задачи заключается в расчёте параметров и передаточных коэффициентов математической модели синхронного двигателя. Ниже приведен пример подготовки задачи для 16-го варианта исходных данных.

2.3.1. Расчёт параметров модели.

Индуктивные сопротивления рассеяния обмотки якоря, обмотки возбуждения и пусковой обмотки по осям d şi q

(10)

2.3.2. Расчёт коэффициентов математической модели

2.3.3. Передаточные коэффициенты

K1 = K2 = r = 0.0317; K3 = r_e = 5.54*10 ^-3; K4 = -r_pd = -0.139;

K5 = -r_pq = -0.061 ; K6 = 1/J = 1/218.2 ; K71 = K_d = 7.551;

K72 = K92 = K_d1 = 1.916 ; K73 = K102 = K_d2 = 5.235; K81 = K_q = 9.253;

K82 = K112 = K_q1 = 8.769; K91 = K_e = 3.695;K93 = K103 = K_d3 = 1.653;

K101 = K_pd = 7.232;K111 = K_pq = 9.741.

2.4. Подготовка модели и выполнение исследований

Подготовка модели заключается в установке рассчитанных параметров в соответствующих блоках.

Исследования заключаются в снятии осциллограмм процесса пуска – зависимостей электромагнитного момента и скорости вращения ротора от времени M_eм(t) и ω_r(t) для 3-х случаев:

1. Обмотка возбуждения отключена от источника питания и закорочена накоротко;

2. Обмотка возбуждения подключена к источнику питания;

3. Обмотка возбуждения отключена от источника питания и её сопротивление увеличено в 10 раз.

Примеры снимаемых осциллограмм приведены на рисунках Рис.2 – Рис.4.

Рис.2. Осциллограмма процесса пуска синхронного двигателя в возбуждённом состоянии (обмотка возбуждения подключена к источнику питания).

Зависимости M_em(t), ω_r(t).

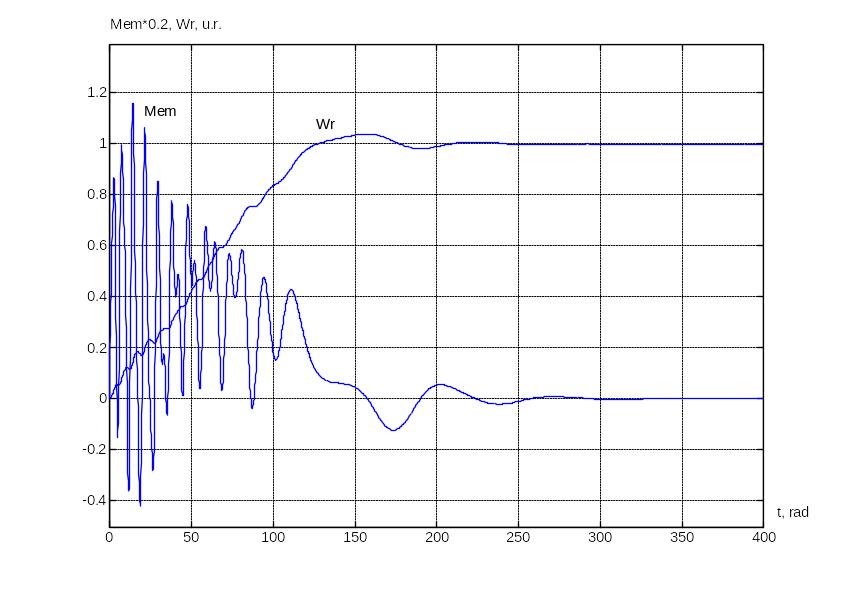
Рис.3. Осциллограмма процесса пуска при закороченной

накоротко обмотке возбуждения. Зависимости M_em(t), ω_r(t).

Рис.4. Осциллограмма процесса пуска при отключённом питании обмотки возбуждения и увеличенном в10 раз сопротивлении обмотки возбуждения.

Зависимости M_em(t), ω_r(t).

3. Содержание отчёта

Отчёт должен содержать следующие разделы:

• Исходная математическая модель

• Схема моделирования

• Расчёт необходимых параметров и передаточных коэффициентов модели

• Снятые осциллограммы

• Анализ результатов и выводы

4. Контрольные вопросы

1. Как влияет подключение обмотки возбуждения на процесс асинхронного пуска синхронного двигателя?

2. В чём разница между статической и динамической устойчивостью синхронной машиныÎn?

3. Как влияет величина тока возбуждения на угловую характеристику синхронной машины?

4. Как влияет конструкция ротора синхронной машины на её параметры?