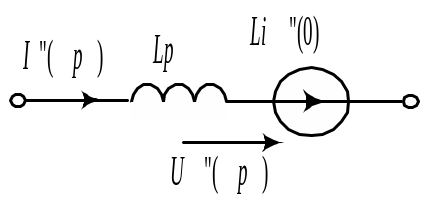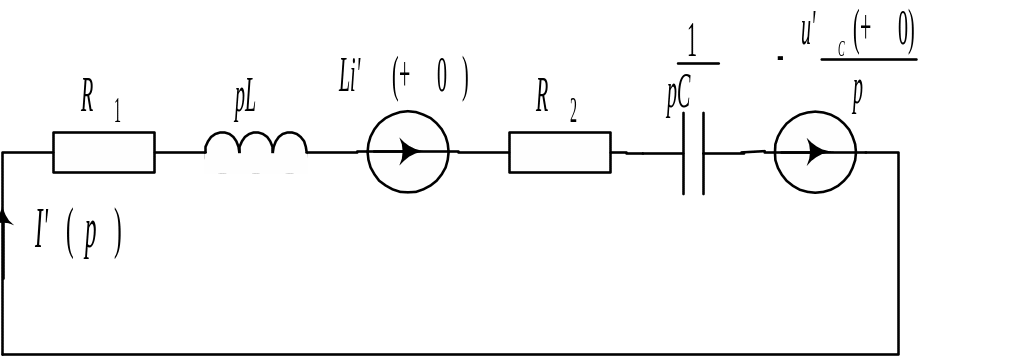- •Глава 9
- •9.1.2. Преобразование Лапласа
- •9.1.3. Основные свойства преобразования Лапласа
- •9.2. Законы Ома и Кирхгофа в операторной форме
- •9.2.1. Закон Ома
- •9.2.2. Первый закон Кирхгофа
- •9.2.3. Второй закон Кирхгофа
- •9.3. Теорема разложения
- •9.4. Методика расчета переходных процессов операторным методом
- •9.4.1. Порядок расчета операторным методом
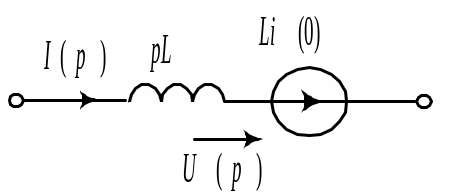
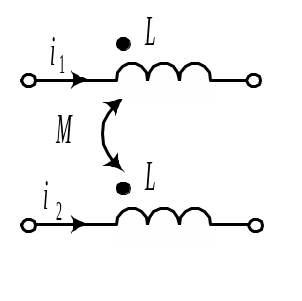
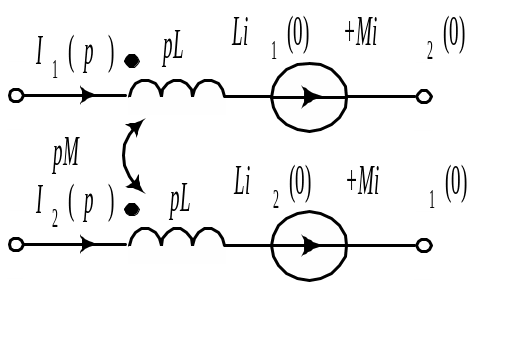
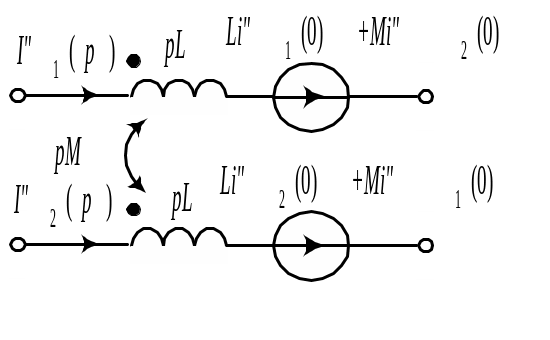
- •9.4.2. Операторные схемы замещения идеальных элементов
- •9.4.3. Особенности расчёта переходного процесса в цепи с гармоническими источниками
- •9.4.4. Расчёт операторным методом свободной составляющей
- •9.5. Примеры расчета переходных процессов операторным методом
- •1. Установившийся режим до коммутации и независимые начальные условия:
- •Контрольные вопросы
9.5. Примеры расчета переходных процессов операторным методом
Пример 9.3
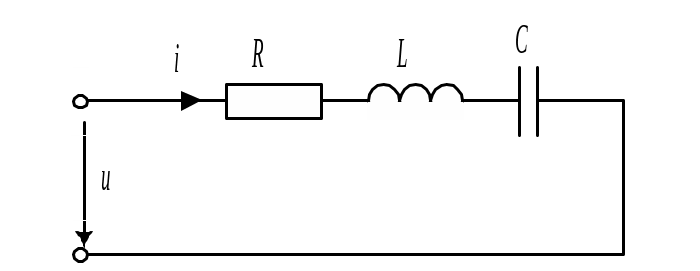
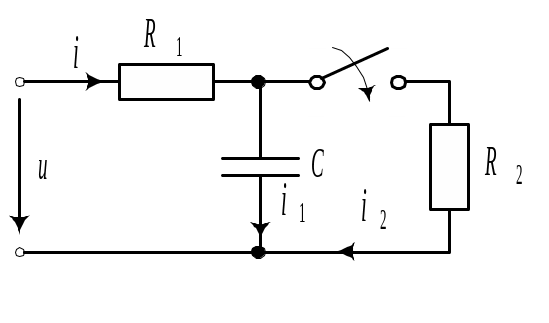
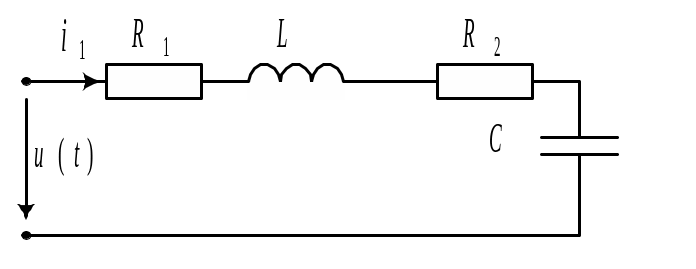
Составить операторную схему замещения для переходного режима в цепи (рис. 9.6) при ненулевых начальных условиях.
|
|
Рис. 9.6 |
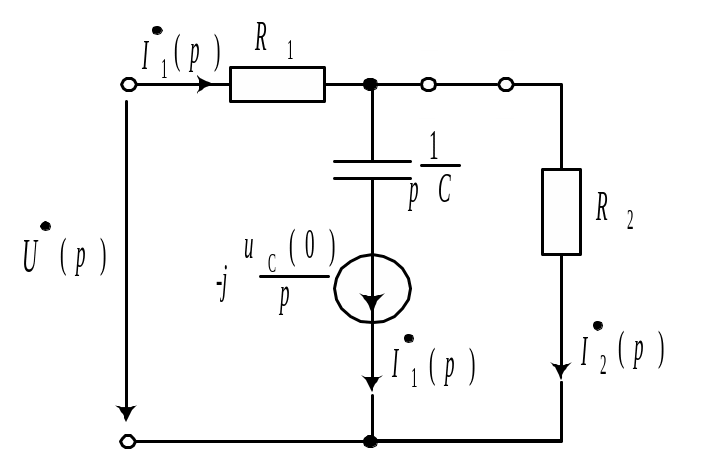
Рис. 9.7 |
Таблица 9.2
Элемент |
Схема замещения |
|
Для свободной и принужденной составляющих |
Для свободной составляющей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение
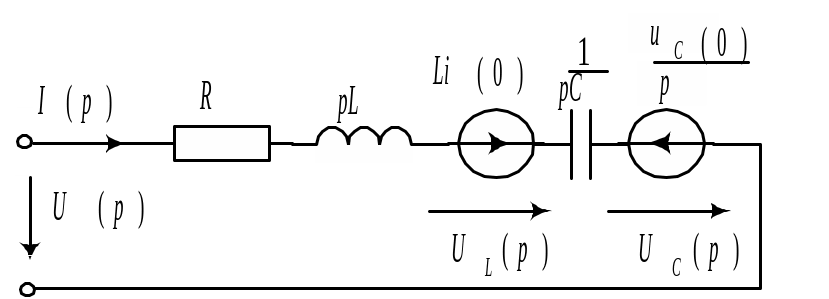
Согласно табл. 9.2 в операторной схеме
замещения резистор заменяется операторным
сопротивлением
![]() ,
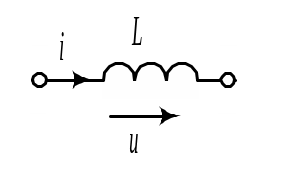
катушка – операторным сопротивлением
,
катушка – операторным сопротивлением
![]() и э.д.с.
и э.д.с.
![]() ,
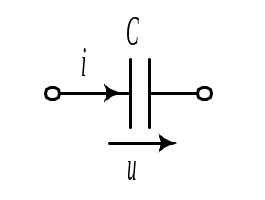
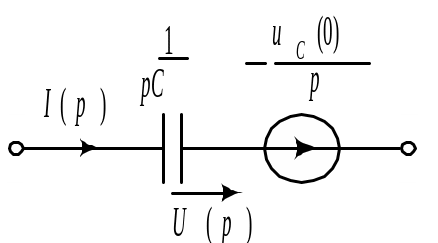
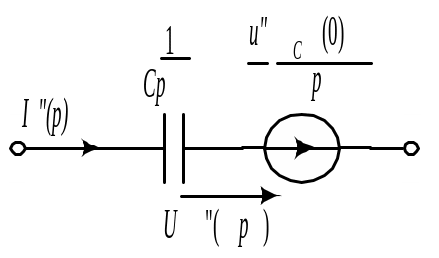
конденсатор – операторным сопротивлением
,
конденсатор – операторным сопротивлением
![]() и э.д.с.
и э.д.с.
![]() .
Операторная схема замещения показана
на рис. 9.7.
.
Операторная схема замещения показана
на рис. 9.7.
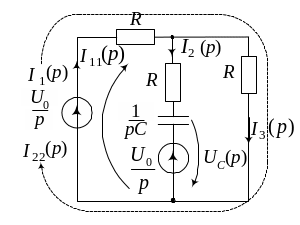
Пример 9. 4. Найти операторное изображение напряжения на конденсаторе в схеме, показанной на рис. 9.8.
Решение
1. Установившийся режим до коммутации и независимые начальные условия:
|
|
Рис. 9.8 |
Рис. 9.9 |
2. Операторное
изображение постоянного напряжения
![]() .
.
3. Операторная схема замещения показана на рис. 9.9. Расчёт операторной схемы выполним методом контурных токов:
![]()
Откуда
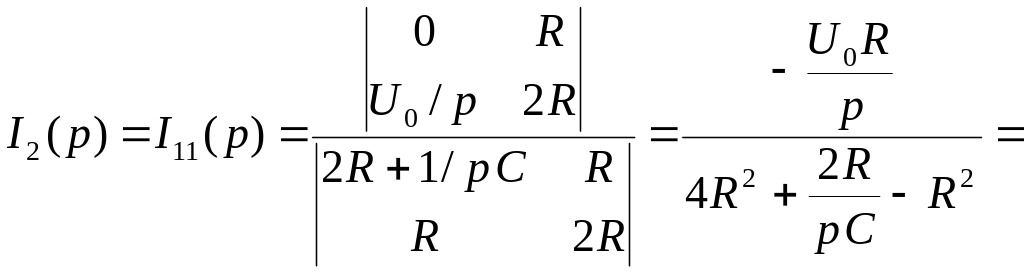
![]()
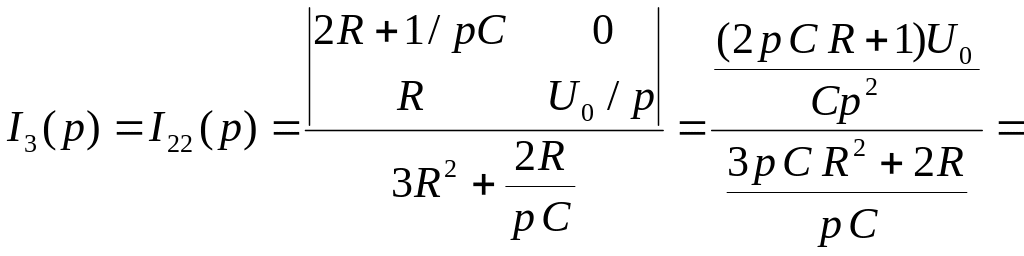
![]()
![]()
Конденсатор на операторной схеме
представлен двумя элементами. Для
расчёта
![]() лучше рассмотреть контур, в уравнение
для которого входит изображение
(см. рис. 9.9). Тогда получаем
лучше рассмотреть контур, в уравнение
для которого входит изображение
(см. рис. 9.9). Тогда получаем
![]()
![]()
![]() .
.
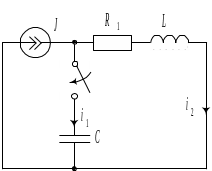
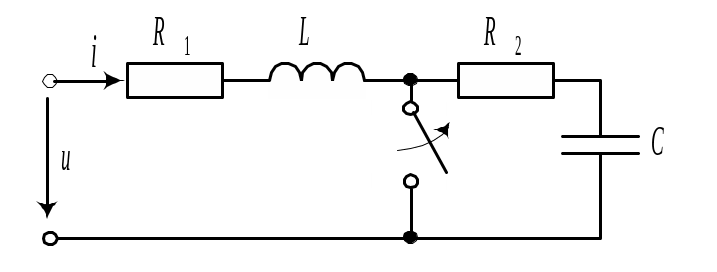
Пример 9.5
Рассчитать операторным методом токи в
ветвях схемы, показанной на рис. 9.9. В
схеме действует идеальный источник
постоянного тока
![]() А. Параметры элементов:
А. Параметры элементов:
![]() Ф;
Ф;
![]() Гн;
Гн;
![]() Ом.
Ом.
|
|
Рис. 9.10 |
Рис.9.11 |
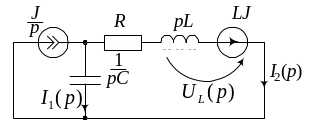
Решение
Независимые начальные условия:
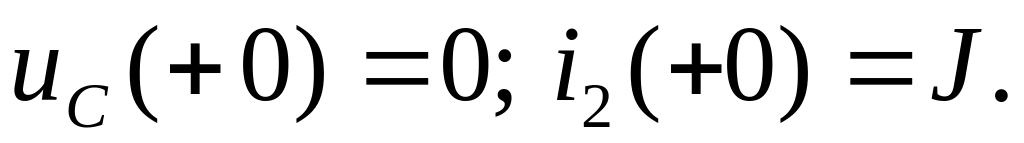
2. Операторное изображение задающего
тока
![]() .
.
3. Операторная схема приведена на рис. 9.11. Её расчёт выполним по уравнениям Кирхгофа:
![]() ;
;
![]() ;
;
![]()
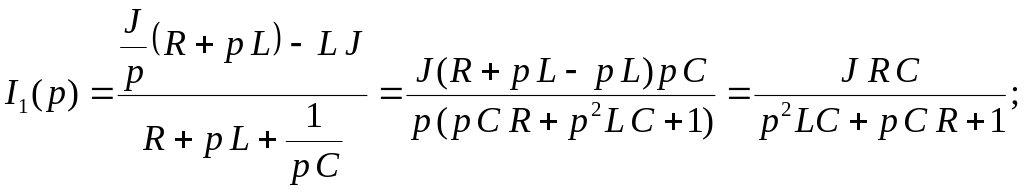
![]()
![]()
Катушка индуктивности представлена её
операторным сопротивлением и э.д.с
начальных условий. Для определения
![]() запишем уравнение по второму закону
Кирхгофа для указанного на схеме контура:
запишем уравнение по второму закону
Кирхгофа для указанного на схеме контура:
![]() ,
,
откуда
![]()
![]()
Дальнейший расчёт выполним в цифрах:
![]()
![]()
![]()
![]() ;
;
![]() .
.
4. Переход к оригиналам выполним по
теореме разложения. Для выбора модификации
теоремы разложения определим корни
многочлена знаменателя, т.е. решим
уравнение
![]() .
Корни
.
Корни
![]()
![]()
![]() Все корни простые, поэтому можно
воспользоваться формулой (9.17). У
знаменателя
Все корни простые, поэтому можно
воспользоваться формулой (9.17). У
знаменателя
![]() выражения для
выражения для
![]() два корня, следовательно
два корня, следовательно
![]() ,
,
где
![]()
![]() ;
;
![]() ;
;
![]() ,
,
тогда
![]() А;
А;
![]() А.
А.
Знаменатель
функции
![]() имеет ещё третий нулевой корень, тогда
имеет ещё третий нулевой корень, тогда
![]() ,
,
где
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
В результате получаем
![]() В.
В.
Напряжение на катушке и источнике
![]() ,
,
где
![]() ;
;
![]() .
.
В результате
![]() В.
В.
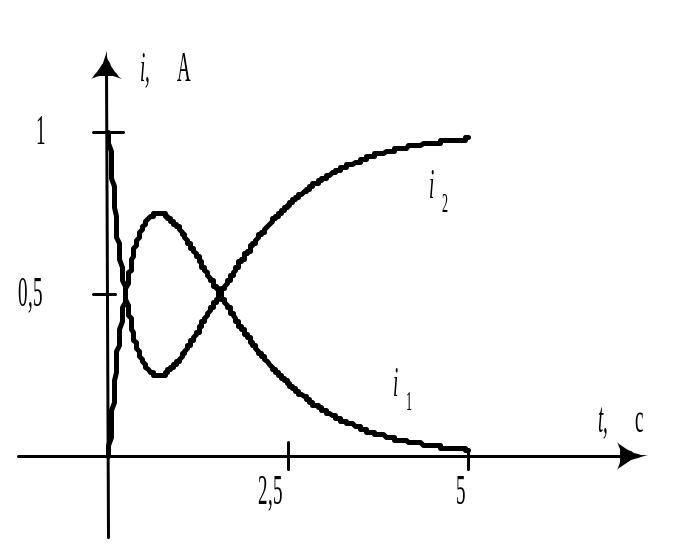
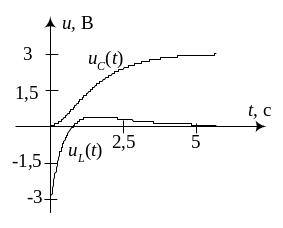
Графики зависимостей токов в ветвях показаны на рис. 9.12,а, а напряжений на катушке и конденсаторе – на рис. 9.12,б.
а) |
|
б) |
|
Рис. 9.12 |
|||
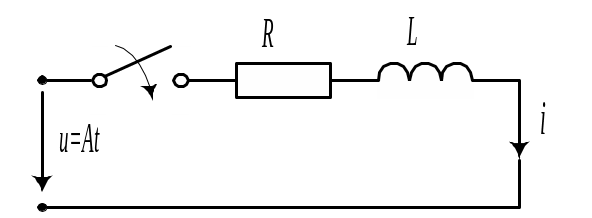
Пример 9.6
В схеме, изображенной на рис. 9.13 рассчитать
ток
![]() операторным методом.
операторным методом.
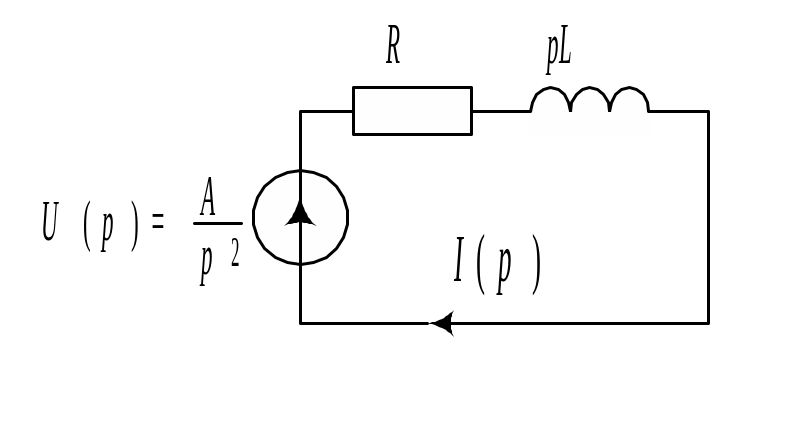
|
|
Рис. 9.13 |
Рис. 9.14 |
Решение
Изображение входного напряжения
 (см. таблицу 9.1). Начальные условия –
нулевые.
(см. таблицу 9.1). Начальные условия –
нулевые.Операторная схема показана на рис. 9.14. Операторное изображение тока
![]()
3. Переход к оригиналу выполним по теореме
разложения. Корни знаменателя
![]() :
:
![]()
![]()
Если знаменатель имеет
![]() простых
простых
![]() корней и корень
корней и корень
![]() кратности
кратности
![]() (
одинаковых корней), то теорема разложения
записывается в виде (9.19). В частности
при двух одинаковых корнях
(
одинаковых корней), то теорема разложения
записывается в виде (9.19). В частности
при двух одинаковых корнях
![]() выражение (9.19) имеет вид
выражение (9.19) имеет вид
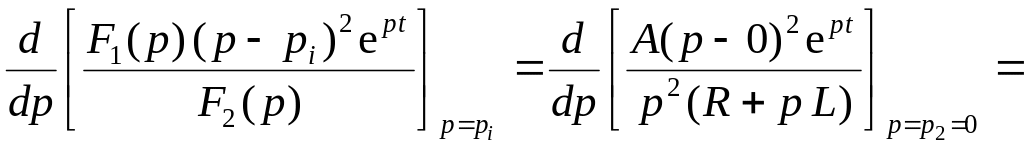
![]()
Для простого корня согласно теореме разложения
![]() .
.
Объединяя составляющие, получим искомый ток
![]()
Переход
![]() можно выполнить по таблице 9.1.
можно выполнить по таблице 9.1.
Пример 9.7
Требуется определить закон
изменения напряжения на конденсаторе
для цепи, изображенной на рис. 9.15. К цепи
приложено синусоидальное напряжение
![]() параметры элементов цепи:
параметры элементов цепи:
![]() мкФ;
мкФ;
![]() Ом. При расчете использовать комплексное
изображение синусоидального напряжения.
Ом. При расчете использовать комплексное
изображение синусоидального напряжения.
Решение
1. Расчёт установившегося режима до коммутации осуществляется символическим методом:
![]() В;
В;
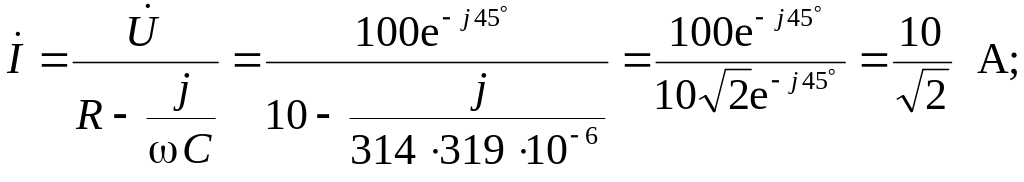
![]()
|
|
Рис. 9.15 |
Рис. 9.16 |
Тогда мгновенное значение напряжения на конденсаторе
![]()
и согласно
законам коммутации
![]() .
.
2. Операторная схема для комплексных изображений токов и напряжений показана на рис. 9.16. Операторное изображение источника в комплексной форме имеет вид
![]()
Расчет операторной схемы проведем по методу узловых потенциалов:
![]()
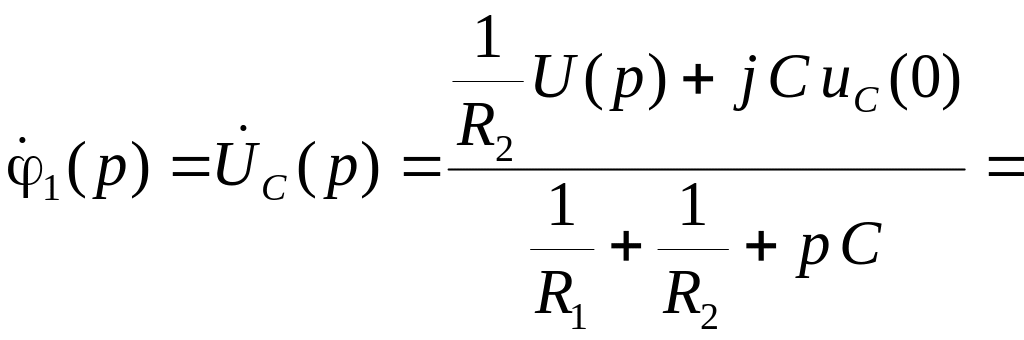
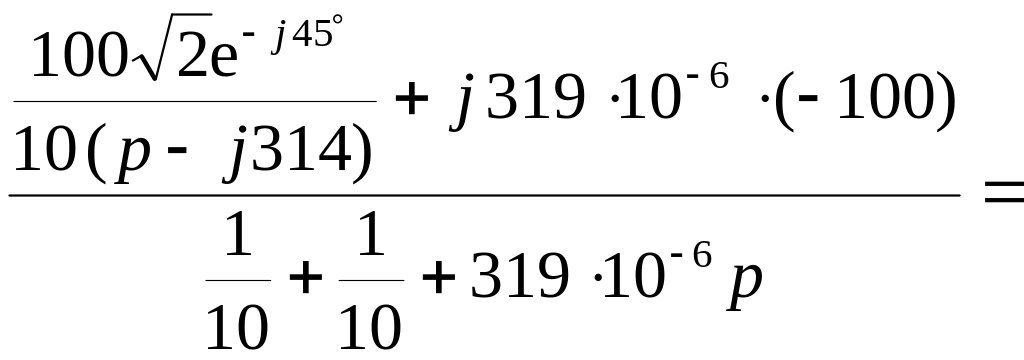
![]()
![]()
Для нахождения комплекса мгновенного значения напряжения на конденсаторе используем теорему разложения.
Корни многочлена в знаменателе
![]() или
или
![]() :
:
![]() c–1;
c–1;
![]() c–1.
c–1.
Производная знаменателя
![]()
По теореме разложения определяем комплекс мгновенного значения напряжения на конденсаторе:
![]()
![]()
![]()
![]()
![]()
Тогда мгновенное значение напряжения на конденсаторе:
![]()
Пример 9.8
Найти ток в катушке
индуктивности для цепи, изображенной
на рис. 9.17. К цепи приложено синусоидальное
напряжение
![]() В. Параметры элементов:
В. Параметры элементов:
![]() ;
;
![]() ;
;
![]() ;
;
![]() мкФ.
мкФ.
|
|
Рис. 9.17 |
Рис. 9.18 |
Рубильник отключается в момент прохождения тока через максимальное значение.
Решение
1. Расчёт установившегося режима до коммутации в цепи на рис. 9.18 выполним символическим методом:
![]() ;
;
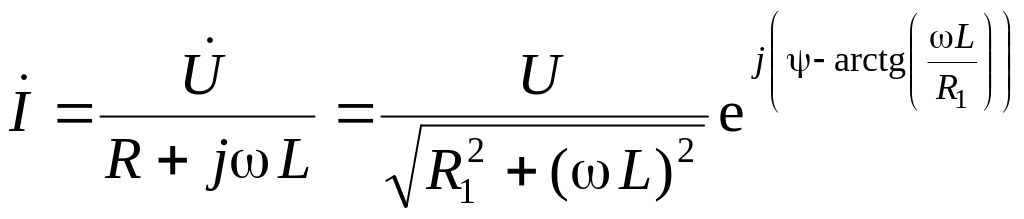 .
.
Тогда мгновенное значение тока
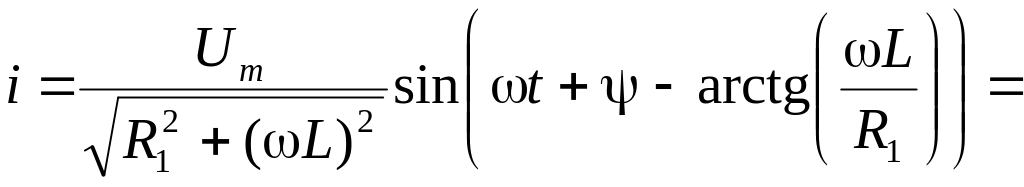
![]()
![]()
Поскольку коммутация происходит при
максимальном значении тока, то начальная
фаза тока
![]() ,
откуда
,
откуда
![]() При этом значение тока
При этом значение тока
![]() в момент коммутации, согласно выражению
в момент коммутации, согласно выражению
![]() ,
,
![]()
2. Расчёт установившегося режима после коммутации также выполним символическим методом (см. цепь на рис. 9.19):
![]() В;
В;
![]() Ом;
Ом;
![]() А;
А;
![]() В.
В.
Тогда мгновенные значения тока и напряжения на конденсаторе:
![]()
![]()
Определение начальных условий для свободных составляющих:
![]() ;
;
![]() ;
;
![]() ;
;
![]()
4. Эквивалентная операторная схема для свободных составляющих показана на рис. 9.20.
|
|
Рис. 9.19 |
Рис. 9.20 |
Операторное изображение свободной составляющей тока
![]() .
.
Корни
многочлена знаменателя
![]() :
:
![]()
![]()
![]()
Переход от изображений к оригиналам выполним по теореме разложения. Свободная составляющая тока:
![]()
![]()
![]()
![]()
![]()
![]()
![]() А.
А.
Выражение для тока в цепи запишем как сумму свободной и принуждённой составляющих тока:
![]() А.
А.