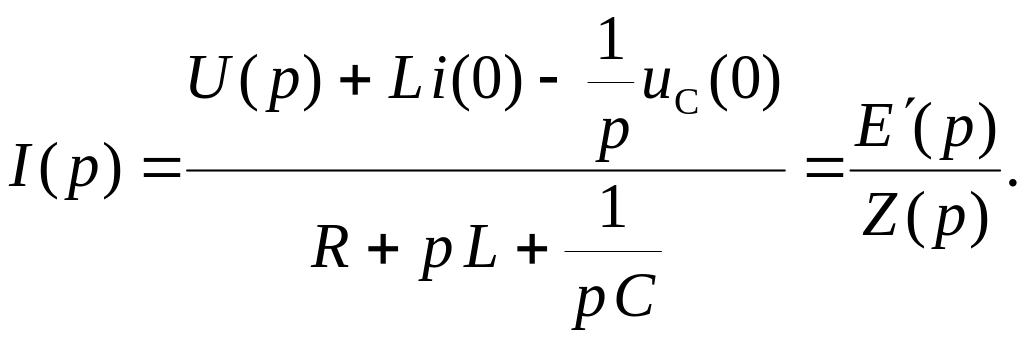9.1.3. Основные свойства преобразования Лапласа

1. При умножении оригинала на постоянную величину на ту же постоянную величину умножается и изображение:

2. Если оригинал представлен суммой функций, то изображение этой суммы равно сумме изображений этих функций:

(9.3)

Доказательство выражения (9.3) вытекает непосредственно из свойств определённого интеграла

.

3. Изображение производной.

Пусть дана некоторая функция и известно её изображение F(p). Тогда изображение Ф(p) производной этой функции :

.

Интегрируя по частям при и ( ; ) и используя условие существования интеграла Лапласа: , получаем

.

Итак, изображение производной имеет вид

(9.4)

где – значение функции при . Согласно (9.4) вычисление изображения производной функции при нулевых начальных условиях ( ) соответствует умножению изображения функции на оператор .

Используя формулу (9.4), можно найти изображение второй производной оригинала:

или

Повторяя эти вычисления раз, получим изображение производной оригинала го порядка:

(9.5)

где

.

В выражении (9.5) и все её производные до включительно непрерывны.

Если начальные значения функции и всех её производных равны нулю, то изображение производных, определяемых уравнением (9.5), упрощается и находится по изображению исходной функции простым умножением на оператор в степени, соответствующей порядку производной:

4. Изображение интеграла.

Пусть дана некоторая функция и известно её изображение . Необходимо найти изображение интеграла от этой функции

Так как и =0, то Учитывая, что изображение функции равно получаем Таким образом, окончательно имеем:

(9.6)

Согласно (9.6) интегрированию функции в пределах от 0 до t соответствует деление изображения этой функции на оператор p. При многократном интегрировании в пределах от 0 до t можно получить общее выражение:

(9.7)

где n – любое целое число.

Приведём также некоторые теоремы, которые могут быть использованы при расчётах электротехнических задач.

5. Теорема подобия.

Изменение масштаба независимого переменного осуществляется согласно выражению

6. Теорема запаздывания.

Смещение в области действительного переменного на время равносильно умножению изображения на :

.

7. Теорема смещения.

Смещение в области комплексной переменной p на величину равносильно умножению оригинала на показательную функцию :

.

8. Теорема свертывания.

Теорема свертывания в области действительной переменной име-

ет вид:

Умножение в области действительного переменного соответствует свёртыванию в области комплексного переменного (следствие теоремы свёртывания)

.

9.2. Законы Ома и Кирхгофа в операторной форме

9.2.1. Закон Ома

Рассмотрим процесс подключения последовательной цепи из иде-

	альных элементов R, L, C к источнику напряжения (рис. 9.1). Будем предполагать, что конденсатор был предварительно заряжен до напряжения . По второму закону Кирхгофа для данной цепи
Рис. 9.1
		(9.8)

Величины, входящие в уравнение (9.8) имеют изображения:

; ;

.

Используя свойство (9.3) преобразования Лапласа запишем уравнение (9.8) в операторной форме:

Откуда

(9.9)

Выражение (9.9) является законом Ома в операторной форме. В выражении (9.9):

– операторное сопротивление;

– э.д.с. начальных условий;

– суммарная э.д.с. ветви.

Операторное сопротивление имеет такую же структуру как и комплексное сопротивление , только вместо стоит оператор . Выражение (9.9) отличается от закона Ома в комплексной форме только тем, что в числителе, помимо э.д.с., включённой в ветвь, стоят ещё э.д.с. и , которые называют э.д.с. начальных условий. Эти э.д.с. учитывают, что в момент коммутации (при ) магнитное поле катушки и электрическое поле конденсатора обладали определённым запасом энергии. Переходный процесс будет определяться этим запасом энергии. Таким образом, начальные условия учитываются непосредственно в уравнениях цепи в виде э.д.с. и . В этом заключается преимущество операторного метода перед классическим.

При нулевых начальных условиях закон Ома в операторной форме имеет совершенно ту же структуру, что и в комплексной форме: