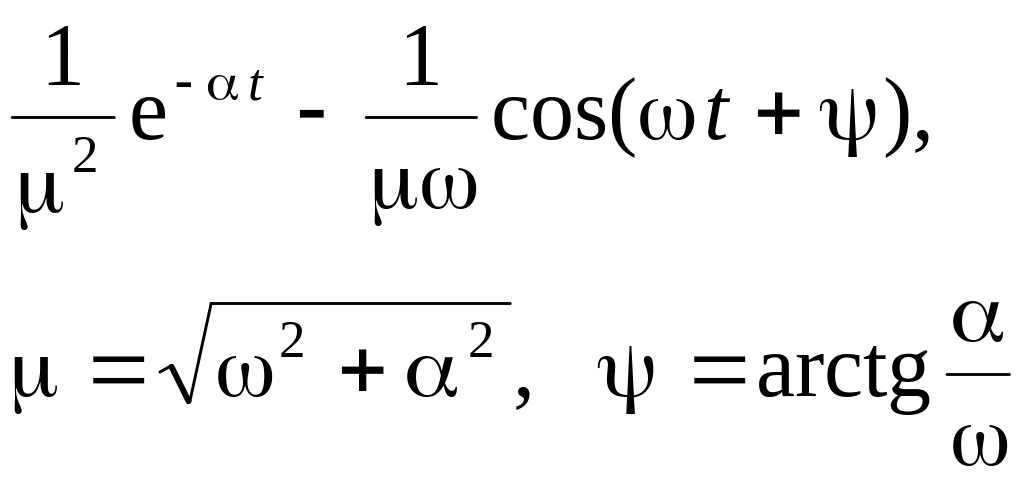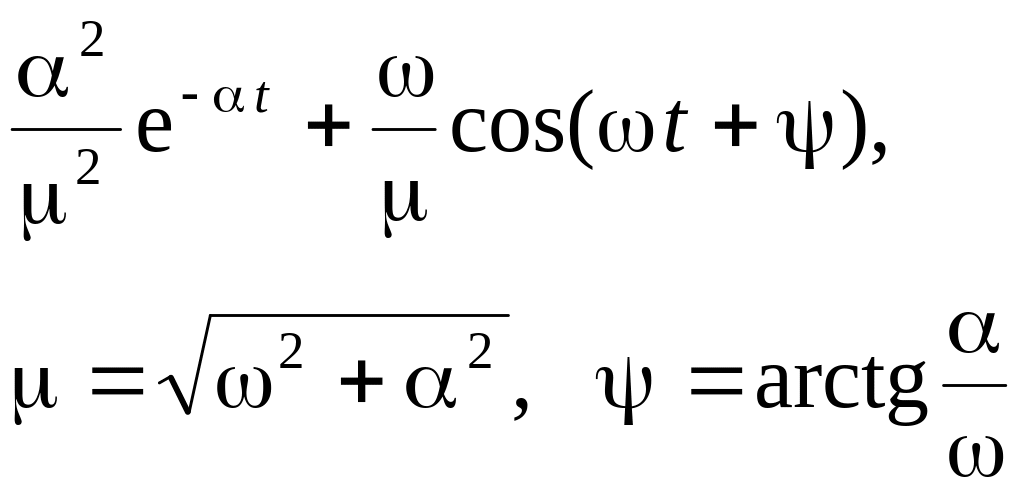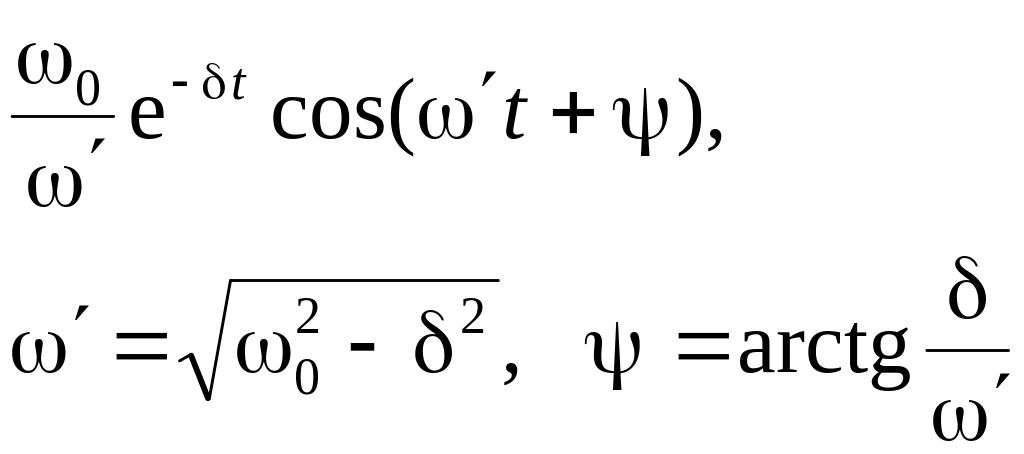Глава 9

ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ

ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

9.1. Основные положения операторного метода

9.1.1. Сущность метода

Расчёт переходных процессов классическим методом сводится к решению дифференциальных уравнений. При этом основные трудности решения заключаются в определении постоянных интегрирования. По мере усложнения электрической цепи и повышения порядка дифференциального уравнения эти трудности увеличиваются. Избежать этого позволяет операторный метод интегрирования линейных дифференциальных уравнений.

В электротехнику операторный метод в конце прошлого столетия ввёл О. Хевисайд. В настоящее время этот метод находит широкое применение в различных областях: энергетике, радиотехнике, связи и т.д.

Сущность метода заключается в следующем.

Заданную функцию действительного переменного (например, времени) преобразуют в функцию комплексного переменного , где . При этом исходную функцию называют оригиналом, а его изображением.

Дифференциальные уравнения для оригиналов, согласно правилам преобразования функций, их производных и интегралов, преобразуют в операторные алгебраические уравнения для изображений. Полученные операторные уравнения решают относительно функции комплексного переменного . Затем осуществляют переход от функции комплексного переменного к оригиналу .

Таким образом, сложные математические операции решения дифференциальных уравнений заменяются решением простых алгебраических уравнений, записанных в операторной форме. Операторный метод можно сравнить с логарифмированием, где сначала от чисел переходят к их логарифмам, потом производят относительно простые действия над логарифмами, соответствующие действиям над числами, а затем от найденного логарифма возвращаются к некоторому числу. При использовании комплексного метода расчёта установившегося режима в цепях синусоидального тока мы также применяем изображение синусоидальной функции функцией комплексной переменной.

Для преобразования функции вещественной переменной в функцию комплексной переменной пользуются преобразованием Лапласа.

9.1.2. Преобразование Лапласа

Пусть задана некоторая функция времени , удовлетворяющая условиям Дирихле:

1. за любой конечный промежуток времени имеет конечное число разрывов первого рода (нигде не превращается в бесконечность);

2. возрастает не быстрее показательной функции (существует постоянное число , такое, что для всех t ).

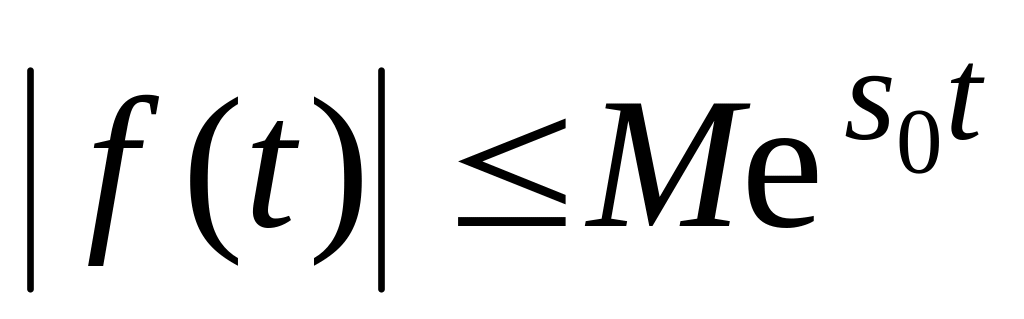Практически все функции, описывающие переходные процессы в реальных линейных электрических цепях, удовлетворяют этим условиям.

Преобразование вида

(9.1)

носит название преобразования Лапласа.

Оказывается, что если функция удовлетворяет перечисленным условиям Дирихле, то несобственный интеграл сходится, т.е. имеет конечное значение. В выражении (9.1): е – основание натурального логарифма; (  – новая переменная. Интеграл (9.1) используется для перехода от оригинала к изображению , причём сопоставление этих функций получается однозначным.

Существует обратное функциональное преобразование, дающее возможность определить оригинал по его изображению . Такое преобразование, носящее название обратного преобразования Лапласа, имеет вид

(9.2)

Следует отметить, что между изображением и оригиналом нет равенства, а есть только соответствие. Это важное положение подчёркивается условной записью, связывающей изображение с оригиналом. В литературе встречаются следующие виды символов, связывающие оригинал с его изображением:

; ; ; и др.

Соответствие между оригиналом и изображением будем в дальнейшем записывать в таком виде: или .

Кроме преобразования Лапласа используется также преобразование Карсона-Хевисайда:

.

Преимущество преобразования по Карсону состоит в том, что размерности оригинала и его изображения одинаковы, что не имеет места в преобразовании по Лапласу. Тем не менее, будем пользоваться преобразованием Лапласа, так как оно тесно связано с преобразованием Фурье и может трактоваться как обобщение преобразования Фурье.

Пример 9.1

Найти операторное изображение по Лапласу функции

Решение

Используя (9.1) получаем

.

Если , то получаем Если и , то получаем Поскольку , то и

Пример 9.2

Найти операторное изображение по Лапласу для функции .

Решение

Операторное изображение функции имеет вид

.

Используя интегрирование по частям:

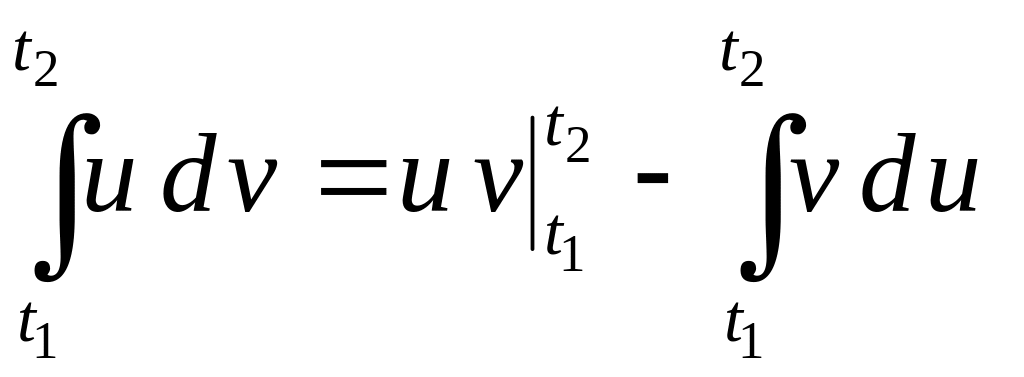
и обозначив и , имеем , ,

.

При подстановке верхнего предела в первое слагаемое получается неопределенность, раскрываемая по правилу Лопиталя:

.

Таким образом,

.

Изображения встречающихся в электротехнике функций уже рассчитаны. Они сведены в таблицы, имеющиеся в справочниках и специальной литературе. В таблице 9.1 приведены оригиналы и изображения наиболее часто встречающихся функций.

Таблица 9.1

№п.п.	Изображение	Оригинал
	1	2
1
2
3
4
5
6
7
8
9
10
11
	1	2
12
13
14
15
16
17
18
19
20
21