5.7. Методы покоординатного спуска.

5.7.1 Метод покоординатного спуска (Гаусса – Зейделя)

Необходимое условие существования экстремума функции многих переменных f(x₁,x₂,…,x_n)=f(x) равенство нулю частных производных в точке экстремума.

Градиенты функции обозначают f(x) или g(x). Тогда g(x)=0. В случае глобального максимума f(x)<f(x₀).

Точно также как и для функции одной переменной имеем:

• максимум, если вторая производная от f по х, т.е. G(x)-гессиан, отрицательно определен,

• минимум, если G(x) положительно определен.

Пример: (5.10)

Определяем градиент и приравниваем его нулю:

. Точка экстремума x₁=1 , x₂=2 , x₃=3.

- гессиан положительно определен, так как все собственные значения

положительны и равны 2. В точке (1,2,3) f(x) достигает минимума.

Таким образом, самый очевидный метод поиска экстремума многих переменных – это метод покоординатного спуска. Сначала любым из методов для функции одной переменной определяется экстремум функции относительно этой переменной. Затем переменная фиксируется и идет поиск экстремума по другой переменной и т.д. Из описания алгоритма метода следует, что шаг движения по координатам х задан Δх. Он обычно одинаков для всех координат х.

Когда найдено значение всех координат в точке экстремума (одна итерация), шаг уменьшается. Процесс итераций заканчивается, если изменение шага не приводит к изменению функции.

Метод эффективен для сепарабильных функций, у которых отсутствуют перекрестные связи между координатами. Если для получения решения требуется несколько итераций, то метод теряет свою эффективность.

Пример сепарабильной функции:

F(x)= F_i(x_i – x_i^*) , где F_i – унимодальные функции с минимумом в начале координат.

Графическая иллюстрация метода для одной итерации:

• найдены для достаточно малого шага

В процессе итераций значения должны совпасть.

На этом рисунке показаны линии равного уровня для функции двух переменных F(x , x) .

Приведем примеры функций, для которых применим метод покоординатного спуска.

1. F=x₁²+x₂²+x₃²

2. F= (x₁ –1)²+( x₂ - 2)²+( x₃-3)²=0

Программа метода покоординатного спуска.

Procedure COORD;

var I:integer; var E,B,C,L,H : real; label 1,2;

begin

H:=0.1; E:=1E-5; L:=H;

2: for I:=1 to N do

begin

B:=1E+38;

1: x[I]:=x[I]+H; FUNK; C:=B; B:=F;

if (F-C)<0 then goto 1;

H:=-H/3;

if abs(H)>=abs(L/3) then goto 2;

H:=L;

end;

L:=L/9; H:=L;

if E/9<=L then goto 1;

write(x);

end;

Число переменных N задано и описано в основной программе. Вектор Х должен быть задан по начальным приближениям Х⁰ и описан в основной программе.

Результат расчета процедуры FUNK должен содержаться в F. Входным параметром ее должен быть Х.

5.7.2. Метод спирального покоординатного спуска.

Разновидностью метода покоординатного спуска является метод спирального покоординатного спуска. При использовании этого метода шаг по координатам меняется при переходе от одной переменной к другой.

Программа метода спирального покоординатного спуска:

Procedure COORDS;

var I:integer; var B,C,N,E:real; label 1,2;

begin

H:=0.1; E:=1E-5;

2: for I:=1 to N do

begin

B:=1E+38;

1: x[I]:=x[I]+H; FUNK; C:=B; B:=F;

if (F-C)<0 then goto 1;

end;

H:=-H/5;

if abs(H)>abs(E/3) then goto 2;

write(x);

end;

Методы покоординатного спуска плохо работают, если функция имеет “овраг”, дно которого не сориентировано вдоль координатных осей.

На рис.5.10 показан такой вариант. Овраг не сориентирован вдоль координатных осей. Любое движение по осям координат не дает успеха,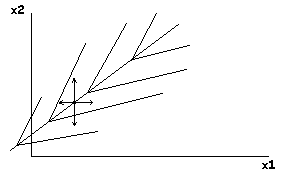 так как приводит к увеличению

функции. Для узкого и извилистого оврага проблемы поиска экстремума еще более осложняются.