3.1.Метод интерполяции Лагранжа.

Рассмотрим функцию , проходящую через точки :

(3.1)

См. рис. 3.1. Указанные в (3.1) функции называются коэффициентами полинома Лагранжа и формируются так:

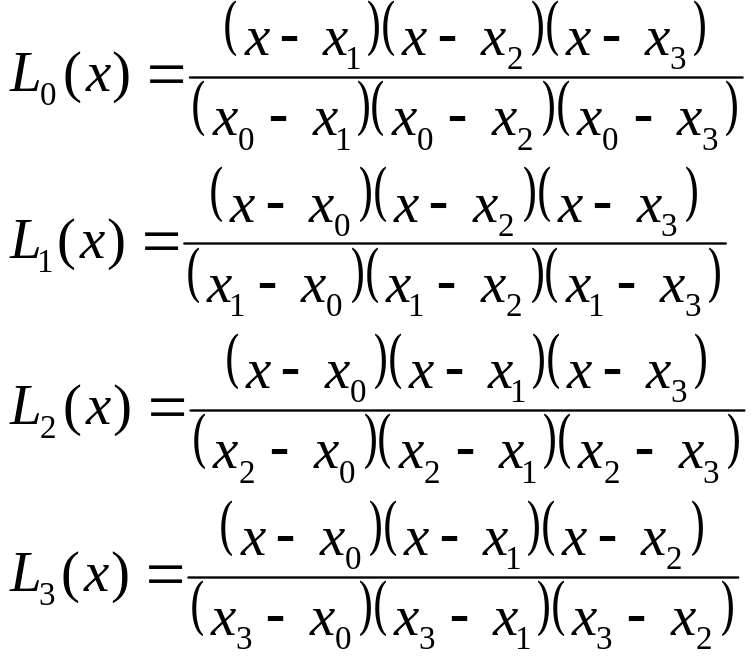
Рис. 3.1.

Легко оценить, что в узловых точках коэффициенты полиномов Лагранжа имеют следующие значения:

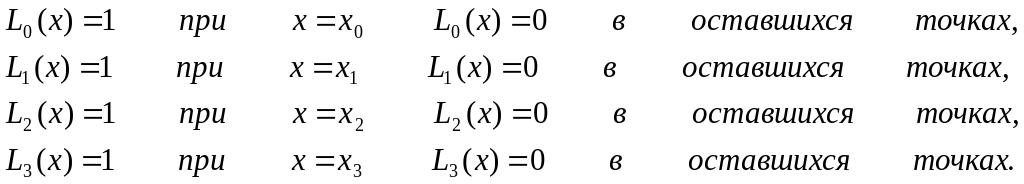Поэтому f(x) принимает в узловых точках значения f(x₀) , f(x₁), f(x₂), f(x₃).

В общем виде коэффициенты полинома можно записать так:

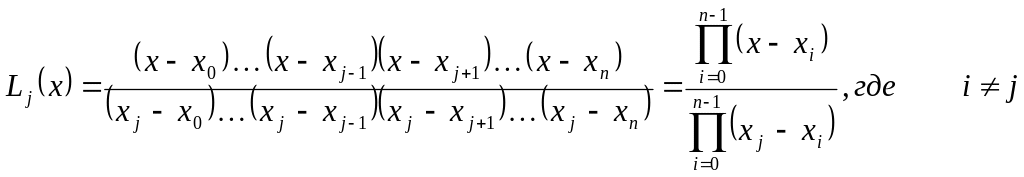
В общем виде функцию f(x) можно записать так: .

В коэффициентах полинома Лагранжа знаменатели содержат постоянные коэффициенты, которые легко определяются после разбивки интервала на узлы.

Приведем программу интерполяции методом Лагранжа.

function [C,L]=lagran(X,Y)

%Вектор абсцисс X

%Вектор ординат Y

%Вектор коэффициентов интерполирующего полинома С

%Матрица коэффициентов полинома Лагранжа L

%Обращение из МАTLAB: X=0:0.5:2; Y=exp(-X).*sin(3*X); [C,L]=lagran(X,Y)

w=length(X);

n=w-1;

L=zeros(w,w);

for k=1:n+1

V=1;

for j=1:n+1

if k~=j

V=conv(V,poly(X(j)))/(X(k)-X(j));

end

end

L(k,:)=V;

end

C=Y*L;

X=0:0.1:2;

Y=exp(-X).*sin(3*X);

Y1=C(1).*X.^4+C(2).*X.^3+C(3).*X.^2+C(4).*X;

plot(X,Y,X,Y1)

3.2.Интерполяционные полиномы Эрмита

При интерполяции полиномами Эрмита требуется выполнение двух условий:

в узловых точках должны совпадать значения функции и ее производной . ( ). Но постановка задачи сохраняется. Будем искать многочлены и такие, что при

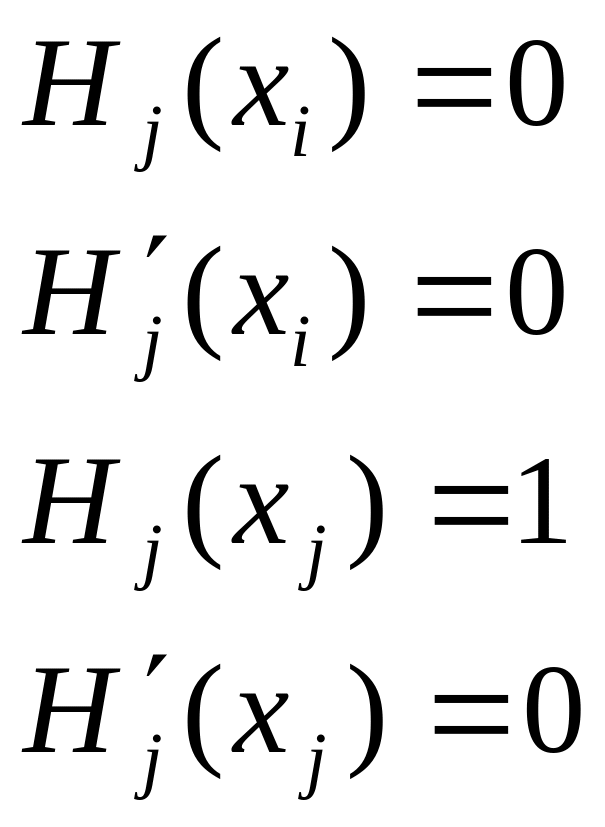
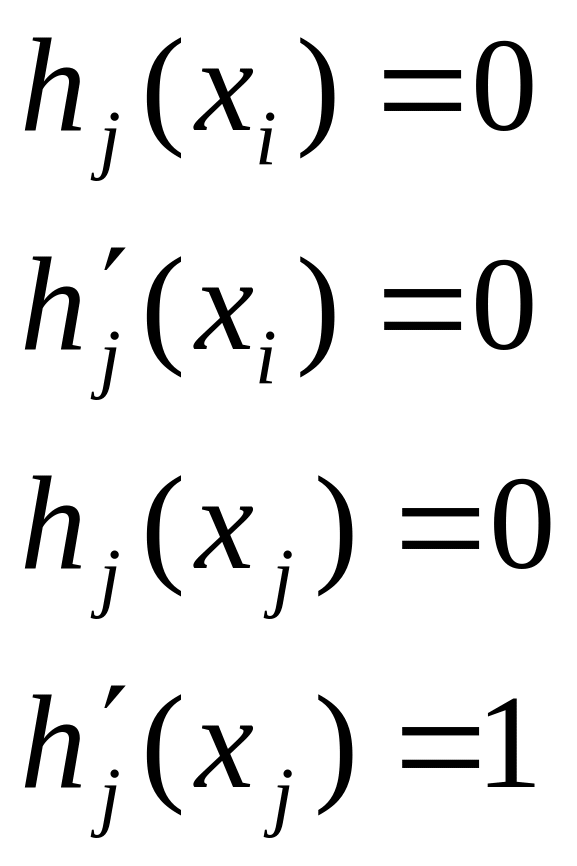
если они найдены, то имеет место

Определим Если и , то должен содержать множитель

Если , а , то должен содержать простой множитель :

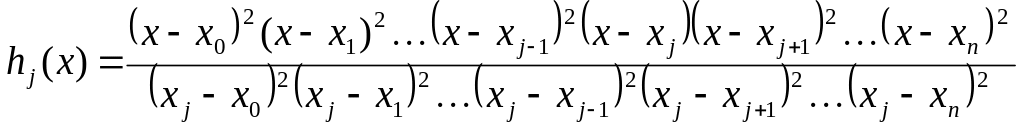
Аналогичным образом можно получить . При будут получены множители чтобы и . Но для того, чтобы и необходим множитель в виде , тогда

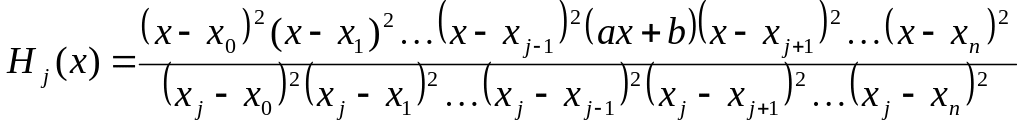(3.1)

Взяв производную от и положив , получим

(1) (3.2)

По условию , т.е. . Из (3.2) , где .

И, наконец, .

Возможно приближение в точках i по производным более высокого порядка. Метод справедлив для произвольного расположения точек. Для равноотстоящих значений аргумента формулы несколько упрощаются. В практических расчётах чаще используется именно этот случай.

3.3.Интерполяционная формула Ньютона.

Удобна тем, что позволяет легко изменять в процессе счета количество используемых узлов. Применима для равномерного и произвольного расположения узлов.

Имеем точек для , через которые проходит многочлен

(3.3)

Формулу Ньютона удобно использовать с помощью таблицы № 3.1 . Знаком * обозначены опорные значения, необходимые для вычисления многочлена.

Таблица № 3.1

		*
				*

Структура разностей группируется относительно опорных значений, которые обозначены значком *. Они введены следующим образом: и . Упрощенно они обозначены Индекс соответствует первой , второй и т.д. разности.

Введём понятие – разделённые разности – это разности функций в некоторых точках отнесённые к разности аргументов в этих точках:

… …

Первые разделённые разности – близки к первым производным в интервале между узловыми точками. Вторые разделённые разности близки ко вторым производным и т.д.

Для равноотстоящих значений аргумента формула Ньютона приобретает следующий вид. Пусть и . Обозначим .

-для интерполяции “вперёд”.

-для интерполяции “назад”.

Получили аналог ряда Тейлора. Для полиномов степени n он конечен.

Покажем близость разделенных разностей к соответствующим производным.

- первая производная.

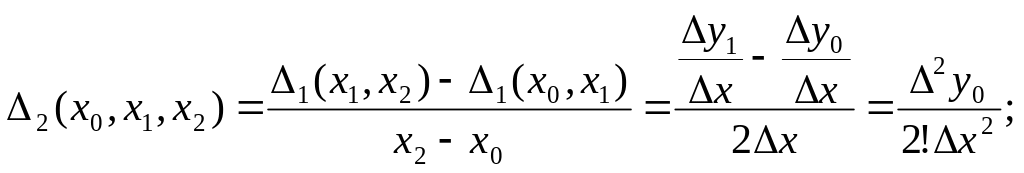- вторая производная.

… …

- производная n-го порядка.

Производные можно определять различным способом.

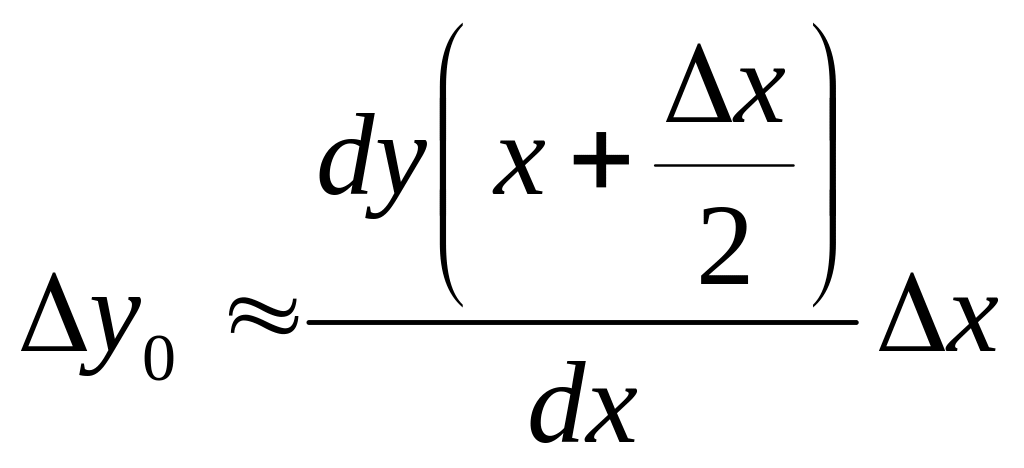Производные определяются в точках между

, узлами.

,

… …

.

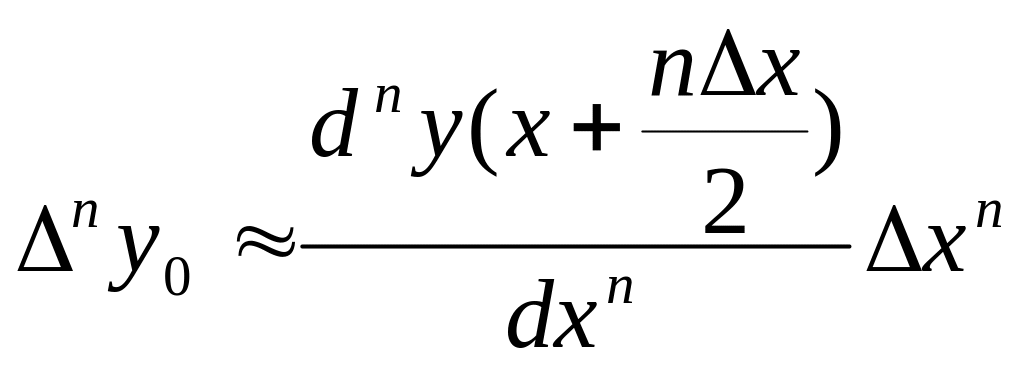При определении производных в граничных точках следует использовать аппроксимацию производных способами “вперёд” или “назад”.

Приведем программу интерполяции методом Ньютона.

function [C,D]=newpoly(X,Y)

%Вектор абсцисс X

%Вектор ординат Y

%Вектор коэффициентов интерполирующего полинома С

%Таблица разностных отношений D

% Обращение из МАTLAB: X=0:0.5:2; Y=exp(-X).*sin(3*X); [C,D]=newpoly(X,Y)

n=length(X);

D=zeros(n,n);

D(:,1)=Y';

%Расчет разностных соотношений

for j=2:n

for k=j:n

D(k,j)=(D(k,j-1)-D(k-1,j-1))/(X(k)-X(k-j+1));

end

end

%Определение коэффициентов интерполирующего полинома С

C=D(n,n);

for k=(n-1):-1:1

C=conv(C,poly(X(k)));

m=length(C);

C(m)=C(m)+D(k,k);

end

X=0:0.1:2;

Y=exp(-X).*sin(3*X); Y1=C(1).*X.^4+C(2).*X.^3+C(3).*X.^2+C(4).*X;

plot(X,Y,X,Y1)