
- •Тема III – основы математического анализа
- •§8. Множества и операции над ними
- •8.1. Основные понятия
- •8.2. Числовые множества
- •9. Функция
- •9.1. Понятия функции и ее графика
- •9.2. Способы задания функций
- •9.3. Некоторые свойства функций
- •9.4. Обратная функция
- •9.5. Основные элементарные функции
- •9.5. Сложная функция и элементарные функции
- •§10. Предел функции
- •10.1. Предел функции в точке
- •10.2. Односторонние пределы
- •10.3. Предел функции на бесконечности
- •10.4. Бесконечно большие функции
- •§11. Бесконечно малые функции
- •11.1. Определение и основные теоремы
- •11.2. Основные теоремы о пределах
- •11.3. Техника вычисления пределов. Примеры
- •11.4. Первый замечательный предел
- •11.5. Эквивалентные функции
- •11.6. Второй замечательный предел
- •11.7. Техника вычисления пределов вида .
- •§12. Непрерывность функции
- •12.1. Непрерывность функции в точке и в области
- •12.2. Основные теоремы о непрерывных функциях
- •12.3. Классификация точек разрыва
- •§13. Производная функции
- •13.1. Приращение аргумента и приращение функции
- •13.2. Определение производной функции в точке
- •13.3. Геометрический смысл производной
- •13.4. Физический смысл производной
- •13.5. Дифференцируемость функций
- •13.6. Производная постоянной, суммы, произведения и частного двух функций
- •13.7. Производная сложной и обратной функции
- •13.8. Производные основных элементарных функций
- •13.9. Производная функции, заданной неявно
- •13.10. Логарифмическая производная
- •13.11. Производная функции, заданной параметрически
- •13.13. Примеры вычисления производных
- •13.14. Производные высших порядков
- •§14. Дифференциал функции
- •14.1. Понятие дифференциала функции
- •14.2. Основные теоремы о дифференциалах
- •14.3. Применение дифференциала к приближенным вычислениям
- •§15. Исследование функций при помощи производных
- •15.1. Правило Лопиталя
- •15.2. Некоторые теоремы о дифференцируемых функциях
- •15.3. Исследование поведения функций и построение графиков
- •Общее исследование функции и построение ее графика рекомендуется выполнять по следующей схеме:
13.7. Производная сложной и обратной функции
Теорема
13.5.
Если
в точке
имеет производную
![]() ,
а
в точке
имеет производную
,
а
в точке
имеет производную
![]() ,
то
,
то
![]() .
.
Теорема
13.6.
Если функция
строго монотонна на интервале (a,b)
и имеет неравную нулю производную
в произвольной точке этого интервала,
то обратная ей функция
также имеет производную
![]() в соответствующей точке, определяемую
равенством
в соответствующей точке, определяемую
равенством
![]() .
.
13.8. Производные основных элементарных функций
Производная показательной функции.
Пусть
![]() .
Тогда
.
Тогда
![]() .
.
![]()
![]()
![]() .
Таким образом,
.
Таким образом,
![]() В
частности,
В
частности,
![]() .
.
Производная логарифмической функции.
Пусть . Тогда
![]() .
.

Таким образом,
![]()
Производная степенной функции.
Пусть
.
Прологарифмируем данное выражение.
Имеем:
![]() ,
откуда
,
откуда
![]() Возьмем производную от сложной функции:
Возьмем производную от сложной функции:
![]() .
.
Таким образом,
![]() .
.
Производные синуса и косинуса.
Пусть
.
Тогда
![]() .
Представим разность тригонометрических
функции в виде произведения:
.
Представим разность тригонометрических
функции в виде произведения:
![]()
Следовательно,
![]()
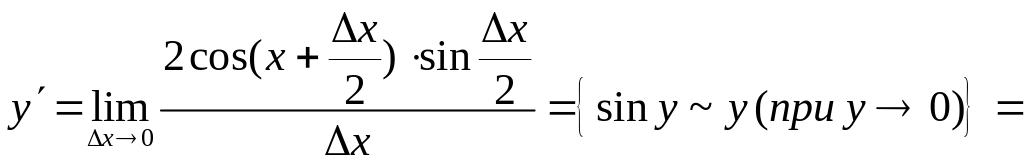

Таким образом,
![]()
Предоставим читателю, доказать формулу:
![]()
Производные тангенса и котангенса.
Пусть
.
Тогда
![]() ,
и на основании правила дифференцирования
дроби, получаем:
,
и на основании правила дифференцирования
дроби, получаем:
![]()
![]()
![]()
![]() .
.
Таким образом,
![]()
Аналогично
для функции
![]() ,
получим
,
получим
![]()
Производные обратных тригонометрических функций
Пусть
.
Тогда
![]() .
По теореме о дифференцировании обратной
функции имеем,
.
По теореме о дифференцировании обратной
функции имеем,
![]() .
.
Пусть
.
Тогда
![]() .
Имеем:
.
Имеем:
 .
.
13.9. Производная функции, заданной неявно
Пусть
![]() неявная функция. Чтобы найти производную
от неявной функции необходимо взять
производную от каждой части равенства
и учесть, что
неявная функция. Чтобы найти производную
от неявной функции необходимо взять
производную от каждой части равенства
и учесть, что
![]() – сложная функция. Так,
– сложная функция. Так,
![]() ;
;
![]() ;
;
![]() и т.д.
и т.д.
Пример.
Найдем производную для функции
![]() .
.
![]()
![]()
![]()
 .
.
13.10. Логарифмическая производная
Пусть
![]() .
Прологарифмируем данную функцию. Тогда
.
Прологарифмируем данную функцию. Тогда
![]() .
Данная функция является неявной. Найдем
ее производную:
.
Данная функция является неявной. Найдем
ее производную:
![]()
![]() .
Тогда
.
Тогда
![]() .
.
Пример.
Найдем производную функции
![]() .
.
Прологарифмируем
функцию:
![]() ,
следовательно,
,
следовательно,
![]() .
.
13.11. Производная функции, заданной параметрически
Пусть
![]() .
Вычислим
.
Вычислим
![]() .
Поскольку
.
Поскольку
![]() ,
т.е.
,
т.е.
![]() Воспользуемся теоремой о производной
сложной функции:
Воспользуемся теоремой о производной
сложной функции:
![]() .
Тогда, по теореме о дифференцировании
обратной функции, имеем:
.
Тогда, по теореме о дифференцировании
обратной функции, имеем:
![]() .
.
Пример.
Найти
производную функции, заданной
параметрически, если
![]() .
.
Имеем:
 .
.
13.12. Сводная таблица формул дифференцирования
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13.13. Примеры вычисления производных
1)
![]() .
.
Для
вычисления производной сначала
преобразуем нашу функцию:
![]() .
.
Тогда
имеем:
![]()
![]()
![]() .
.
2)
![]() .
Здесь воспользуемся формулой производной
произведения. Имеем:
.
Здесь воспользуемся формулой производной
произведения. Имеем:
![]() .
.
3)
![]() .
.
Воспользуемся формулой производной отношения:

![]()
![]() .
.
4)
![]() .
.
Данная функция является сложной, что дает нам право воспользоваться соответствующей формулой. Имеем:
![]() .
.
5)
![]() .
.
![]() .
.
6)
![]() .
.
![]()
![]()
7)
![]() .
.

 .
.
8)
![]() .
.
Данная
функция является неявной. Продифференцируем
обе части равенства:
![]()
![]()
![]()
![]() .
.
9) . Для решения данной задачи прологарифмируем обе части равенства и вычислим производную неявной функции.
![]()
![]()
![]()
![]()
![]() .
.
10)
![]() .
.
Прологарифмируем обе части равенства:
![]()
![]()
![]() .
.
Далее продифференцируем неявную функцию:
![]()
![]()
![]() .
.
