11.5. Эквивалентные функции

• Если , где и БМФ, то называется эквивалентной к при , пишут .

Таким образом, поскольку функции и являются бесконечно малыми при , то они являются эквивалентными при , т.е. .

Теорема 11.11. Предел отношения двух бесконечно малых не изменится, если каждую или одну из них заменить эквивалентной ей БМФ.

Примеры.

1)

2) . В данном случае заменить невозможно, поскольку функция не является бесконечно малой при .

• Вообще говоря, если и БМФ при , то:

1. если , то ;

2. если существует конечный предел , то и - БМФ одного порядка малости;

3. если , то - БМФ более высокого порядка малости, чем ;

4. если , то БМФ более низкого порядка малости, чем .

Говорят, что БМФ одного порядка стремятся к нулю с одинаковой скоростью.

Теорема 11.12 Сумма конечного числа БМФ эквивалентна слагаемому низшего порядка.

Пример: при .

• Слагаемое, эквивалентное сумме бесконечно малых, называется главной частью этой суммы. Замена суммы БМФ ее главной частью называется отбрасыванием БМФ высшего порядка.

Теорема 11.13. Разность двух эквивалентных БМФ есть БМФ более высокого порядка.

Ниже представлены эквивалентные бесконечно малые, используемые при решении задач на вычисление пределов.

Примеры.

1) .

2) .

3) . Для решения данной задачи сделаем замену переменной. Пусть , тогда . Имеем:

= .

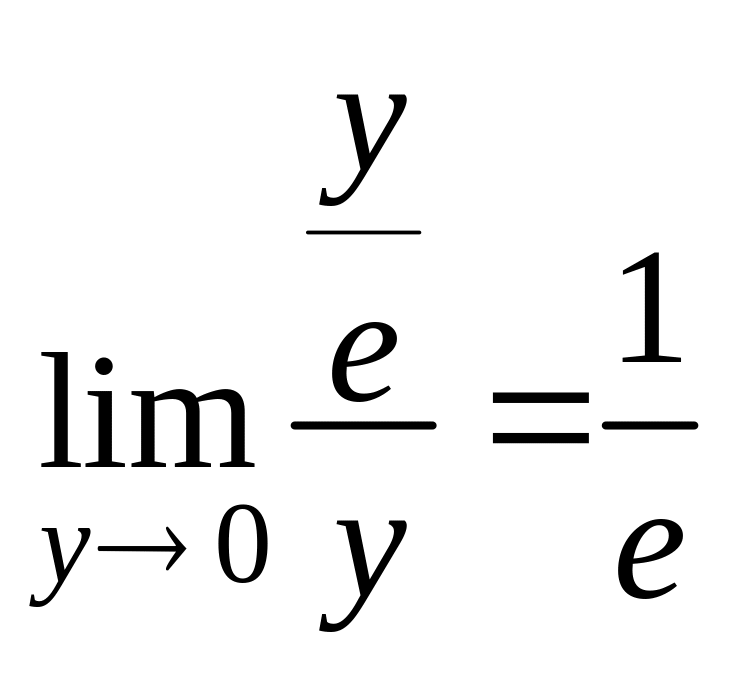11.6. Второй замечательный предел

Вторым замечательным пределом называется предел вида

.

На графике функции , представленном ниже, видно, что при данная кривая стремится к некоторому значению, приблизительно равному 2, 72.

Данное число является иррациональным, оно названо в честь Леонардо Эйлера, Это число известно читателю как основание натурального логарифма.

Итак,

.

Нижеприведенная формула является обобщением второго замечательного предела и используется при вычислениях.

11.7. Техника вычисления пределов вида .

Пусть , , а .

Если и , то .

Пример 1. .

Так как , а , тогда .

Если , а , то

	С=0	С=
	С=	С=0

Пример 2. .

Так как , а , тогда .

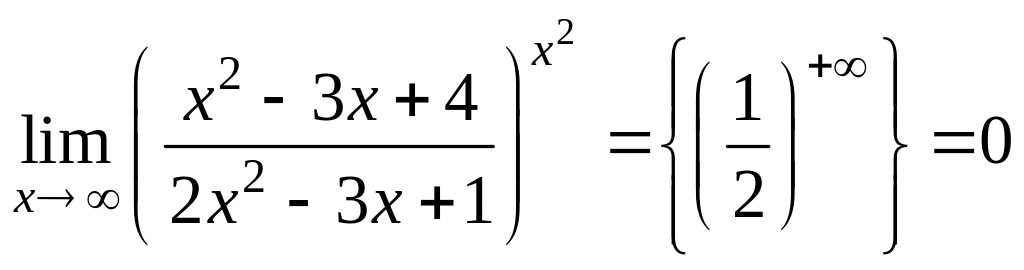В случае А = 1, используем формулу

Пример 3. =

.

§12. Непрерывность функции

12.1. Непрерывность функции в точке и в области

• Пусть определена в точке и в некоторой окрестности этой точки. Функция называется непрерывной в точке , если

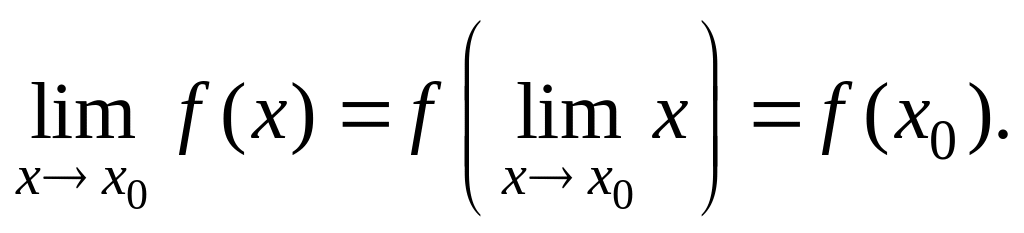
Таким образом, чтобы функция была непрерывна в точке необходимо выполнение следующих 3 условий:

1. функция должна быть определена в точке и в окрестности этой точки;

2. должен существовать предел ;

3. 

На этом рисунке функция непрерывна в точке Ниже представлены примеры функций, имеющих разрыв при .

• Другими словами, функция непрерывна, если предел функции слева равен пределу справа и равен значению функции в данной точке, т.е. .

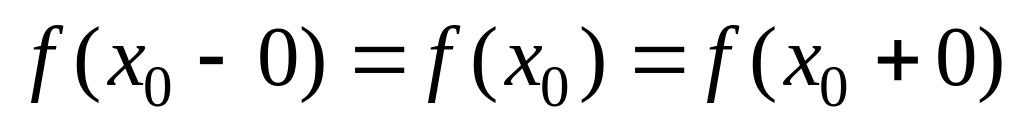• Функция называется непрерывной в интервале (a, b), если она непрерывна в каждой точке этого интервала.

Функция называется непрерывной на отрезке [a, b], если она непрерывна в интервале (a, b) и в точке х=а непрерывна справа, т.е. , а в точке х=b непрерывна слева, т.е.

Утверждение. Все основные элементарные функции непрерывны на своих областях определения.

Это утверждение означает, что при вычислении пределов, используя определение непрерывности, функцию и предел можно поменять местами, т.е.

; ; и т.д.