
- •Тема III – основы математического анализа
- •§8. Множества и операции над ними
- •8.1. Основные понятия
- •8.2. Числовые множества
- •9. Функция
- •9.1. Понятия функции и ее графика
- •9.2. Способы задания функций
- •9.3. Некоторые свойства функций
- •9.4. Обратная функция
- •9.5. Основные элементарные функции
- •9.5. Сложная функция и элементарные функции
- •§10. Предел функции
- •10.1. Предел функции в точке
- •10.2. Односторонние пределы
- •10.3. Предел функции на бесконечности
- •10.4. Бесконечно большие функции
- •§11. Бесконечно малые функции
- •11.1. Определение и основные теоремы
- •11.2. Основные теоремы о пределах
- •11.3. Техника вычисления пределов. Примеры
- •11.4. Первый замечательный предел
- •11.5. Эквивалентные функции
- •11.6. Второй замечательный предел
- •11.7. Техника вычисления пределов вида .
- •§12. Непрерывность функции
- •12.1. Непрерывность функции в точке и в области
- •12.2. Основные теоремы о непрерывных функциях
- •12.3. Классификация точек разрыва
- •§13. Производная функции
- •13.1. Приращение аргумента и приращение функции
- •13.2. Определение производной функции в точке
- •13.3. Геометрический смысл производной
- •13.4. Физический смысл производной
- •13.5. Дифференцируемость функций
- •13.6. Производная постоянной, суммы, произведения и частного двух функций
- •13.7. Производная сложной и обратной функции
- •13.8. Производные основных элементарных функций
- •13.9. Производная функции, заданной неявно
- •13.10. Логарифмическая производная
- •13.11. Производная функции, заданной параметрически
- •13.13. Примеры вычисления производных
- •13.14. Производные высших порядков
- •§14. Дифференциал функции
- •14.1. Понятие дифференциала функции
- •14.2. Основные теоремы о дифференциалах
- •14.3. Применение дифференциала к приближенным вычислениям
- •§15. Исследование функций при помощи производных
- •15.1. Правило Лопиталя
- •15.2. Некоторые теоремы о дифференцируемых функциях
- •15.3. Исследование поведения функций и построение графиков
- •Общее исследование функции и построение ее графика рекомендуется выполнять по следующей схеме:
Общее исследование функции и построение ее графика рекомендуется выполнять по следующей схеме:
Найти область определения функции.
В случае если область определения функции симметрична относительно начала координат, проверить, не является ли функция четной или нечетной, проверить периодичность функции.
Найти, если это возможно, точки пересечения графика функции с осями координат.
Найти промежутки знакопостоянства функции (промежутки на которых
 или
или
 );
выяснить поведение функции на концах
промежутка знакопостоянства (в том
числе и на бесконечности), построить
схематично график на концах промежутка
знакопостоянства.
);
выяснить поведение функции на концах
промежутка знакопостоянства (в том
числе и на бесконечности), построить
схематично график на концах промежутка
знакопостоянства.Найти асимптоты графика функции.
Найти промежутки монотонности функции, ее экстремумы.
Найти промежутки выпуклости и вогнутости графика функции, его точки перегиба.
Построить график, используя полученные результаты исследования.
Заметим, что приведенная схема исследования не является обязательной. Иногда целесообразно выполнение операций сопровождать постепенным построением графика функции и выбирать дополнительные точки.
Пример.
Исследовать
функцию
![]() .
.
1.
Данная функция определена при всех
,
т.е.
![]() .
.
2.
![]()
данная функция является функцией общего
вида.
данная функция является функцией общего
вида.
3.
Если
![]() .Таким
образом график функции пересекает ось
.Таким
образом график функции пересекает ось
![]() в точке
в точке
![]() .
Если
.
Если
![]() .
График пересекает ось
в точках
.
График пересекает ось
в точках
![]() и
и
![]() .
.
4. Интервалы знакопостоянства:
|
|
0 |
|
|
|
|
– |
0 |
– |
0 |
+ |
5. Вертикальных асимптот нет, поскольку функция непрерывна на всей области определения. Выясним наличие наклонной асимптоты :
![]() ,
,
![]() .
Таким образом, наклонных асимптот нет.
.
Таким образом, наклонных асимптот нет.
6. Найдем промежутки монотонности функции.
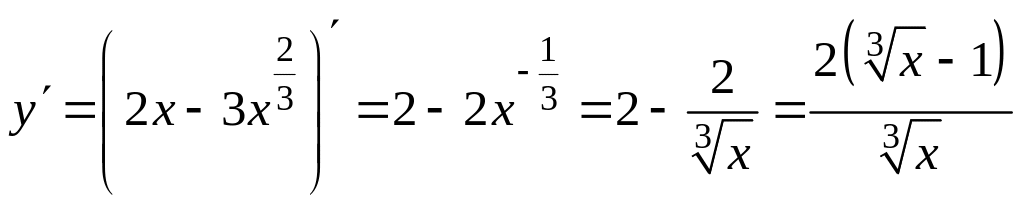 .
.
|
х |
|
0 |
(0;1) |
1 |
|
|
+ |
|
– |
0 |
+ |
|
у |
|
0 |
|
-1 |
|
Таким
образом
![]() ,
,
![]() .
.
7.
Найдем промежутки выпуклости и вогнутости
графика функции.
 .
Вторая производная положительна (кривая
вогнута) при всех
,
кроме
.
.
Вторая производная положительна (кривая
вогнута) при всех
,
кроме
.
|
|
0 |
|
|
+ |
|
+ |
|
|
0 |
|
8.


