
- •Задачи а
- •6. Найти общее решение дифференциального уравнения .
- •16. Является ли функция решением уравнения ?
- •10.2. Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли
- •5. Решить задачу Коши: .
- •10.3. Дифференциальные уравнения второго порядка, допускающие понижение порядка
- •Задачи а
- •5. Решить задачу Коши:
- •18. Решить задачу Коши: .
- •10.4. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами со специальной правой частью
- •2. Решить задачу Коши .
- •14. Решить задачу Коши .
- •19. Решить задачу Коши .
- •10.5. Численные методы решения дифференциальных уравнений: метод Эйлера, метод Рунге – Кутты
- •Задания для выполнения лабораторной работы
- •Решение типовых задач
- •Контрольные задания по теме «Дифференциальные уравнения»
- •4. Найти общее решение дифференциального уравнения .
- •6. Найти общее решение дифференциального уравнения
- •12. Найти общее решение дифференциального уравнения .
10. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
10.1. Дифференциальные уравнения первого порядка.
Дифференциальные уравнения
с разделяющимися переменными, однородные
Основные понятия: дифференциальное уравнение первого порядка, решение, общее решение, общий интеграл, задача Коши, частное решение, интегральная кривая, теорема существования и единственности решения задачи Коши; дифференциальное уравнение с разделяющимися переменными, однородное уравнение первого порядка [1, с. 417-421].
Дифференциальным
уравнением первого порядка относительно
искомой функции
![]() называется уравнение вида
называется уравнение вида
![]() .
.
Дифференциальное уравнение первого порядка, разрешенное относительно производной, имеет вид
![]() .
.
Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если его можно представить в виде
![]() или
или
![]() .
.
При решении таких уравнений сначала разделяют переменные , потом находят общий интеграл, при этом возможна потеря решений (см. решение типовых задач, пример 3).
Однородное дифференциальное уравнение 1-го порядка имеет вид
 (10.1)
(10.1)
или
![]() ,
,
где
![]() и
и
![]() однородные функции степени
однородные функции степени
![]() ,
т.е.
,
т.е.
![]() и
и
![]()
![]() .
.
Однородное
уравнение (10.1) с помощью подстановки
![]() (
(![]()
![]() ),
где
),
где
![]() новая
неизвестная функция, приводится к
дифференциальному уравнению с
разделяющимися переменными.
новая
неизвестная функция, приводится к
дифференциальному уравнению с
разделяющимися переменными.
Задачи а
1. Является
ли функция
![]() решением уравнения
решением уравнения
![]() ?
?
2. Найти
общее решение дифференциального
уравнения
![]() .
.
3. Решить
задачу Коши
![]() .
.
4. Проверить,
что функции
![]() и
и
![]() являются решениями уравнения
являются решениями уравнения
![]() проходящими через точку (0; 0). Какое
условие теоремы существования и
единственности решения здесь нарушается?
проходящими через точку (0; 0). Какое
условие теоремы существования и
единственности решения здесь нарушается?
5. Какие
из дифференциальных уравнений являются
уравнениями с разделяющимися переменными:
а) ![]() ;
;
б)
![]() ; в)
; в) ![]() ?
?
6. Найти общее решение дифференциального уравнения .
7. Установить соответствие между дифференциальными уравнениями:
1)
![]() 2)
2)
![]() 3)
3)
![]()
и общими решениями:
А)
![]() В)
В)
![]() С)
С)
![]() D)
D)
![]()
8. Какие из дифференциальных уравнений являются однородными уравнениями:
а)![]() ;
б)
;
б)![]() ;
в)
;
в)
![]() ?
?
Задачи Б
Решить дифференциальные уравнения:
9.
![]() . 10.
. 10.
![]() . 11.
. 11. ![]() ;
;
Решить задачу Коши:
12.
![]() . 13.
. 13.
![]() .
.
14.
![]()
![]() .
.
15.
Построить интегральную кривую уравнения
![]() ,
проходящую через точку
,
проходящую через точку
![]() .
.
Домашнее задание
16. Является ли функция решением уравнения ?
Решить дифференциальные уравнения:
17.
![]() .
18.
.
18.
![]() .
19.
.
19.
![]() .
.
Решить задачу Коши:
20.
![]() ,
,
![]() .
21.
.
21.
![]() .
.
Дополнительные задачи
22. Решить
дифференциальное уравнение
![]() .
.
Решить задачу Коши:
23.
![]() .
24.
.
24.
![]() .
.
25.
 .
26.
.
26.
![]() .
.
Решение типовых задач
Пример 1.
Проверить, являются ли функции
![]() ,
,
![]() решениями дифференциального уравнения
решениями дифференциального уравнения
![]() .
.
![]() Функция
будет решением, т.к.
Функция
будет решением, т.к.
![]() и
и
![]() для всех
для всех
![]() А функция
не является решением дифференциального
уравнения ни на каком интервале, т.к.
А функция
не является решением дифференциального
уравнения ни на каком интервале, т.к.
![]() и равенство
и равенство
![]() выполняется только для отдельных
значений
выполняется только для отдельных
значений
![]() – нет такого интервала, на котором
равенство выполнялось бы для всех
.
– нет такого интервала, на котором
равенство выполнялось бы для всех
.
![]()
Пример 2.
Решить задачу Коши
![]() .
.
![]() Исходное уравнение можно записать в
виде
Исходное уравнение можно записать в
виде
![]() .
.
Разделяя переменные, будем
иметь
 .
Интегрируя по
обе части этого уравнения
.
Интегрируя по
обе части этого уравнения
 ,
,
 ,
,
получим общий интеграл
![]() ,
,
![]() .
.
Потенцируя последнее
равенство, получим
![]()
или
 ,
где
,
где
![]() ,
,
![]() .
.
Решением уравнения также
будет:
![]() .
Таким образом, общее решение
дифференциального уравнения имеет вид
,
.
Таким образом, общее решение
дифференциального уравнения имеет вид
,
![]() .
.
Далее, используя заданное
начальное условие
![]() ,
получим
,
получим
 ,
откуда
,
откуда
![]() .
Следовательно, искомое частное решение
имеет вид
.
Следовательно, искомое частное решение
имеет вид
![]() .
.
![]()
Пример 3.
Решить уравнение
![]() .
.
Разделяя переменные и интегрируя
 ,
получим
,
получим
![]() ,
или
,
или
![]() ,
где
,
.
,
где
,
.
При делении на
![]() и
и
![]() потеряли решения
потеряли решения
![]() ,
,
![]() .
Итак, общее решение уравнения имеют
вид:
.
Итак, общее решение уравнения имеют
вид:
![]() .
Решениями также являются
.
Решениями также являются
![]() .
.
Пример
4.
Решить дифференциальное уравнение
![]() .
.
Разделив обе части уравнения на
![]() ,
получим
,
получим
 .
.
Это однородное дифференциальное
уравнение. Полагаем
![]() ,
тогда
и уравнение принимает вид
,
тогда
и уравнение принимает вид
![]() или
или
![]() .
Это уравнение с разделяющимися
переменными:
.
Это уравнение с разделяющимися
переменными:
 ,
,
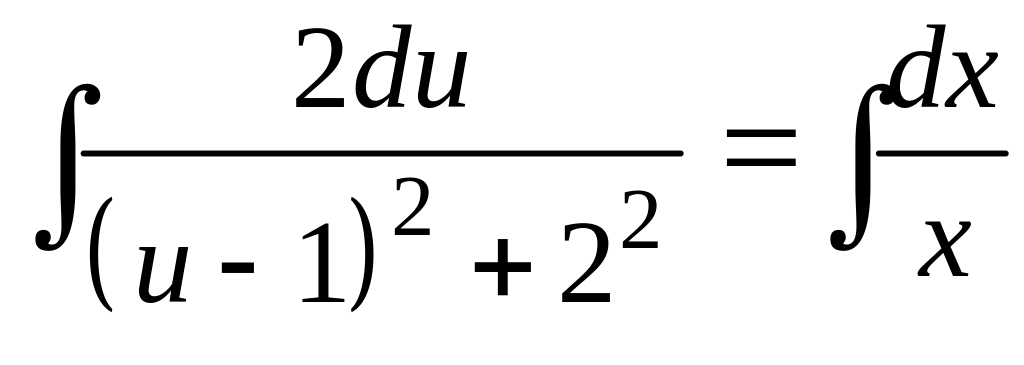 ,
,
![]() .
.
Так как
![]() ,
то общий интеграл уравнения:
,
то общий интеграл уравнения:
![]() .
.
Ответы
9.
![]() 10.
10. ![]() .
11.
.
11.
![]() .
.
12.
![]() .
13.
.
13. ![]() .
14.
.
14.
![]() .
15.
.
15. ![]() .
16. Да.
.
16. Да.
17.
 .
18.
.
18. ![]() ,
,
![]() .
19.
.
19. ![]() 20.
20.  .
21.
.
21.
 .
22.
.
22.  ,
,
![]() .
23.
.
23. ![]() .
24.
.
24. ![]() .
25.
.
25. 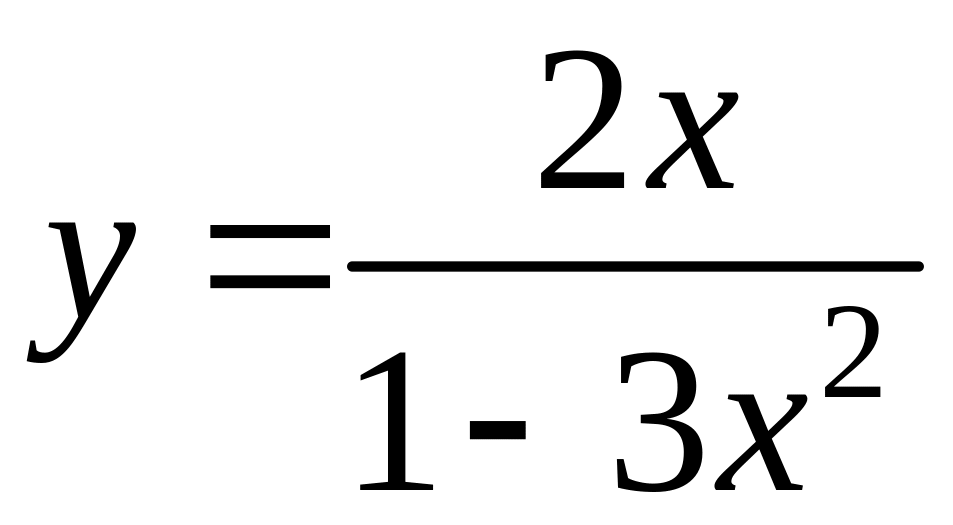 .
26.
.
26.
![]() .
.
10.2. Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли
Основные понятия: линейное дифференциальное уравнение первого порядка, уравнение Бернулли [1, с. 422-423].
Линейное дифференциальное уравнение первого порядка имеет вид
![]() .
.
По
методу Бернулли (см. комментарий с. 226)
решение этого уравнения ищут в виде:
![]() .
(см. решение типовых задач, пример 1).
.
(см. решение типовых задач, пример 1).
Линейное
дифференциальное уравнение первого
порядка относительно функции
![]() :
:
![]() .
.
Уравнение Бернулли имеет вид:
![]() .
.
Решение
уравнения Бернулли можно также искать
в виде
![]() .
.
Задачи А
1. Определить типы уравнений и указать способы их решения:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ; е)
; е)
 ;
;
ж)
![]() ; з)
; з)
![]() .
.
Задачи Б
Решить дифференциальные уравнения:
2.
 .
3.
.
3.
![]() .
4.
.
4.
![]() .
.
