2 Обоснование методики эксперимента

Из формулы (14) следует, что для определения ускорения свободного падения необходимо знать период колебаний математического маятника Т и его длину l, определение которой в лабораторных условиях не всегда возможно. Поэтому в экспериментальной установке используют нить (трос) с изменяющейся длиной. В качестве материальной точки применяют тело, формой и размерами которого в рассматриваемых условиях можно пренебречь (его диаметр много меньше длины подвеса). Определяем период колебаний математического маятника Т₁ при длине l₁, а затем изменяем длину нити и определяем новый период колебаний маятника Т₂ при длине l₂. Получим

, (17)

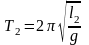. (18)

Возведем Т2 и Т1 в квадрат и вычтем Т1 из Т2 .Получим

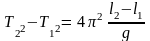, (19)

_откуда

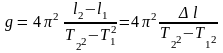. (20)

_{Применим эту формулу в лабораторной работе. Из нее следует, что для опытного определения ускорения свободного падения достаточно экспериментально найти изменение длины маятника ∆l и периоды колебаний Т1 и Т2.}

3 Описание установки и порядок выполнения работы

_{1. Лабораторная установка состоит из стальной проволоки, длину которой можно менять, и подвешенного на ней чугунного шара. Проволока вверху переброшена через блок и вторым концом прикреплена к указателю, который может, если отвинтить винт, передвигаться вдоль шкалы h с сантиметровыми делениями. Чтобы изменять длину l маятника, следует перемещать его вдоль шкалы. Для этого поступают следующим образом: один студент двумя руками поддерживает шар и слегка приподнимает его, а второй отвинчивает винт на указателе и перемещает его вдоль шкалы. И только, когда он закрепит винт в нужном положении, первый студент постепенно отпускает шар.}

_{2. Зафиксировав указатель в положении h1 ближе к нижнему пределу шкалы, запишите его. При этом длина маятника примет значение равное l1.}

_{3. Отклоните маятник на 3о-5о и отпустите его. При малых колебаниях угловое отклонение математического маятника изменяется со временем по гармоническому закону. Пропустив 3-4 полных колебания, включите секундомер, и определите время t1 '} двадцати полных колебаний (n=20). Затем повторите эту операцию дважды, определите t1", t1" и найдите t1 ср

_{. (21)}

Определите период колебаний Т1

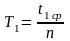_{. (22)}

4. Обращаясь с маятником так, как описано в пункте 1, измените длину маятника не менее чем на 60см. Зафиксируйте указатель винтом и запишите значение шкалы h2, на уровне которого он находится. При этом длина маятника примет соответствующее значение l2.

5. Повторите действия пункта 3. Определите соответственно t2 ср и период колебаний маятника Т2.

6. По формуле (20) рассчитайте ускорение свободного падения g_1, учитывая, что ∆l=h₂-h₁ соответствует изменению длины маятника.

7. Повторите действия пунктов 1-5 еще для двух разных длин маятника и рассчитайте g₂ и g₃. Определите среднее значение g.

8. Сравните полученное значение g с табличным значением (g₀=9,81м/с²) и рассчитайте относительную погрешность по формуле:

₍₂₃₎