
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение высшего профессионального образования
«Национальный исследовательский ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Наименование института – Институт Кибернетики
Наименование направления – Стандартизация и метрология
Наименование кафедры – Компьютерных измерительных систем и
метрологии
ОПРЕДЕЛЕНИЕ ТОЧЕЧНЫХ И ИНТЕРВАЛЬНЫХ ОЦЕНОК ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
Отчет о лабораторной работе №3
по курсу «Статистические методы контроля и управления качеством»
Вариант 8
Студентка гр. 1г90 е. В. Шишкова Преподаватель в.Ю.Казаков Томск 2011
1. Цель работы: изучение правил определения и методов расчета статистических характеристик по выборочным данным; получение точечных и интервальных оценок среднего, медианы, дисперсии, среднеквадратичного отклонения.
2. Используемые технические средства: компьютерный класс, специализированный программный пакет статистических вычислений.
3. Программа работы.
Ознакомиться с краткой сводкой теоретических положений (см. Приложение 1.) и рекомендованной литературой.
Используя генератор случайных чисел, получить выборочные данные для своего варианта и выполнить задание.
Сделать выводы и оформить отчет о проделанной лабораторной работе.
Задание.
Используя генератор случайных чисел, получить данные для своего варианта. Для получения точечной и интервальной оценок мат. ожидания заполнить таблицу 6.2 из [6]. Для получения точечной и интервальной оценок дисперсии заполнить таблицу 7.1 из [6]. Использовать статистические таблицы. Исходя из [5] получить точечные и интервальные оценки для медианы распределения генеральной совокупности. По образцу заполнить таблицы В.1 и В.2 из [5].
4. Ход работы:
1) Используя генератор случайных чисел, получаем данные Варианта №8.
2) Заполняем таблицу 6.2, получаем точечную и интервальную оценку мат. ожидания.
Таблица 6.2 - Оценка среднего значения при неизвестной дисперсии
Статистические и исходные данные
|
Табличные данные и вычисления
|
1 Объем выборки:
|
1 Квантиль распределения
Стьюдента уровня (
|
2 Сумма значений наблюдаемых величин:
|
2 Квантиль распределения
Стьюдента уровня (
|
3 Сумма квадратов значений наблюдаемых величин:
|
3 Вычисляем:
|
4 Степени свободы:
=30-1=29 |
4 Вычисляем:
|
5 Выбранная доверительная вероятность:
=1-0,01=0,99
|
5 Вычисляем:
|
|
6 Вычисляем:
|
|
7 Вычисляем:
|
Результаты:
1 Точечная оценка параметра
|
|
2 Точечная оценка параметра
|
|
3 Двусторонний симметричный доверительный интервал для параметра :
|
|
4 Односторонние доверительные интервалы для параметра :
|
|
Примечание - Квантили распределения Стьюдента определяют по таблице Б.1 приложения Б
|
|
3) Для получения точечной и интервальной оценок дисперсии заполняем таблицу 7.1 . Используем статистические таблицы для определения величины квантили.
Таблица 7.1 - Точечная и интервальная оценки дисперсии или стандартного отклонения
Статистические и исходные данные
|
Табличные данные и вычисления |
1 Объем выборки:
30
|
1 Квантили
|
2 Сумма значений наблюдаемых величин:
13490,12
|
|
3 Сумма квадратов значений наблюдаемых величин:
6067485 |
|
4 Степени свободы:
|
2 Вычисляем:
|
5 Выбранная доверительная вероятность:
=1-0,01=0,99 |
3 Вычисляем:
|
Результаты:
|
|
1 Точечные оценки дисперсии и стандартного отклонения генеральной совокупности:
|
|
2 Двусторонний доверительный интервал* для дисперсии :
|
|
3 Односторонний доверительный интервал* для дисперсии :
_____________
* Значения границ
доверительного интервала стандартного
отклонения
|
|
Примечание - Квантили -распределения определяют по по таблице В.1 приложения В
|
|
Заполняем таблицы В.1 и В.2. Получаем точечные и интервальные оценки для медианы распределения генеральной совокупности.
Таблица В.1 - Вычисление точечной оценки медианы (пример 1)
Бланк для расчета
|
Пример заполнения бланка для расчета
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Предварительная операция
|
Предварительная операция
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Расположите наблюдаемые значения в порядке неубывания, т.е:
|
Расположите наблюдаемые значения в порядке неубывания, т.е:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Исходные данные
|
Исходные данные
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Объем выборки
|
Объем выборки : =30
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а) Объем выборки нечетный
|
а) Объем выборки нечетный
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b) Объем выборки четный
|
b) Объем выборки четный
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Необходимые предварительные вычисления
|
Необходимые предварительные вычисления
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В случае а)
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В случае b)
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
15
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вычисление выборочной
медианы
|
Вычисление выборочной медианы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В случае а)
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
равна
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В случае b)
|
В случае b)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
равна среднеарифметическому
-й
и (
|
равна среднеарифметическому -й и ( )-й порядковых статистик, т.е:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
449,552
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
450,625
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Результат
|
Результат
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Выборочная медиана (точечная оценка медианы совокупности) равна
|
Выборочная медиана (точечная оценка медианы совокупности) равна 450,089
|
Таблица В.2 - Вычисление интервальной оценки медианы (пример 2)
Бланк для расчета
|
Пример заполнения бланка для расчета
|
Предварительная операция
|
Предварительная операция
|
Расположите наблюдаемые значения в порядке неубывания, т.е:
|
Расположите наблюдаемые значения в порядке неубывания, т.е:
|
|
(есть в таблице В1)
|
Исходные данные
|
Исходные данные
|
Объем выборки : =
|
Объем выборки : =30
|
Уровень доверия
|
Уровень доверия : =99%
|
a)
|
a) 100 - односторонний интервал
|
b) 100 - двусторонний интервал
|
b) 100 - двусторонний интервал
|
с) >100 - односторонний интервал
|
с) >100 - односторонний интервал
|
d) >100 - двусторонний интервал
|
d) >100 - двусторонний интервал
|
Для а) и с) в случае верхней
доверительной границы нижняя граница
значений случайной величины в
генеральной совокупности равна:
|
|
Для а) или с) в случае
нижней доверительной границы верхняя
граница значений случайной величины
в генеральной совокупности равна:
|
|
Определение
|
|
В случае а) значение определяется из таблицы 1: =
|
|
В случае b) значение определяется из таблицы 2: =
|
В случае b) значение определяется из таблицы 2: = 8
|
В случае с) значения
|
|
В случае d) значения и определяются из таблицы 4: = =
|
|
В случаях с) или d) значение
|
|
Значение определяется как целая часть значения : =
|
|
Определение доверительных
границ
|
Определение доверительных границ и/или
|
В случаях а) или с) с нижней
доверительной границей, а также в
случаях b) и d):
|
В случаях а) или с) с нижней доверительной границей, а также в случаях b) и d): : =444,369
|
В случаях а) или с) с верхней доверительной границей и в случаях b) и d) необходимо подсчитать
|
В случаях а) или с) с верхней доверительной границей и в случаях b) и d) необходимо подсчитать : =30-8+1=23
|
|
: =453,553
|
Результаты
|
Результаты
|
Односторонний доверительный интервал с нижней доверительной границей для медианы совокупности, соответствующий уровню доверия = %, имеет вид:
|
Односторонний доверительный интервал с нижней доверительной границей для медианы совокупности, соответствующий уровню доверия = 99 %, имеет вид:
|
|
[
|
Односторонний доверительный интервал с верхней доверительной границей для медианы совокупности, соответствующий уровню доверия = %, имеет вид:
|
Односторонний доверительный интервал с верхней доверительной границей для медианы совокупности, соответствующий уровню доверия = 99 %, имеет вид:
|
|
.
|
Двусторонний симметричный доверительный интервал для медианы совокупности, соответствующий уровню доверия = %, имеет вид:
|
Двусторонний симметричный доверительный интервал для медианы совокупности, соответствующий уровню доверия =99%, имеет вид:
|
|
.
|

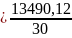 =449,67
=449,67



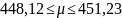
 (1)
(1) 2)
2)
 .
.
 =0,96
(3)
=0,96
(3)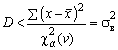 =3,32 (4)
=3,32 (4)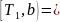 444,369
444,369

