Модуль 4 Теорія ймовірностей і елементи математичної статистики

4.1 Випадкові події. Класична та статистична ймовірності. Основні формули та теореми теорії ймовірностей

Класичне означення ймовірності: Ймовірністю події називають відношення числа сприятних цій події наслідків до загального числа всіх рівноможливих, несумісних елементарних наслідків , що утворюють повну групу, тобто

. (4.1.1)

Основні властивості ймовірності:

1. Ймовірність достовірної події дорівнює одиниці (тому що ).

2. Ймовірність неможливої події дорівнює нулю (тому що ).

3. Ймовірність випадкової події є число, розташоване між нулем і одиницею, тобто .

Переставленнями називають комбінації, складені з тих самих різних елементів, що відрізняються тільки порядком їхнього розташування. Число всіх різних переставлень елементів дорівнює

, (4.1.2)

де . Так, , , , , і т.п.

Розміщеннями називають комбінації, складені з різних елементів по елементів, які відрізняються або складом елементів, або їхнім порядком. Число розміщень знаходять за формулою:

. (4.1.3)

Сполученнями називають комбінації, складені з різних елементів по елементів, які відрізняються хоча б одним елементом. Число сполучень знаходять за формулою:

. (4.1.4)

Правило суми. Якщо деяка подія може відбутися в елементарних наслідках, а інша подія – в наслідках, то подія (або , або , коли події і несумісні) може відбутися в елементарних наслідках.

Правило добутку. Якщо деяка подія може відбутися в елементарних наслідках і після цього інша подія може відбутися в наслідках, то подія (і , і в зазначеному порядку) може відбутися в елементарних наслідках.

○ Приклад 4.1.1. Задумано двозначне число, що не містить нуль. Яка ймовірність відгадати це число з однієї спроби, якщо відомо, що його цифри різні?

Розв'язання. Всього дев'ять цифр, що не містять нуль, тому загальне число можливих елементарних наслідків експерименту дорівнює числу комбінацій вибору двох різних цифр із дев'яти, тобто . Дійсно, першу цифру можна вибрати 9–ма способами, другу (відмінну від першої) вибирають 8–ма способами.

, тому ймовірність події – «відгадано задумане число»:

. ●

○ Приклад 4.1.2. У групі 15 студентів, 10 з яких юнаки. Знайти ймовірність того, що серед узятих навмання 8 студентів: а) виявляться три дівчини; б) не більше трьох дівчин.

Розв'язання. а) Загальне число можливих елементарних наслідків експерименту дорівнює числу способів, якими можна вибрати 8 студентів з 15, тобто .

Визначимо число наслідків , сприятних події – «серед восьми обраних студентів 3 дівчини». Представимо подію у вигляді добутку подій: , де – «обрано 5 юнаків» і – «обрано 3 дівчини». Тоді за правилом добутку , де – число способів вибору юнаків серед юнаків групи та – число способів вибору дівчин серед дівчин групи.

Отже, число наслідків, сприятливих події , . Тоді ймовірність події

.

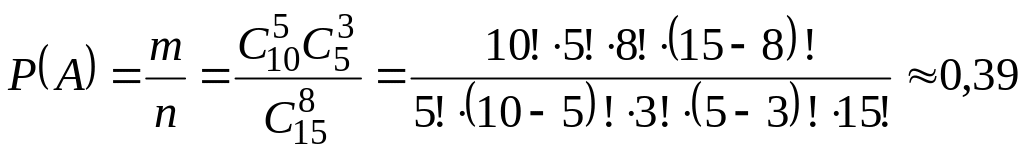б) У цьому випадку подія – «з 8–ми відібраних студентів не більше 3 дівчин» може відбутися по одному із чотирьох варіантів, коли серед 8–ми відібраних студентів немає дівчин (подія ), одна дівчина (подія ), дві дівчини (подія ) і три дівчини (подія ).

Таким чином, подію можна представити у вигляді суми попарно несумісних подій: , тобто відбудеться або подія , або , або , або .

За правилом добутку число наслідків , , і , сприятливих подіям , , і , можна знайти, як і у випадку а): ; ; ; . Загальне число наслідків , сприятливих події , визначимо за правилом суми: .

, тоді ймовірність події

. ●

Основні теореми теорії ймовірностей випадкових подій:

1. Ймовірність настання одного з скінченого числа попарно несумісних подій (або ймовірність суми несумісних подій) дорівнює сумі ймовірностей цих подій, тобто

. (4.1.5)

2. Сума ймовірностей подій , що утворюють повну групу несумісних подій, дорівнює одиниці, тобто

. (4.1.6)

3. Сума ймовірностей протилежних подій дорівнює одиниці, тобто .

4. Ймовірність спільного настання двох залежних подій і (або ймовірність їхнього добутку) дорівнює добутку ймовірності одного з них на умовну ймовірність іншої, обчислену в припущенні, що перше вже наступило, тобто

. (4.1.7)

5. Ймовірність добутку декількох незалежних подій дорівнює добутку ймовірностей цих подій

. (4.1.8)

6. Ймовірність появи хоча б одного з двох сумісних подій і (ймовірність суми сумісних подій) дорівнює сумі ймовірностей цих подій без ймовірності їхньої спільної появи, тобто

. (4.1.9)

○ Приклад 4.1.3. При прийманні товару на склад піддають перевірці 1/4 випадково відібраних виробів. Умова приймання – наявність браку не більше 3%. Обчислити ймовірність того, що партія з 100 виробів, що містить 6% браку, не буде прийнята.

Розв'язання. Тому що припустимо не більше 3 бракованих виробів для партії з 100 виробів (3%), то партія не буде прийнята, якщо з 25 виробів виявиться 4 або 5, або 6 бракованих виробів.

Позначимо події: – «відібрано в групу для перевірки більше трьох бракованих виробів (партія виробів не буде прийнята)»; – «відібране в групу для перевірки чотири бракованих вироби»; – «відібрано п'ять бракованих виробів»; – «відібрано шість бракованих виробів». Тому що , а події несумісні, то ймовірність .

Знайдемо імовірність події . Число наслідків, сприятливих тому, що буде відібрано 21 вироб без браку, , а число наслідків, сприятливих тому, що буде відібрано 4 бракованих вироба, .

За правилом добутку: . Загальне число наслідків .

Знайдемо .

Аналогічно й .

Тоді ймовірність події : . ●

○ Приклад 4.1.4. На окремих картках написані букви Б, К, К, О, О, О, Л. Студент навмання бере по одній картці, та одну за одною викладає їх перед собою. Яка ймовірність того, що вийде слово «КОЛОБОК».

Розв'язання. Подію – «складено слово «КОЛОБОК» запишемо у вигляді добутку , де позначено події: – «першою витягнута карта з буквою К »; – «другою витягнута карта з буквою О»; ...; – «сьомою витягнута карта з буквою К ». Ці події залежні, тому:

; ; ; ...; ; ; ; .

Шукана ймовірність

. ●

○ Приклад 4.1.5. Студент здає в сесію три іспити. Імовірність того, що він здасть на додатну оцінку перший іспит – 0,8, другий – 0,7, а третій – 0,6. Знайти ймовірності подій того, що студент: а) успішно здасть сесію; б) здасть тільки один із трьох іспитів; в) не здасть жодного іспиту; г) здасть хоча б один із цих іспитів?

Розв'язання. Позначимо події: – «студент здасть перший іспит» ( ); – «студент здасть другий іспит» ( ); – «студент здасть третій іспит» ( ); – «студент не здасть перший іспит» ( ); – «студент не здасть другий іспит» ( ); – «студент не здасть третій іспит» ( ). Можна вважати, що події , і , а також протилежні події , , – незалежні.

а) Розглянемо подію – «студент здасть всі три іспити». Ймовірність цієї події

.

б) Подія – «студент здасть тільки один із трьох іспитів» можна представити у вигляді: , де кожне з доданків є несумісною подією. Тоді ймовірність

.

в) Розглянемо подію – «студент не здасть жодного з іспитів». Тоді ймовірність

.

г) Події «студент здасть хоча б один із цих іспитів» і «студент не здасть жодного з іспитів» є протилежними, тому

. ●

○ Приклад 4.1.6. На підприємстві працюють дві бригади. Ймовірність того, що перша з них виконає денний план, дорівнює 0,8, а друга – 0,9. Знайти ймовірність виконання плану хоча б однієї з бригад.

Розв'язання. Розглянемо події: – «план виконаний першою бригадою»; – «план виконаний другою бригадою»; – «план виконаний хоча б однієї з бригад». За умовою задачі й . Події й сумісні і незалежні, тому

. ●

Формула повної ймовірності. Ймовірність події , що може наступити лише за умови появи однієї з несумісних подій , що утворюють повну групу, дорівнює сумі добутків ймовірностей кожної з цих подій на відповідну умовну ймовірність події , тобто

. (4.1.10)

Формула Байеса. Ймовірність події (гіпотези) , обчисленої після того, як подія відбулася, дорівнює

, (4.1.11)

де , тобто ймовірність визначається за формулою повної ймовірності (4.1.10).

○ Приклад 4.1.7. У банк щодня надходять запити на надання кредиту. З них 24% запитів – від приватних підприємств, 46% – від фізичних осіб, а інші – від громадських організацій. Ймовірності неповернення кредиту відповідно дорівнюють 0,05, 0,1 і 0,3. Потрібно знайти ймовірність того, що отримане банком повідомлення про неповернення кредиту за результатами роботи одного дня буде отримано від приватного підприємства.

Розв'язання. Позначимо події: – «запит на кредит надійшов від приватного підприємства»; – «від фізичної особи»; – «від громадської організації». За умовою задачі , і . , і – єдино можливі несумісні події, що утворюють повну групу: .

Розглянемо подію – «отримано банком повідомлення про неповернення кредиту за результатами роботи одного дня». Ця подія наступає разом з одною з подій , та . Застосуємо формулу повної ймовірності (18):

.

За умовою задачі умовні ймовірності , і . Тоді імовірність .

Шукану ймовірність знайдемо по формулі Байєса:

. ●

Схема Бернуллі: Якщо проводиться серія з випробувань, у кожному з яких можна спостерігати появу (або непояву) події так, що ймовірність появи цієї події в кожному випробуванні не залежить від наслідків інших випробувань цієї ж серії, то ймовірність того, що подія наступить у яких–небудь випробуваннях з визначається формулою Бернуллі

, (4.1.12)

де – ймовірність протилежної події ( ). Формула Бернуллі зручна лише для обчислень при порівняно невеликому числі випробувань ( ).

○ Приклад 4.1.8. Тест по теорії імовірностей складається з 10 запитань. На кожне запитання пропонується три відповіді, одне із яких правильне. Знайти ймовірність того, що студент, непідготовлений до тестів, правильно відповість: а) на чотири запитання; б) не менш чим на дев'ять запитань.

Розв'язання. Ймовірність того, що студент правильно відповість на запитання , а неправильно – . Тому що мало, то для обчислення ймовірності застосуємо формулу Бернуллі (4.3.12).

а) .

б) Подія – «студент відповість не менш чим на дев'ять запитань» можна представити як суму несумісних подій: , де – «студент відповість на дев'ять запитань» ( ) і – «на десять запитань» ( ).

Знайдемо ймовірністі:

і

.

Так як і , то шукана ймовірність

. Це практично неможлива подія. ●

Число настання події в незалежних випробуваннях називається найбільш ймовірним, якщо ймовірність здійснення цієї події не менше ймовірностей при будь–якому іншому , тобто для кожного .

Використовуючи формулу Бернуллі, можна одержати подвійну нерівність для визначення найбільш ймовірного значення :

. (4.1.13)

○ Приклад 4.1.9. Відомо, що 5% продукції, що випускає підприємство, не задовольняє вимогам стандарту. У магазин завезена партія з 100 виробів. Знайти найбільш ймовірніше число виробів, що не задовольняють вимогам стандарту.

Розв'язання. За умовою задачі , а ймовірність того, що виріб – нестандартний , тоді ймовірність того, що стандартне – . З формули (4.3.13) або . Єдине ціле число, що задовольняє отриманій нерівності, є . Це найбільш ймовірне число. ●

При великих серіях незалежних випробувань рекомендується замість (4.1.12) використовувати наближені формули:

1. Якщо велико, а – мало ( ), рекомендується використовувати наближену формулу Пуассона:

, (4.1.14)

де постійна величина .

2. Якщо велико, а – немало ( ), рекомендується використовувати локальну формулу (теорему) Лапласа

, (4.1.15)

де ; . Значення функції для різних додатних значень наведені в таблиці Д. 1 додатка.

Властивості функції : 1. є парною функцією, тобто ; 2. – монотонно спадна функція при додатних значеннях (вже за ).

Якщо потрібно обчислити приблизно ймовірність того, що подія відбудеться у випробуваннях не менш і не більше разів, то використовують інтегральну формулу (теорему) Лапласа

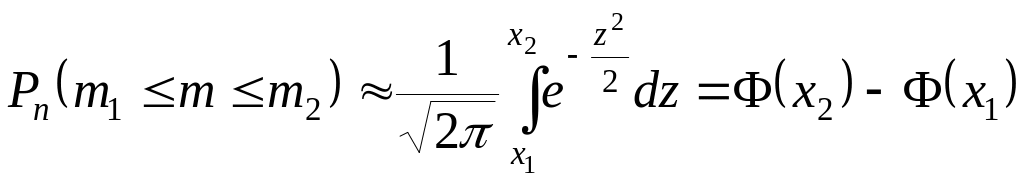, (4.1.16)

де й . – функція Лапласа (або нормована функція Лапласа). Значення функції наведені в таблиці Д. 2 додатка для різних додатних значень .

Властивості функції Лапласа: 1. є непарною функцією, тобто ; 2. – монотонно зростаюча функція при додатних значеннях (вже з ).

○ Приклад 4.1.10. Контрольне ревізійне управління перевіряє роботу 2000 підприємств області. Ймовірність виявлення неправильного оформлення бухгалтерських рахунків дорівнює 0,1. Знайти ймовірність того, що недоліки будуть виявлені на 240 підприємствах.

Розв'язання. За умовою задачі , , і . Застосуємо формулу (4.1.15).

Спочатку визначимо . Тоді ймовірність ,

де значення функції знайдене з таблиці Д. 1 додатка. ●

○ Приклад 4.1.11. З 1000 перевірених деталей 100 не задовольнять стандартам. Знайти ймовірність того, що серед 7000 перевірених деталей виявлять бракованих від 650 до 724.

Розв'язання. Ймовірність того, що деталь бракована – , а ймовірність того, що вона стандартна – . Застосуємо формулу (4.1.16), де і .

Спочатку визначимо

і .

Тоді ймовірність

, де , тому що функція Лапласа – непарна. У таблиці Д.2 додатка знайдемо та . ●

З формули (4.1.16) можна розрахувати ймовірність того, що абсолютна величина відхилення відносної частоти появи події від ймовірності не перевищить додатне число . Ця ймовірність приблизно дорівнює подвоєної функції Лапласа при , тобто

. (4.1.17)

○ Приклад 4.1.12. Ймовірність зриву поставки сировини на підприємства галузі по кожному дню дорівнює 0,2. Знайти число днів , коли з ймовірністю 0,998 можна чекати, що відносна частота появи події «зрив поставок» відхилиться від не більше ніж на 0,03 (по абсолютній величині).

Розв'язання. За умовою задачі , , і .

Застосуємо формулу (4.3.17): .

З таблиці Д. 2 додатка знайдемо .

Вирішимо рівняння . Звідси . – ціле число, тому маэмо . ●