Моделювання недетермінованого скінченного автомата.

Скінченні автомати широко використовуються на практиці, наприклад в синтаксичних і лексичних аналізаторах.

Недермінований скінченний автомат – це абстрактна машина, яка читає символи із вхідного ланцюжка і вирішує, допустити чи відкинути цей ланцюжок. Автомат має декілька станів і завжди знаходиться в одному з них. Він може змінити стан, переходячи з одного стану в інший. Внутрішню структуру такого автомату можна представити графом переходів, як показано на малюнку . У цьому прикладі S₁, S₂, S₃ і S₄ – стани автомата. Стартувавши із початкового стану (у нашому прикладі це S₁), автомат переходить із стану в стан у міру читання вхідного ланцюжка.

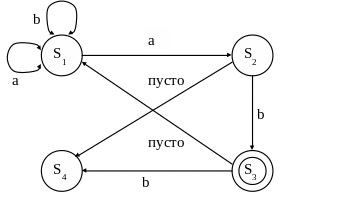
Рис 4. Приклад недетермінованого скінченного автомата.

Перехід залежить від поточного вхідного символу, як показують мітки на дугах графа переходів.

Перехід виконується кожен раз при зчитуванні вхідного символа. Зазначимо, що переходи можуть бути недетермінованими. На Рис 4. видно, що якщо автомат знаходиться у стані S₁ і поточний символ дорівнює a, то перехід може вібутися як в S₁, так і в S₂. Деякі дуги помічені міткою пусто, яка позначає «пустий символ». Ці дуги відповідають «спонтанним переходам» автомата. Такий перехід називається спонтанним, тому що він виконується без зчитування вхідного ланцюжка.

Стан S₃ обведений подвійною лінією, це означає, що S₃ – кінцевий стан. Про автомат кажуть,що від допускає вхідний ланцюжок, якщо в графі переходів існує шлях, такий, що:

1. він починається в початковому стані,

2. він закінчується в кінцевому стані, і

3. мітки дуг, які утворюють цей шлях, відповідають повному вхідному ланцюжку.

Вирішувати, який із можливих переходів робити в кожен момент часу – виключна справа автомата. Зокрема, автомат сам вирішує, чи робити спонтанний перехід, якщо він можливий в поточному стані. Однак абстрактні не детерміновані машини такого типу мають чарівну властивість: якщо існує вибір, вони завжди обирають «вірний» перехід, тобто перехід, який веде до допущення вхідного ланцюжка при наявності такого переходу. Автомат на малюнку, наприклад, допускає ланцюжки ab і aabaab , але відкидає ланцюжки abb і abba. Легко бачити, що цей автомат допускає всі ланцюжки, які закінчуються на ab і відкидає всі інші.

Деякий автомат можна описати на Пролозі за допомогою трьох відношень:

1. Унарного відношення final (кінцеве) , яке визначає кінцевий стан автомату.

2. Триаргументного відношення transition (перехід) , яке визначає перехід від стану до стану, при цьому transition(S1, X, S2) означає перехід від стану S1 до стану S2, якщо зчитаний символ X.

3. Бінарного відношення spontaneous(S1, S2) (спонтанний), яке означає,що можливий спонтанний перехід із S1 в S2.

Для автомата, зображеного на малюнку, ці відношення будуть такими:

final(S3).

transition(S1, a, S1).

transition(S1, a, S2).

transition(S1, b, S1).

transition(S2, b, S3).

transition(S3, a, S4).

spontaneous(S2, S4).

spontaneous(S3, S1).

Представимо вхідні ланцюжки у вигляді списків Прологу. Ланцюжок aab буде представлений як [a,a,b]. Модель автомата, буде обробляти заданий вхідний ланцюжок і вирішувати, допускати його чи ні. За визначенням, недетермінований автомат допускає заданий ланцюжок, якщо (починаючи із початкового стану) після її зчитування він здатен опинитися у кінцевому стані. Модель програмується у вигляді бінарного відношення permissible (допускається), яке визначає прийняття ланцюжка із данного стану. Так

permissible(State, Chain)

істинне, якщо автомат, починаючи із стану State як із початкового, допускає ланцюжок Chain. Відношення permissible можна визначити за допомогою трьох речень. Вони відповідають наступним трьом випадкам:

1. Пустий ланцюжок [ ] допускається із стану S , якщо S - кінцевий стан.

2. Непустий ланцюжок допускається із стану S, якщо після зчитування першого його символа автомат може перейти до стану S1, і частина ланцюжка, що залишилася, допускається із S1. Цей випадок ілюструється на рис. 5(а).

3. Ланцюжок допускається із стану S, якщо автомат може зробити спонтанний перехід із S в S1, а потім допустити (увесь) вхідний ланцюжок із S1. Цей випадок ілюструється на рис. 5(б).

перший символ

частина ланцюжка,що залишилася

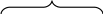
S

S₁

(б)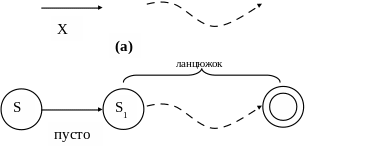

Рис. 5 Допущення ланцюжка: (а) при зчитуванні першого символа ; (б) при здійсненні спонтанного переходу.

Ці правила можна перекласти намову Пролог наступним чином:

permissible(S, [ ]):-

final(S).

permissible(S, [X | Remaining ]):-

transition(S, X, S1),

permissible(S1, Remaining ).

permissible(S, Chain):-

spontaneous(S, S1),

permissible(S1, Chain ).

Спитати про те, чи допускається ланцюжок aaab , можна так: permissible(s1, [a,a,a,b]). Повністю програму на Visual Prolog можна представити таким чином:

domains

list = symbol *

database

final(symbol)

transition(symbol, symbol, symbol)

spontaneous(symbol, symbol)

predicates

nondeterm permissible(symbol, list)

clauses

final(s3).

transition(s1, a, s1).

transition(s1, a, s2).

transition(s1, b, s1).

transition(s2, b, s3).

transition(s3, b, s4).

spontaneous(s2, s4).

spontaneous(s3, s1).

permissible(S, [ ]):-

final(S).

permissible(S, [X | Remaining ]):-

transition(S, X, S1),

permissible(S1, Remaining ).

permissible(S, Chain):-

spontaneous(S, S1),

permissible(S1, Chain ).

goal

permissible(s1, [a,a,a,b]).

Програми на Пролозі часто виявляються здатними вирішувати більш загальні задачі, ніж ті, для яких вони спершу були створені. В нашому випадку ми спитати модель також про те, в якому стані повинен знаходитись автомат на початку роботи, щоб він допустив ланцюжок ab :

permissible(S, [a,b]).

Ми можемо спитати також «Які всі ланцюжки довжиною 3, допустимі із стану s1?»

permissible(s1, [X1,X2,X3]).