Лекция № 5

В B^-1

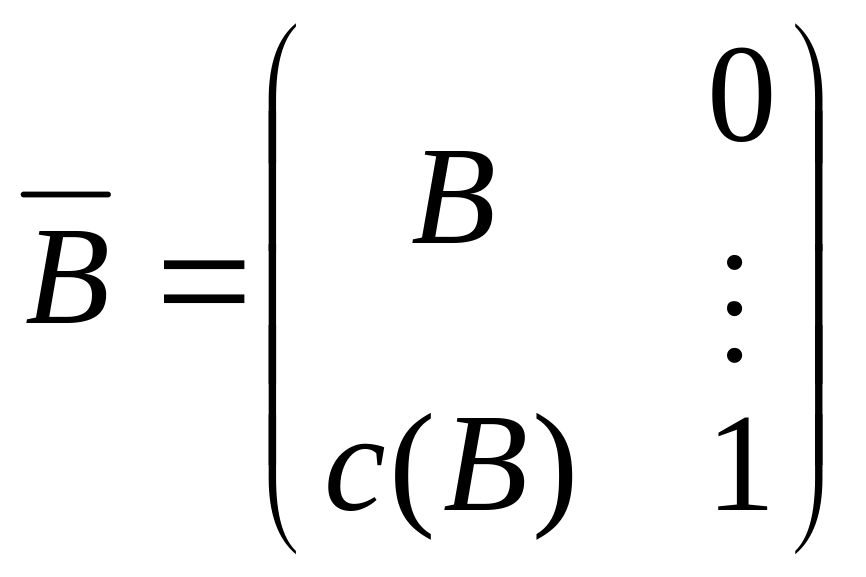
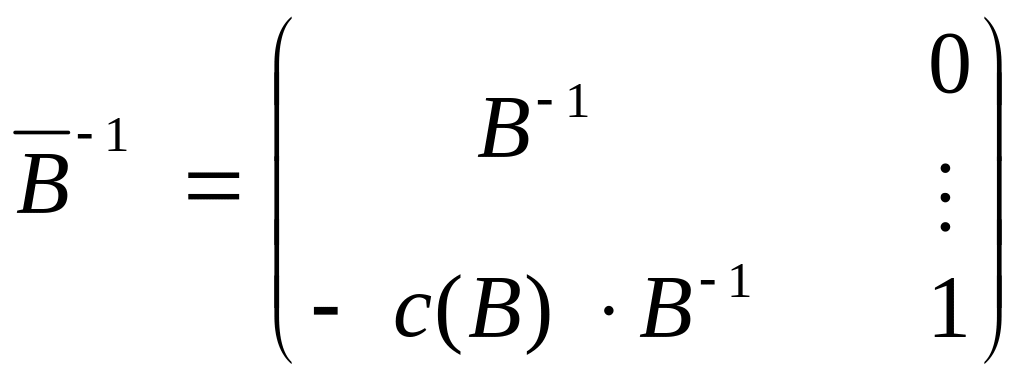
- расширенная матрица :

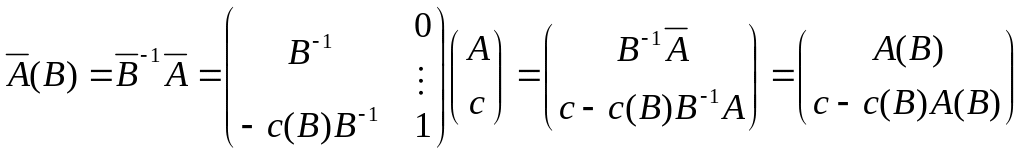
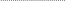. (1.42)

Для отдельных частей этой матрицы будем использовать следующие обозначения:

- i-ая строка,

- j-ый столбец,

- (i, j) – ый элемент.

Видим, что - это (m+1)´n–мерная матрица. Ее верхняя часть представляет собой уже известную матрицу A(B), а последняя строка этой матрицы

(1.43)

в линейном программировании называется строкой симплекс-разностей. Для этой строки также будем использовать следующее обозначение , где симплекс-разность, соответствующая j-ому столбцу (j-ой переменной) ЗЛП в соответствии с (1.43) равна

(1.44)

Сущность симплекс-разностей будет рассмотрена ниже при обосновании метода решения ЗЛП, называемого симплекс-методом.

1.5. Базисное решение системы основных ограничений злп

Основные ограничения ЗЛП, записанные в канонической форме ( ), можно рассматривать, как систему из m линейных уравнений относительно n неизвестных (причем n  m).

Пусть определен базис  и соответственно N(B), B, B^-1. Не снижая общности дальнейших рассуждений, предположим, что матрица условий представлена в виде двух следующих последовательно расположенных блоков:

А = (B D),

где D – m(n-m) – мерная матрица, в которую входят небазисные столбцы матрицы А. В таком виде матрицу А можно получить путем перестановки ее столбцов, не изменяя сущности задачи.

Вектор x, соответственно, представим состоящим из двух векторов:

,

где x' – (m) – мерный вектор базисных компонент вектора х,

x" – (n-m) – мерный вектор небазисных компонент вектора х.

Тогда основные ограничения можно представить в виде следующей системы уравнений:

( B D) .

Общее решение этой системы определяется следующим образом:

(1.45)

и зависит от значения вектора x", которое может быть выбрано произвольно.

Базисным решением ЗЛП, записанной в канонической форме, называется такое общее решение системы основных ее ограничений, которое получено при нулевом значении небазисных переменных (x" = 0).

Таким образом, можно утверждать, что базисное решение имеет не более чем m ненулевых (базисных) компонент. Для обозначения базисных компонент базисного решения используются обозначения x(B) или b(B):

, (1.46)

. (1.47)

Обозначения (1.46) будем использовать тогда, когда необходимо подчеркнуть связь значений базисных компонент с номерами компонент вектора x, а обозначение (1.47) – тогда, когда нам будут важны лишь только сами значения базисных компонент.

По аналогии с (1.40) можно утверждать, что базисные компоненты базисного решения являются коэффициентами разложения вектора правых частей основных ограничений по векторам базиса:

. (1.48)

Базисное решение называется допустимым решением ЗЛП (допустимым базисным решением) при условии

. (1.49)

Действительно, при выполнении неравенства (1.49) для базисного решения выполняются все ограничения ЗЛП (1.37), в том числе, и x  0.

Базис, определяющий допустимое базисное решение, будем называть допустимым базисом.

Базисное допустимое решение называется невырожденным, если выполняется строгое неравенство

. (1.50)

Если же некоторые базисные компоненты имеют нулевые значения, то такое базисное решение называется вырожденным.

В заключении введем в рассмотрение вектор

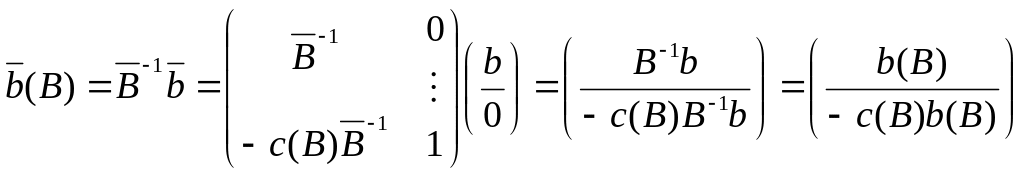. (1.51)

Таким образом, видим, что вектор – это (m+1) – мерный вектор-столбец, первые m компоненты которого совпадают с соответствующими компонентами вектора b(B), а последняя, (m+1)-ая компонента

(1.52)

представляет собой взятое с обратным знаком значение целевой функции ЗЛП, соответствующее базисному решению.