Министерство образования Российской Федерации

Саратовский государственный технический университет

ДИФРАКЦИЯ ЭЛЕКТРОНОВ

НА КРИСТАЛЛАХ

Методические указания

к выполнению учебно-исследовательской

лабораторной работы по курсу общей физики

для студентов всех специальностей

Одобрено

учебно-методическим семинаром

кафедры общей физики

Саратовского государственного

технического университета

Саратов 2011

ВВЕДЕНИЕ

В классической физике существует хорошо известное противопоставление свойств вещества и электромагнитного поля. Первым шагом на пути к единому описанию материи на микро уровне - было обнаружение и истолкование корпускулярно-волновых свойств света. Дальнейшее развитие единой физической картины мира связано с открытием волновых свойств у микрочастиц с ненулевой массой покоя - электронов, атомов и др.

В настоящее время идеи единого подхода к описанию и объяснению явлений окружающего нас мира являются общепризнанными, лежат в основе современной физики и составляют фундамент передовой техники и высоких технологий.

Описанные в данных методических указаниях лабораторные работы дают возможность студентам на примере электронов наглядно убедиться в проявлении волновых свойств микрочастиц.

Корпускулярно-волновой дуализм

Представления о квантовых (корпускулярных) свойствах света достаточно четко сформировались в физике к двадцатым годам XX века. Квантовые идеи использовали при рассмотрении теплового излучения, фотоэффекта, теплоемкости твердых тел. Особенно ярко корпускулярные свойства света проявилась в эффекте Комптона (открыт в 1923 г.). Одновременно, такие явления, как интерференция и дифракция, заставляли физиков приписывать свету волновую природу. Как остроумно заметил в то время Уильям Брегг, каждый физик должен был по понедельникам, средам и пятницам считать свет состоящим из частиц, а в остальные дни недели - из волн.

Лишь при объяснении некоторых явлений (например: прямолинейное распространение света, эффект Доплера) можно было с равным успехом следовать как той, так и другой теории. Это свойство света проявлять в одних экспериментах свойства частиц, а в других - свойства волн, получило название корпускулярно-волнового дуализма.

В 1923 - 1924 гг. французский физик Луи де Бройль выдвинул гипотезу о том, что дуализм корпускулярных и волновых свойств носит в природе универсальный характер и должен быть распространен не только на излучение (фотоны), но и на вещество (электроны). В своей Нобелевской лекции 1929 г. он изложил идеи, лежащие в основе дуализма, и требования общего подхода к теории излучения и вещества:

"С одной стороны, теория световых квантов не может быть признана удовлетворительной, потому что она определяет энергию корпускулы света соотношением W=h, в котором фигурирует частота . Однако чисто корпускулярная теория не содержит в себе ни одного элемента, который позволил бы определить частоту. Хотя бы по этой причине необходимо в случае света вводить одновременно и идею корпускулы и идею периодичности.

С другой стороны, определение стационарных движений электронов в атоме заставляет вводить целые числа, но до сих пор единственными явлениями в физике, при описании которых вводились целые числа, были явления интерференции и собственных колебаний".

Предположив, что частицы вещества, наряду с корпускулярными свойствами обладают также и волновыми, де Бройль перенес на частицы вещества связь волновых и корпускулярных свойств, установленных соотношениями Эйнштейна для фотонов:

, ,

, ,

где и - период и длина волны соответственно. В этих выражениях (энергия) и (импульс) - физические величины, характеризующие корпускулярные свойства объекта. Круговая частота и волновой вектор характеризуют периодичность во времени и пространстве, т.е. волновые свойства объекта, - постоянная Планка или элементарный квант действия - фундаментальная константа, величина которой зависит от выбора единиц измерения. Таким образом, согласно де Бройлю, длина волны , отвечающая частице массой , которая движется со скоростью , определяется формулой:

,

где h = 6.6210^-34 Джс, m- масса частицы, V- её скорость. Величину иногда называют дебройлевской длиной волны частицы.

Теория атома Бора (1913г.) показала, что взаимосвязь типа между возможными значениями энергии электронов в атоме и характерными для атома частотами является проявлением некой универсальной закономерности, а частоты - характеристиками каких-то волн, присущих электронам в атоме. Это подтверждали и эксперименты Франка и Герца (1913 г.) по рассеянию электронов на парах ртути.

В конце ХIХ в. были открыты и интенсивно изучались разного рода лучи. В газоразрядных трубках были обнаружены анодные, катодные и рентгеновские лучи. При исследовании явления радиоактивности открыты альфа-, бета- и гамма-лучи. Было установлено, что все лучи, кроме рентгеновских и гамма-лучей, переносят массу и электрический заряд. Причём величины масс и зарядов подчиняются принципу атомизма, т.е. наблюдаются только строго определенными порциями. По этой причине, в соответствии с экспериментально определенными отношениями заряда частицы к её массе, было признано, что анодные и альфа-лучи являются потоками частиц - положительных ионов, а катодные и бета-лучи - потоками электронов. Рентгеновские и гамма-лучи не обладали зарядом и массой, зато у них наблюдалась поляризация. Их стали считать электромагнитными волнами.

В качестве основного свойства, позволяющего отнести те или иные лучи к волнам или частицам рассматривалась способность лучей интерферировать. Уже в то время лабораторная техника позволяла осуществить эксперименты по дифракции электронов. Однако такие эксперименты до работ де Бройля не проводились. Слишком велика была уверенность в том, что электроны являются частицами и поэтому не способны к дифракции.

Возможность дифракции рентгеновских лучей была продемонстрирована при замене искусственно созданных дифракционных решеток естественными решетками - кристаллами (Макс фон Лауэ, 1912 г). Вместе с тем дифракция рентгеновских лучей на кристаллах служила прямым экспериментальным доказательством периодичности расположения атомов в кристаллах. С помощью этих естественных дифракционных решеток и была впоследствии обнаружена дифракция электронов.

КООРДИНАТЫ АТОМОВ И ПЛОСКОСТЕЙ В КРИСТАЛЛАХ

П

Рис.1. Участок рисунка обладающего трансляционной симметрией. “a” и “b” – векторы базиса.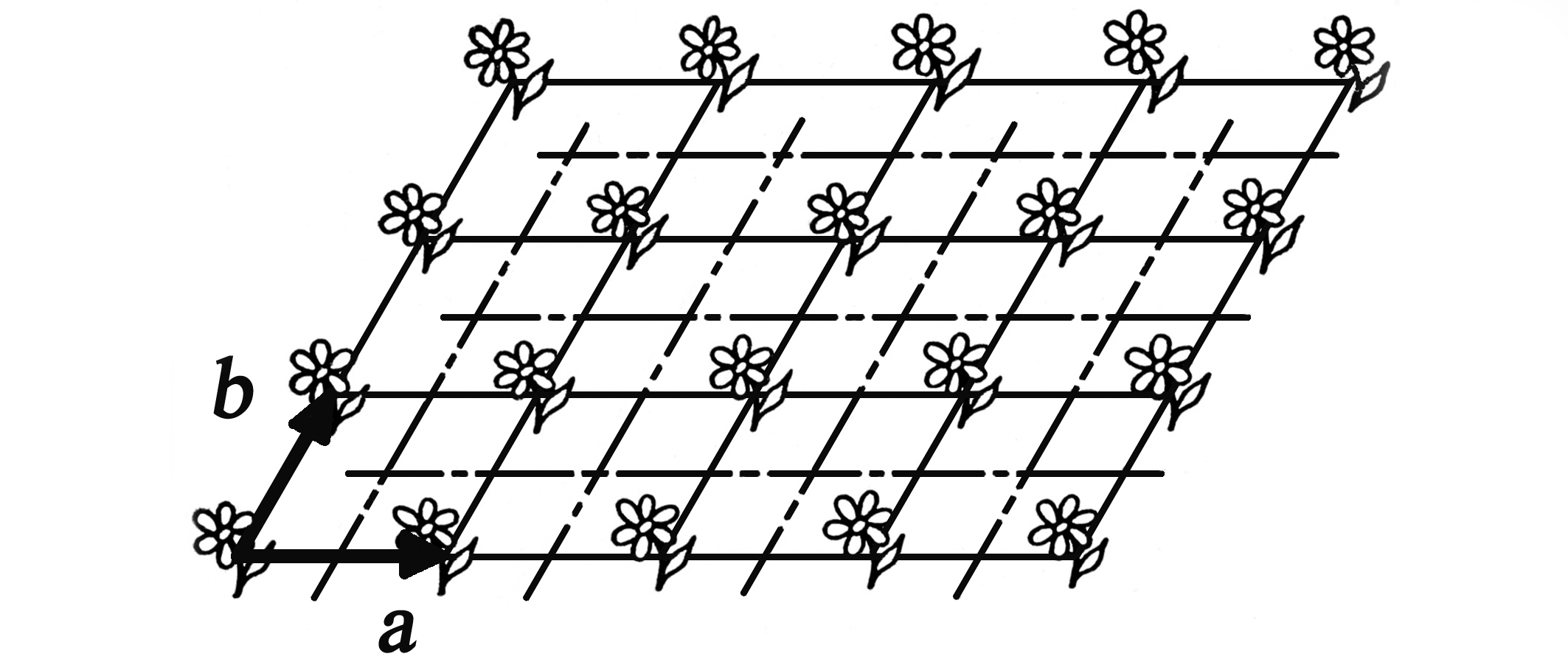

ериодичность расположения атомов в кристаллах принято харак­теризовать базисными векторами трансляций , , . Смещение атома на один из векторов трансля­ции или на целое число их длин переводит этот атом в положение, занятое точно таким же атомом. Свойства векторов трансляции позволяют определять всю пространст­венную решетку путем задания базиса. Возмож­ность этого для двухмер­ного случая продемонстри­рована на рис.1 на примере изображения участка обоев.

П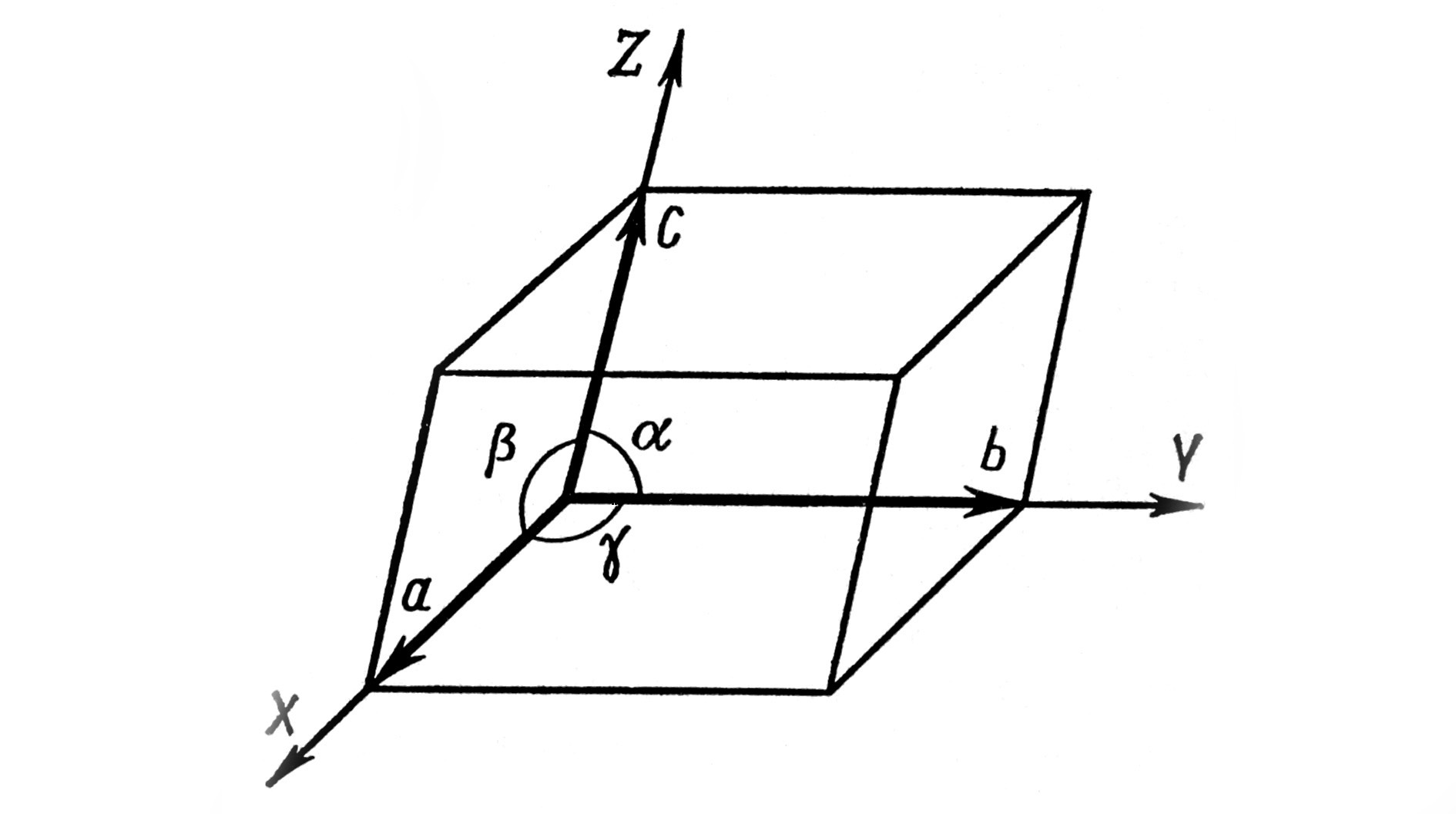 араллелепипед, построенный на трёх элементарных трансляциях a, b, c, называется элементарной ячейкой (рис.2). Здесь , ,  - углы, лежащие соответственно против осей X, Y, Z.

Э

Рис.2. Элементарная ячейка.

та идея лежит в основе кристаллографической системы координат. Оси системы направ-лены вдоль базисных векторов, а масштаб по осям выбирается равным длине соответствующего базисного вектора. На рис.3 показаны примеры координат некоторых атомов в кристаллографической системе координат.

Рис.3. Координаты некоторых атомов в кристаллографической системе координат.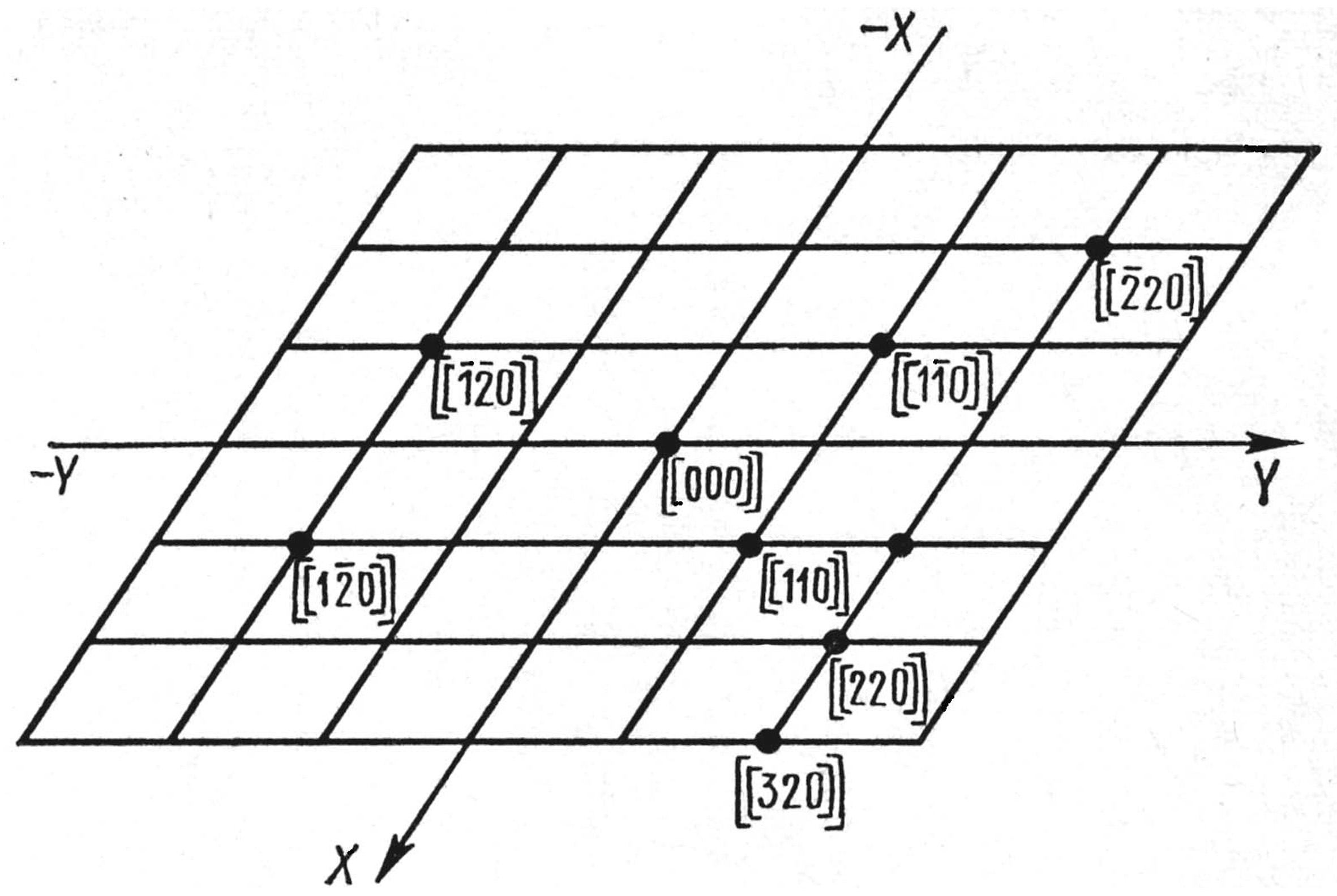

Если один из узлов решётки выбрать за начало координат, то любой другой узел решётки определяется радиусом-вектором:

,

где p, q, r - координаты атома, на котором оканчивается вектор.

Плоскость в такой системе координат задают величинами отрезков, отсекаемых этой плоскостью на осях. Например, в лабораторной прямоугольной системе координат с масштабами по осям X, Y, Z, равными соответственно a, b, c, уравнение плоскости в отрезках выглядит так:

Например, при x = 0, y = 0 плоскость отсечёт на оси Z отрезок rc. В кристаллографической системе координат для определения положения плоскости достаточно задать только числа p, q, r. Чтобы не использовать для определения параллельной какому-либо базисному вектору плоскости бесконечных значений индексов, принято для задания плоскостей применять индексы, обратные этим числам - индексы Миллера:

h=1/p, k=1/q, l=1/r.

В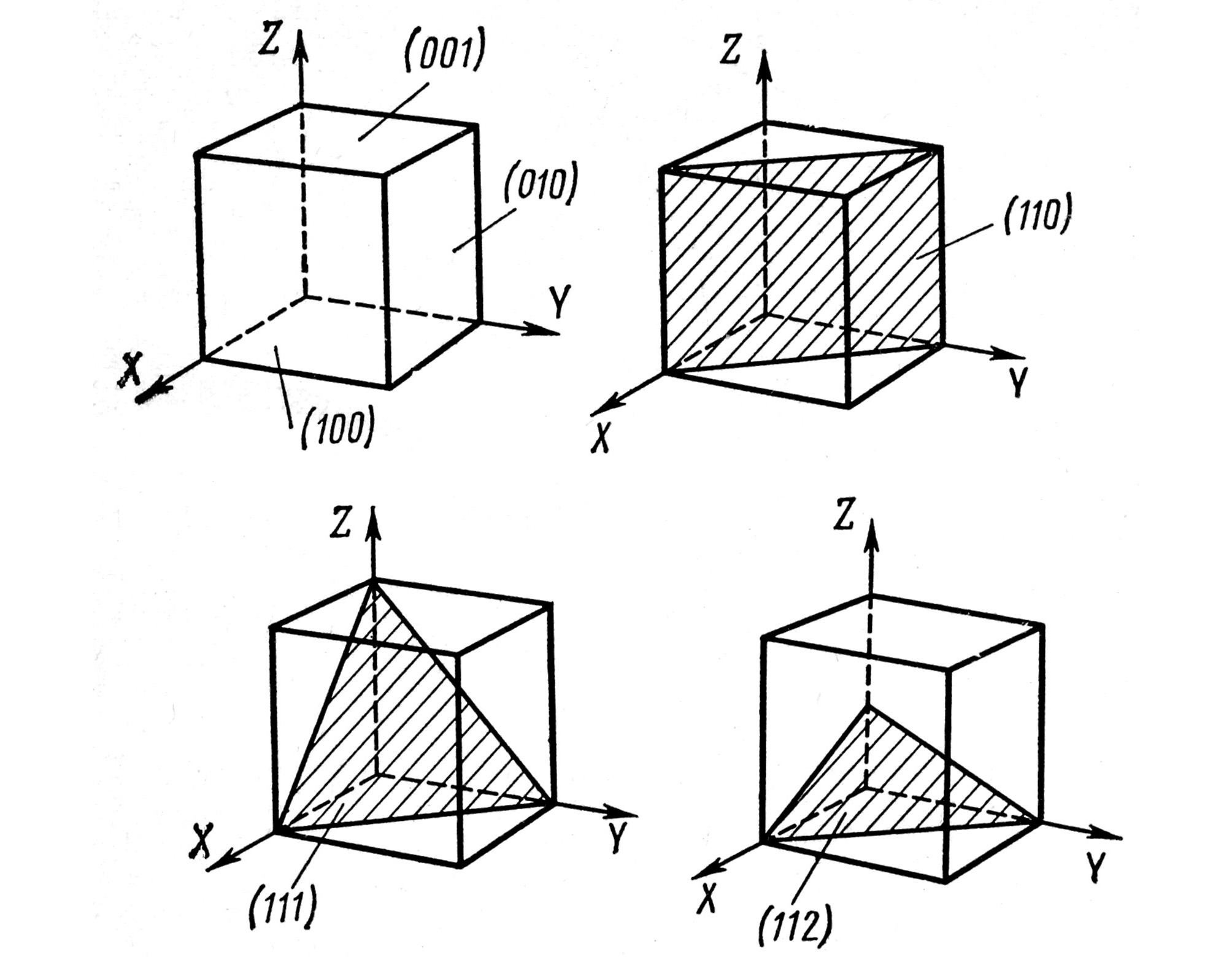 новых обозначениях плоскость в кристалле задается набором индексов Миллера (hkl). При этом, индексы параллельных друг другу плоскостей будут отличаться друг от друга на некоторое целое число. Поэтому весь набор эквивалентных друг другу с точки зрения дифракции плоскостей можно определить как {hkl}=(HKL), где H = mh, K = mk, L=ml, т - любое целое число. Примеры плос-костей и их индексы приведены на рис.4. Векторы , , направлены вдоль осей X, Y, Z, соответственно.

| | = | | = | | =1.

Рис.4. Примеры плоскостей и их индексы.