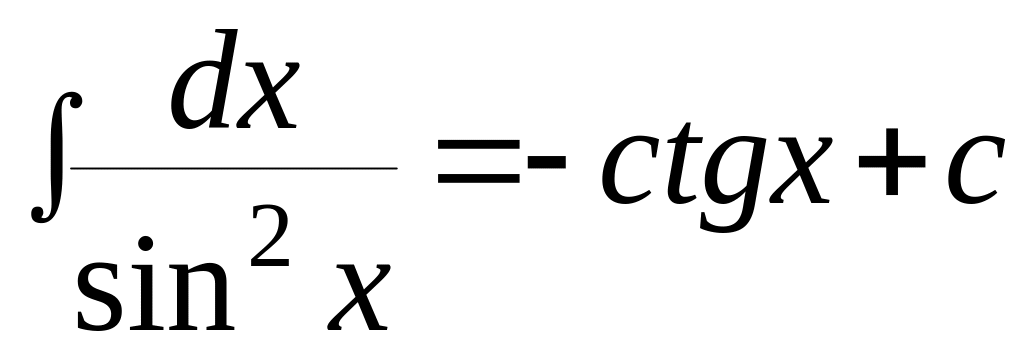Основные формулы интегрирования

(табличные интегралы)

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

Непосредственное интегрирование это такой способ, при котором интеграл путем тождественных преобразований подынтегральной функции и свойств неопределённого интеграла производится к одному или нескольким табличным интегралам.

Пример №1

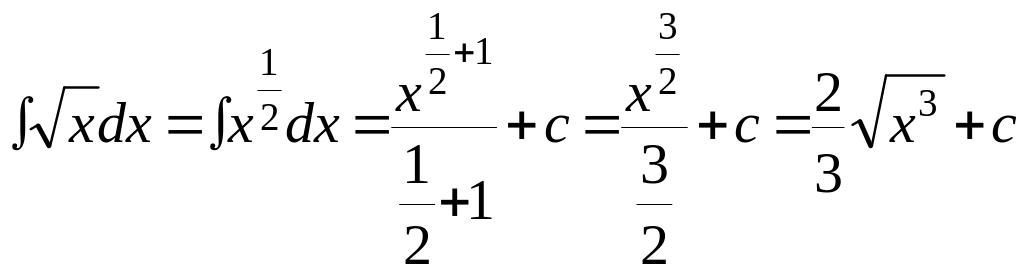
Пример №2

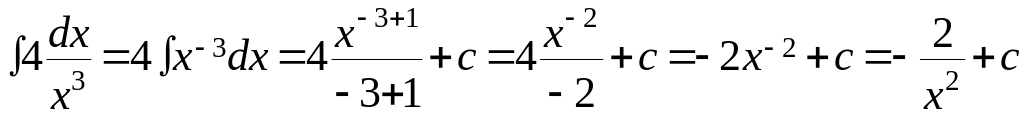
Пример №3

Пример №4

Пример №5

Интегрирование методом подстановки.

Сущность этого метода заключается в том, что путём введения новой переменной удаётся ввести данный интеграл к новому интегралу, который сравнительно легко берется непосредственно. Для интегрирования методом подстановки можно использовать такую схему.

1. Часть подынтегральной функции надо заменить новой переменной;

4. Найти дифференциал от обеих частей замены;

5. Всё подынтегральное выражение выразить через новую переменную

6. Найти полученный табличный интеграл.

7. Сделать обратную замену.

Примеры:

1. 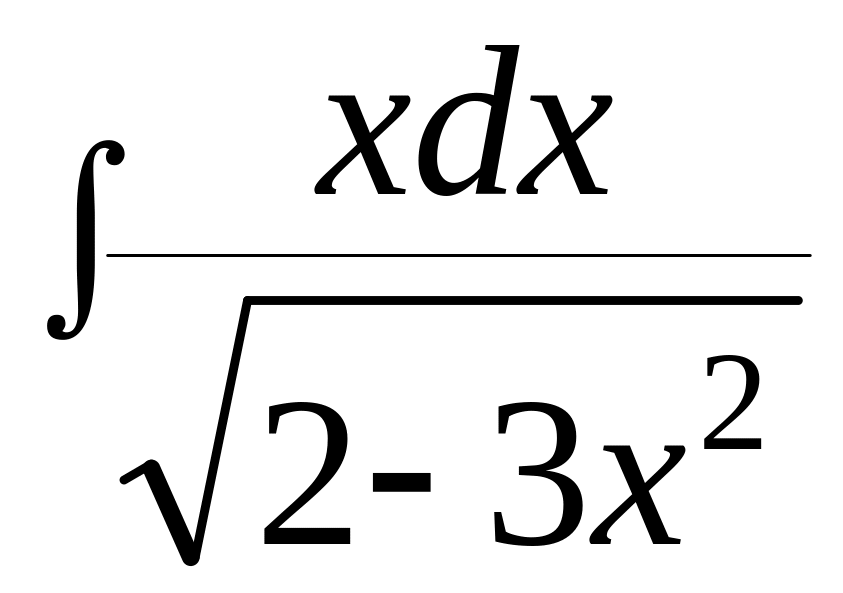пусть тогда

или подставим

2. 

пусть , тогда или получим

2. 

пусть тогда или получим

2. пусть тогда или подставляем в интеграл

Вопросы для самопроверки:

1. Какое действие называется интегрированием.

2. Какая функция называется первообразной?

3. Дайте определение неопределённого интеграла.

4. Вспомните свойства неопределённого интеграла

5. Каким действием можно проверить интегрирование.

6. Напишите основные формулы интегрирования.

7. Найдите интегралы:

Ответы:

а) а)

б) б)

в) в)

г) г)

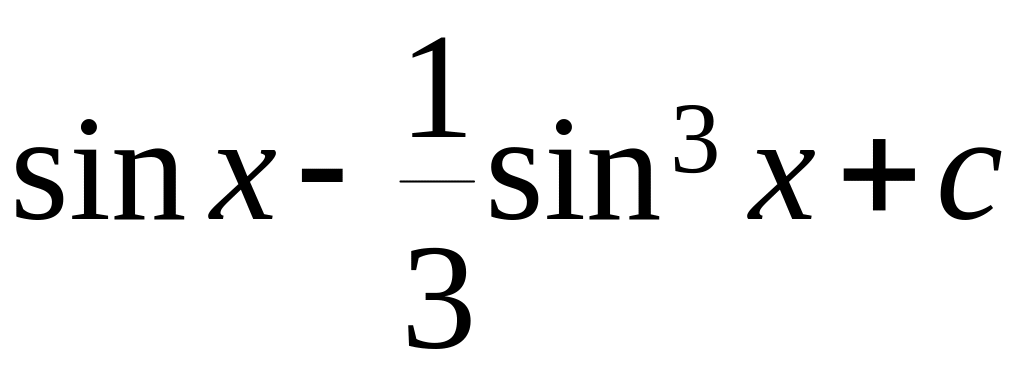
Определённый интеграл.

Напомним, что приращением аргумента x при его изменении от до называется разность , а приращением функции при изменении аргумента от до называется разность .

Если - первообразная функции, для , то приращение первообразных функций при изменении аргумента x от x=a до x=b называется определённым интегралом и обозначается символом , т.е. и читается так: “определённый интеграл от а до в эф от икс дэ икс ”

Формула называется формулой Ньютона – Лейбница свойства определённого интеграла:

1. Определённый интеграл с одинаковыми пределами равен нулю:

2. При перестановке пределов интегрирования знак интеграла меняется на противоположный:

3. Постоянный множитель можно выносить за знак интеграла

4. Отрезок интегрирования можно разбить на части:

, где

5. Интеграл от алгебрaичeской суммы функций равен такой же алгебраической сумме интегралов от всех слагаемых:

Порядок вычисления определённого интеграла:

1. Найти неопределённый интеграл от данной функции;

2. В полученную первообразную подставить вместо аргумента сначала верхний, затем нижний предел интегрирования.

3. Из результата подстановки верхнего предела вычесть результат подстановки нижнего предела.

Пример №1

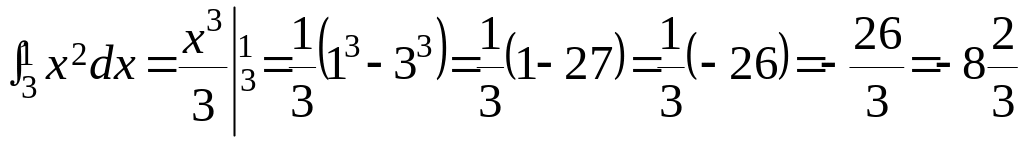
Пример №2

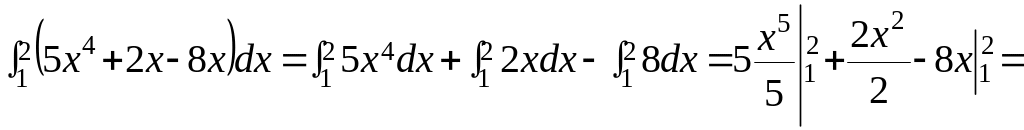
Пример №3

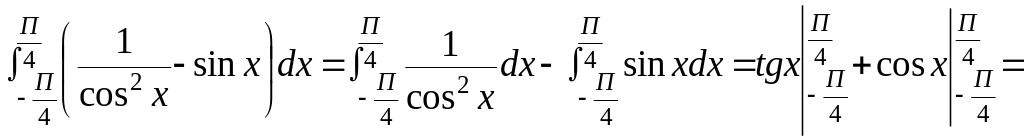
Вычисление определённого интеграла методом подстановки.

Состоит в следующем:

1. Часть подынтегральной функции заменить новой переменной.

2. Найти новые пределы определённого интеграла

3. Найти дифференциал от обеих частей замены

4. Все подынтегральное выражение выразить через новую переменную

5. Вычислить полученный определённый интеграл

Пример №1

Вычислить

Решение: Пусть , тогда , т.е.

Если , ; , значит,

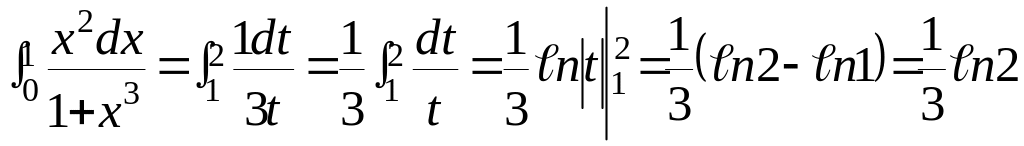
Пример №2

Решение.

значит

Пример №3

значит

Пример №4

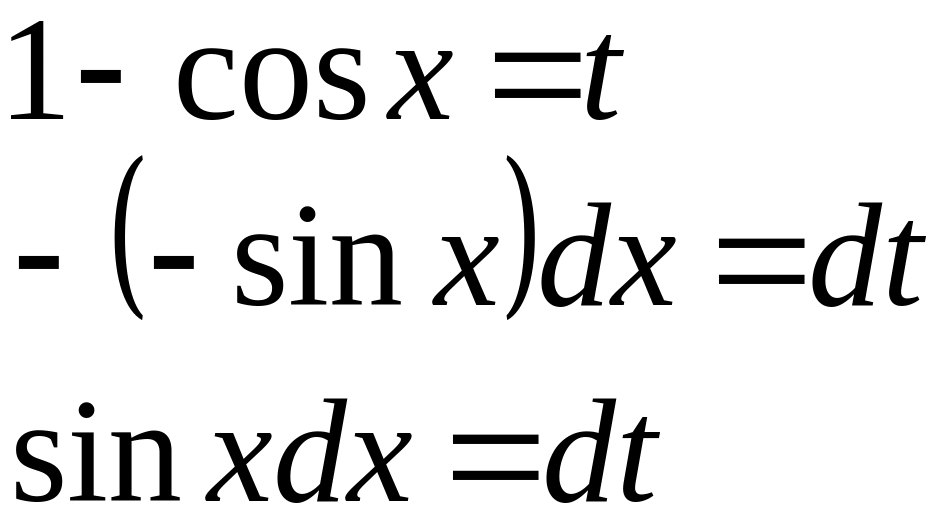
значит.

Вычисление площадей фигур с помощью определённого интеграла.

Задачи на вычисление площадей плоских фигур удобно решать по следующему плану:

1. По условию задачи делают чертёж.

2. Представляют искомую площадь как сумму или разность площадей криволинейных трапеций.

3. Определяют пределы интегрирования.

4. Записывают каждую функцию в виде

5. Вычисляют площади каждой криволинейной трапеции и площадь искомой фигуры.

Пример 1

Вычислить площадь фигуры, ограниченной параболой

, прямыми и осью абсцисс.

Y Решение:

-1 2 x

Пример 2

и

Построим прямую

;

Построим прямую

Найдём точку пересечения прямых для этого решим систему

x-2y+4=0

D(0;5)

y

-3y+9=0 x+y-5=0

т.е M(2;3)

М

C(5;0)

A(-4;0) 0 N(2;0)

Найдём площади треугольников AMN и NMC

Пример 3

и

точки пересечения параболы с осью ох; и

y

На отрезке график 0 x

функции расположен

ниже оси ох. Следовательно

Вопросы и упражнения для самопроверки.

1. Дайте определение определённого интеграла.

2. Перечислите основные свойства определённого интеграла.

3. Напишите формулы для определения площади плоской фигуры с помощью определённого интеграла.

4. Вычислите определённые интегралы:

; ; ;

5. Вычислите площадь фигуры, ограниченной линиями:

а) ; ; ;

б) и

в) и