Определение передаточных отношений в составных редукторах

Составными или сложными будем называть механизмы передачи вращательного движения, включающие в свой состав помимо простых передач планетарные или дифференциальные передачи.

П ри определении передаточных отношений в составных редукторах общее передаточное отношение определяется как произведение передаточных отношений всех последовательно соединённых передач. При этом планетарная (или дифференциальная) передача рассматривается как одна промежуточная передача.

Определим общее передаточное отношение составного редуктора, приведённого на рисунке 6. Редуктор состоит из последовательно соединённых передач: 1-2 – простая передача, 3-Н – планетарная передача, 7-8 – простая передача. Из кинематической схемы редуктора видно, что ₂=₃, _н=₇.

Таким образом общее передаточное отношение запишется в виде:

.

Для определения передаточного отношения планетарного механизма необходимо воспользоваться методом Виллиса.

Для определения количества элементов планетарной (или дифференциальной) передачи необходимо руководствоваться следующим правилом.

Планетарный (или дифференциальный) механизм включает в себя водило; звенья, которые переносит водило (сателлиты) и колеса, которые входят в непосредственное зацепление с сателлитами.

В нашем примере это водило Н, сателлит 4-5 и колёса 3 и 6.

Рассмотрим ещё одну особенность при определении передаточных отношений в планетарных механизмах. Предположим, что нам необходимо определить передаточное отношение от звена 8 к звену 1. В общем виде запишем:

.

При определении методом обращения, получим:

.

Полученное выражение неудобно для преобразования. Поэтому в этом случае нужно воспользоваться величиной, обратной :

; .

Формула для определения общего передаточного отношения принимает вид:

.

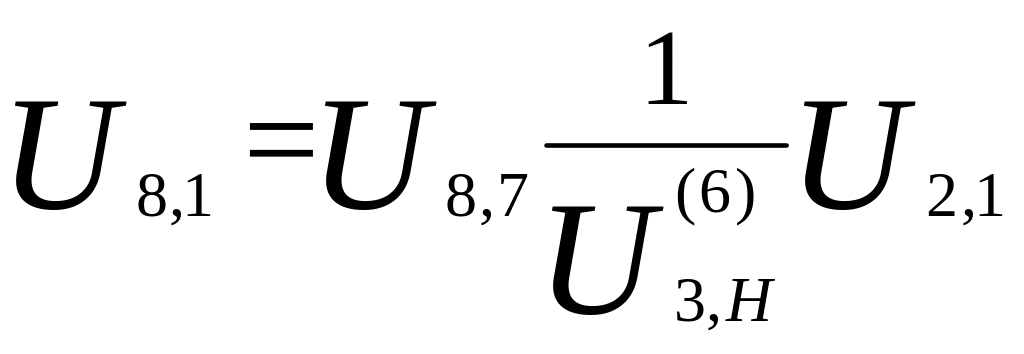Дальше задача решается известными методами.

По сравнению с простыми передачами планетарные механизмы имеют ряд преимуществ. В основном они используются в тех отраслях промышленности, где необходимо при небольших габаритах передачи получить большие передаточные отношения. При этом планетарные передачи имеют значительно меньшие весо-габаритные показатели по сравнению с обычными передачами.

Рассмотрим конкретный пример. Определим передаточное отношение планетарной передачи, изображенной на рисунке 3а (редуктор Девида). Этот пример характеризует одно из преимуществ планетарного механизма – получение большого передаточного отношения при малом числе зубчатых колёс и малых размерах колёс.

Примем количества зубьев: z₁=20, z₂=19, z_2’=20, z₃=21.

Определим передаточное отношение в обращённом механизме от звена 1 к звену 3:

.

В обычном редукторе скорость выходного вала изменилась бы на незначительную величину .

Воспользуемся формулой Виллиса для планетарных механизмов и определим передаточное отношение от звена 1 к водилу Н:

.

Введя дополнительный элемент (водило) в редуктор мы изменим скорость выходного звена редуктора в 400 раз.