Червячная передача

Ч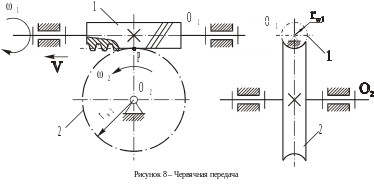 ервячные передачи применяются для передачи вращательного движения между двумя горизон­тальными скрещивающимися осями. Червячная передача содержит два вращающихся элемента: червяк - как правило, это ведущее звено, червячное колесо - ведомое звено. Геометрия зацепления червячной пары сложная, но условное изображение простое (рисунок 8).

Основными параметрами, характеризующими червячную пару, являются: заходность червяка - k и количество зубьев червячного колеса - Z. Червяк-винт. Заходность червяка - это число независимых винтовых­ниток на поверхности червяка. Если червяк рассечь плоскостью перпендикулярной к оси вращения червяка, то пересечем столько витков, сколько заходов имеет червяк. В технике применяются 1, 2, 3 и 4^х заходные червяки. Червяки с большим числом заходов не экономичны вследствие больших потерь мощности на трение (повы­шенный нагрев при работе).

Нарезка винтовых линий может быть правая (слева - вверх - направо) и левая. У нас на схеме изо­бражен левый 3^х заходный червяк. Определим передаточное отношение червячной пары:

.

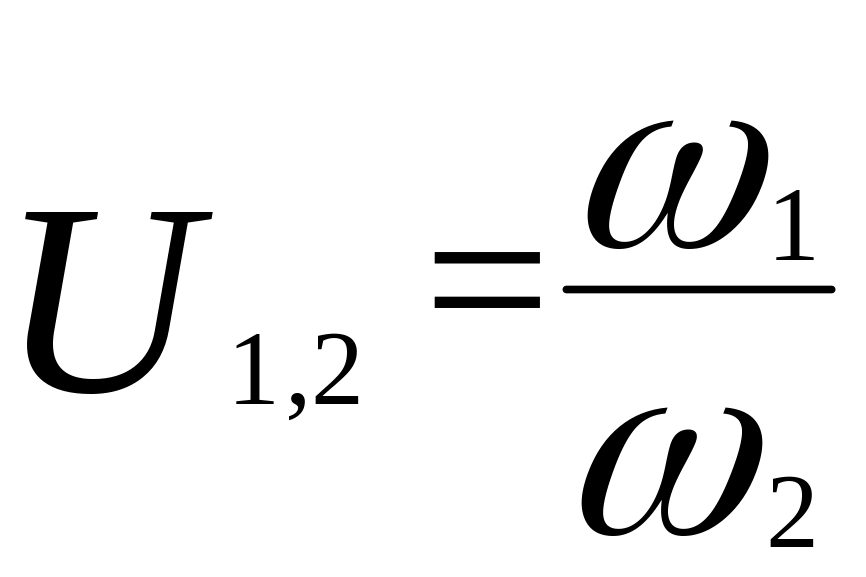Рассечем червяк осевой плоскостью. В плоскости сечения получим зубчатую рейку. Будем вращать червяк с угловой скоростью ₁. Сечение при этом будет смещаться со скоростью V.

Начальная окружность червячного колеса - это условная окружность, точки которой имеют линей­ную скорость, равную скорости смещения сечения червяка - V.

Если повернуть червяк на угол ₁=2, то червячное колесо повернется на число зубьев, равное за­ходности червяка k. Угол поворота червячного колеса при этом составит:

,

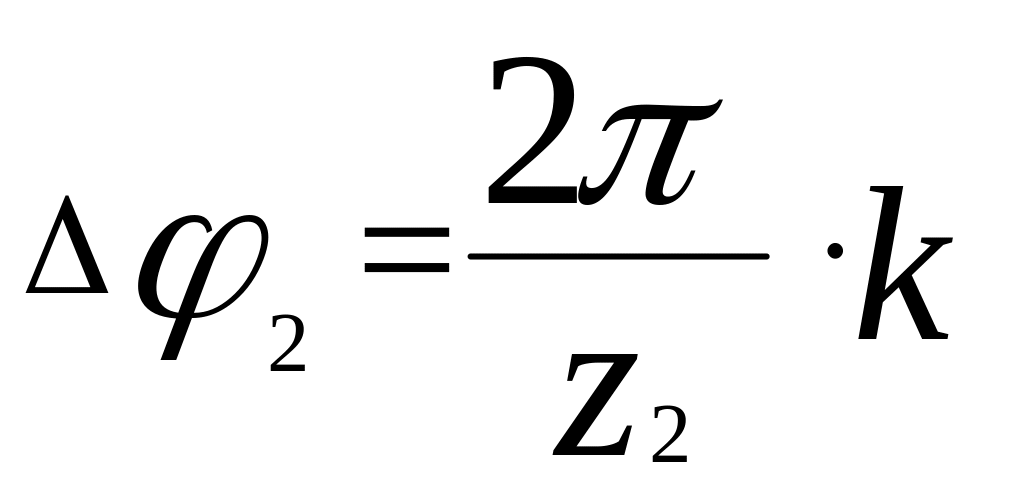где 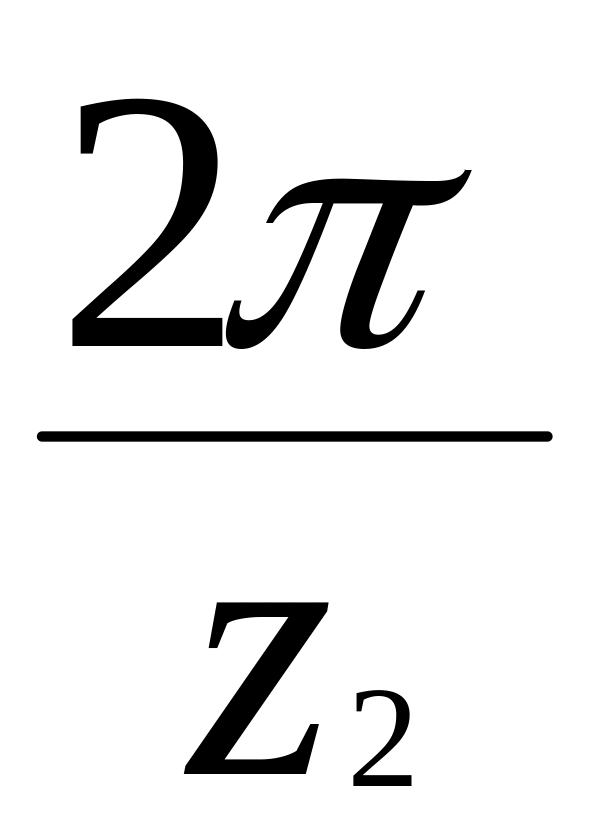- угловой шаг червячного колеса.

Определим средние угловые скорости червяка и червячного колеса. Пусть мы повернули червяк на один оборот за время t, тогда:

, .

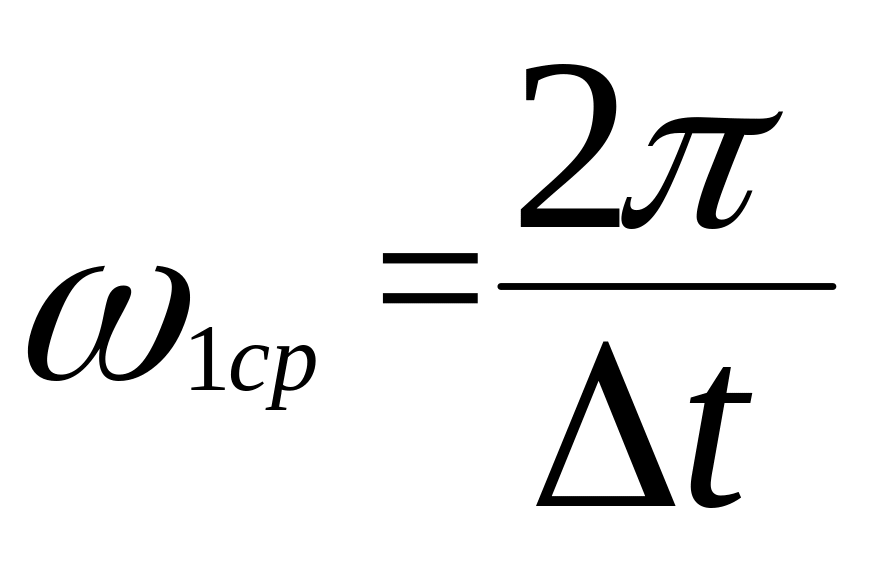При определении передаточного отношения мы имеем ввиду отношение мгновенных угловых ско­ростей:

.

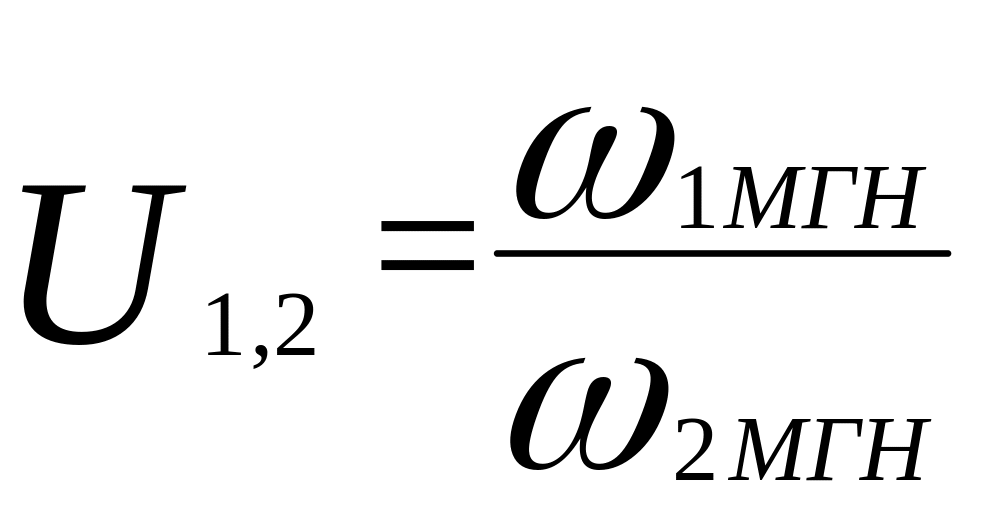Если геометрия червячной пары постоянна (const), то средние скорости за любой промежуток вре­мени одинаковы. Это значит, что если менять скорость червяка, то по такому же закону будет меняться угловая скорость червячного колеса, и передаточное отношение в этом случае будет величиной постоянной:

.

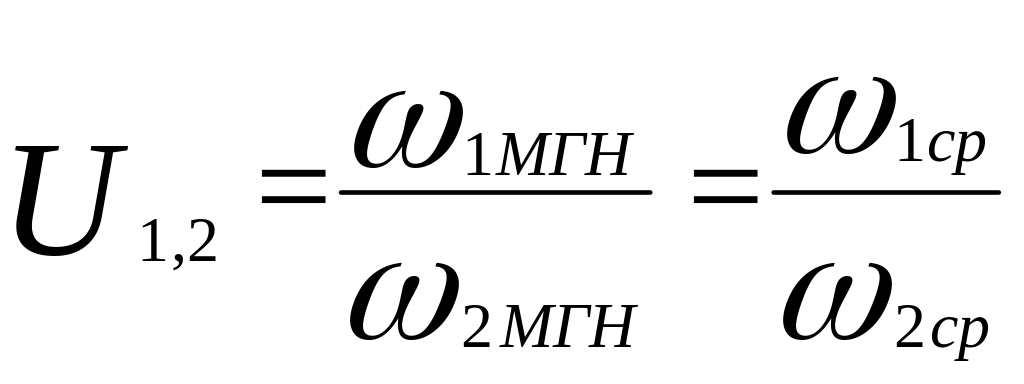Подставим в это выражение значения средних угловых скоростей червяка и червячного колеса:

.

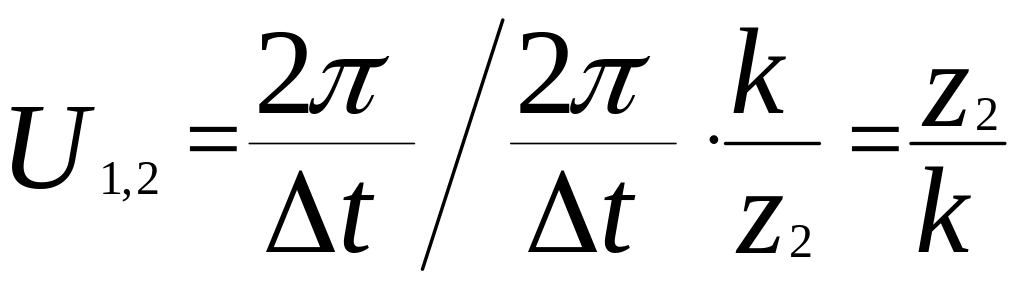Передаточное отношение червячной пары равно отношению чисел зубьев колеса к заходности червяка. Из по­лученной формулы видно, что червячная пара может иметь большое передаточное отношение. Например при k=1, Z₂=50 - U_1,2=50. В обычной зубчатой передаче такое передаточное отношение можно получить только по­следовательным соединением нескольких передач. В реальных условиях червячное колесо не может быть вы­полнено с числом зубьев более 120. Это связано с условиями нарезания зубчатых колес.

Наряду с указанным преимуществом червячные передачи имеют существенный недостаток - низкий коэффициент полезного действия. Большие потери мощности происходят в червячной передаче из-за наличия трения в паре червяк - колесо. Это приводит к повышенному нагреву механизма, быстрому износу червячной пары.