Для релятивистских частиц ≈1 величина q перестает зависеть от энергии частицы:
,
а число δ-электронов с энергией Тe (МэВ) в интервале (Тe, Тe+dТe), созданных в среде на пути в 1 г/см2 релятивистской частицей, получается равным:
Из этой формулы видно, что число δ - электронов с энергией Тe , образованных в 1 г/см2 вещества релятивистской частицей, прямо пропорционально квадрату заряда частицы z2 и практически не зависит от характеристик среды, так как Z/A ≈ 0,5. Отсюда следует, что по плотности δ - электронов на треке частицы (например, в пузырьковой или фотоэмуль- сионной камере) можно определить заряд z релятивистской частицы.
Чтобы найти полное число δ-электронов на единице пути частицы (плотность δ-электронов), надо проинтегрировать по всем возможным энергиям δ-электронов Те от минимальной до максимальной:
-
некоторая нижняя граница δ-электронов,
которая может быть выбрана довольно
произвольно, но при условии, что δ-
электроны все же могут сами ионизовать.
Часто, например, принимают величину
минимальной энергии
Максимальная энергия, которую может получить электрон при столкновении с ним частицы массы М и кинетической энергией Е, будет:
,
и, если M >> me,
.
Подставляя значения
и
найдем
плотность -электронов
на 1 г/см2 пути:
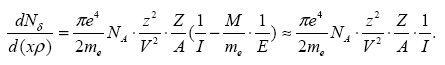
Угловое распределение
Задача решается с точки зрения упругого рассеяния первичной частицы
на свободных электронах.
В системе центра инерции (СЦИ) угловое распределение δ-электронов определяется формулой Резерфорда: V – скорость налетющей частицы.
Преобразование этой формулы от интервала
углов (
)
к соответствующему интервалу углов в
л.с. можно воспользоваться соотношением
ψ
= (π-
)/2,
где ψ
– угол вылета δ-электрона
относительно направления движения
частицы.
Эту формулу можно получить из векторной диаграммы импульсов и из законов сохранения энергии.
Отсюда 
Преимущественное направление вылета δ-электронов ψ ~ π/2. по отношению к направлению движения первичной частицы.
Энергия, переданная заряженной частицей δ – электрону,
связана с углом его вылета соотношением:
при M>>me/
Таким образом δ-электроны, вылетающие под малыми углами к траектории частицы
(ψ~0), имеют максимальную энергию,
а вылетающие под углами, близкими к π/2, имеют энергии минимальные. Зная
энергию δ – электрона (например, по пробегу) и угол его вылета ψ
можно оценить энергию частицы Е.