2.2.3. Подбор чисел зубьев планетарного редуктора

Передаточное отношение планетарного редуктора:

Схема механизма:

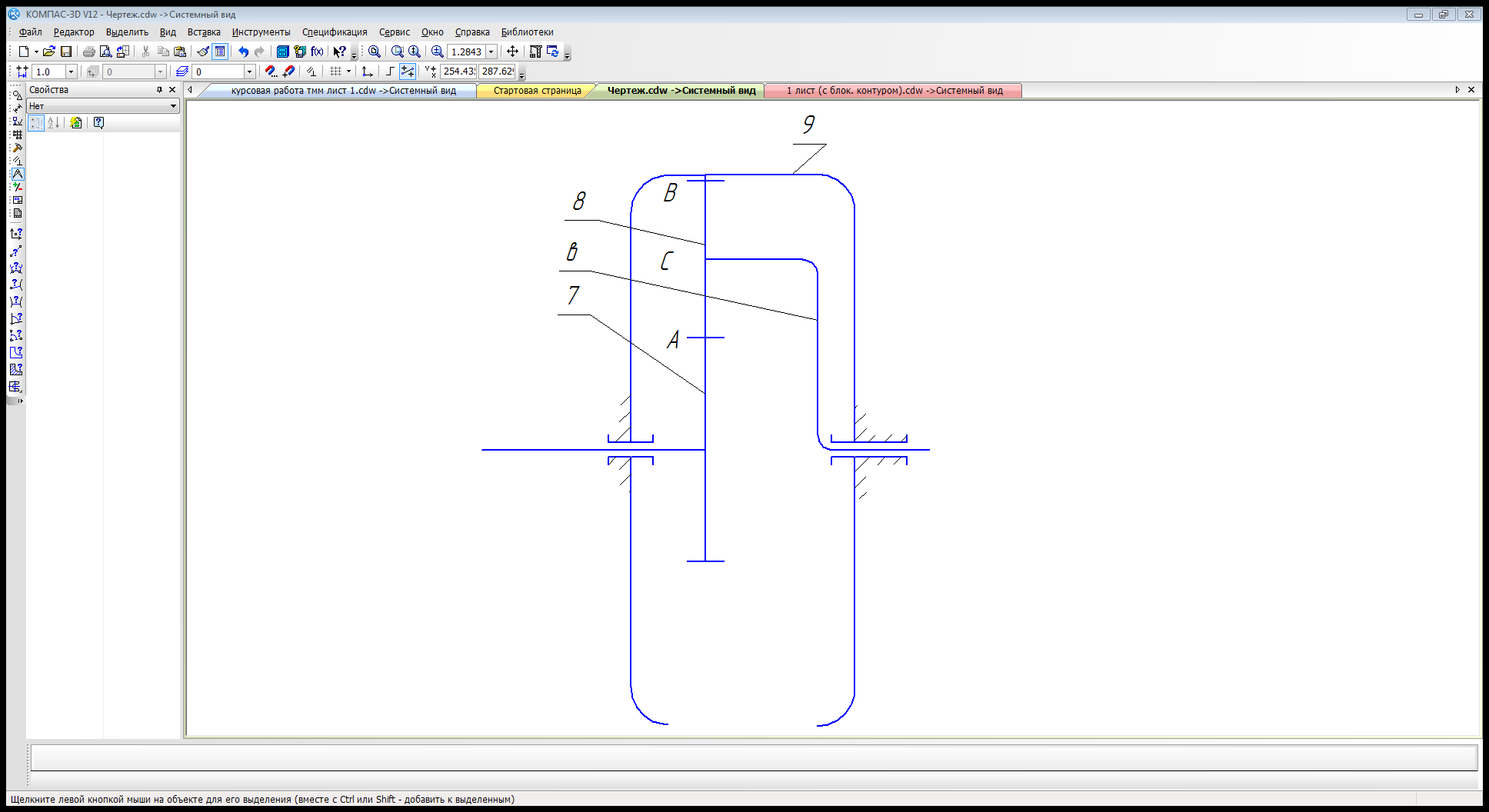
При подборе чисел зубьев учитываются ограничения накладываемые отсутствием подреза:

; внутреннее зацепление малое колесо

; внутреннее зацепление большое колесо

; внешнее зацепление

Т.е. для однорядного планетарного редуктора со смешенным зацеплением

; ;

Подберем число зубьев, учитывая все условия, накладываемые на многосателлитные редукторы:

1. Формула Виллиса: ;

2. Условие соосности: ;

3. Условие сборки: ;

4. Условие совместимости:

При P=33 Z₇ – любое целое цисло.

Число зубьев находим перебором. Первое условие: Z₇ должно быть больше 17. Второе условие Z₉ должно быть больше 85, используя формулу Виллиса получаем выражение для Z₉=U_1в-1*Z₇. Таким образом находим пару чисел 40 и 96. Пара подходит и получаем, что Z₈=28.0,

Z₇=40, Z₈=28, Z₉=96.

Проверка условия соосности:

40+28=96-28; 68=68; верно.

Проверка условия совместимости:

верно.

В результате расчета подобраны числа зубьев колес однорядного планетарного редуктора со смешанным зацеплением, удовлетворяющие всем условиям. Накладываемым на многосателлитные редукторы:

Z₇=40, Z₈=28, Z₉=96.

2.2.4. Графическая проверка передаточного отношения

1. Расчет радиусов колес планетарного редуктора:

Где r_i – радиус i^ого колеса редуктора,

m – модуль.

2. Построение схемы планетарного редуктора в масштабе .

3. Проверка передаточного отношения (графически из распределения линейных скоростей).

Для построения распределения линейных скоростей на схеме редуктора отмечаются характерные точки: центры колес и точки зацеплений. Все отмеченные точки выносятся на вертикальную ось радиусов.

Откладываем отрезок AA’=80мм в масштабе Отрезок OA’- линию распределения скоростей 1 звена (лрс1). Скорость V_C =0. Строим линию распределения скоростей блока сателлитов (лрс2-3). Строим отрезок BB’=40мм, в масштабе . Скорость точки B=10м/с. Отрезок OB’- линия распределения скоростей водила (лрсв).

,

,

,

,

.

4. Проектирование передаточного отношения (графически из плана угловых скоростей).

Для построения плана угловых скоростей проводим горизонтальную линию угловых скоростей. Выбираем полюс р на расстоянии 37 мм от нее, проводим из него лучи параллельные линиям распределения скоростей до пересечения с осью. Отрезки ka_в, ka₁, ka_2-3 выражают в масштабе угловые скорости соответствующих звеньев.

,

,

,

.

2.2.5. Выводы

1. В результате расчета подобраны числа зубьев колес двухрядного планетарного редуктора со смешанным зацеплением, удовлетворяющие всем условиям, накладываемым на многосателлитные редукторы:

2. Z₇=40, Z₈=28, Z₉=96.

3. Передаточное отношение проверено графически с помощью графиков угловых и линейных скоростей. Погрешность составляет ,

3. Лист II. Динамические исследование основного механизма двухцилиндрового четырехтактного двигателя внутреннего сгорания.

3.2.1 Исходные данные и постановка задачи.

1	Средняя скорость поршня	(υВ)ср;(υВ’)ср	м/сек	10,26
2	Диаметр цилиндра	d	м	0,08
3	Отношение длины шатуна		-	4
4	Отношение расстояния от центра тяжести шатуна до точки А к длине шатуна		-	0,25
5	Число оборотов коленчатого вала двигателя при номинальной нагрузке		Об/мин	4400
6	Число оборотов коленчатого вала при холо­стом режиме		Об/мин	1600
7	Масса шатуна	m2, m4	кг	0,36
8	Масса поршня	m3,m5	кг	0,38
9	Момент инерции шатуна относительно оси, прохо­дящей через центр тяжести шатуна		кг*м2	0,002
10	Максимальное давление в цилиндре двига­теля при номинальной нагрузке	(pmax)ном	Па	28,8*105
11	Максимальное давление в цилиндре двига­теля при холостом режиме	(pmax)xx	Па	10,8*105
12	Коэффициент неравномерности вращения колен­чатого вала при холостом режиме	δ	-	1/25
13	Момент инерции коленчатого вала (без ма­ховика)		кг*м2	0,006
14	Угловая координата кривошипа для сило­вого рас­чета	φ1	град	30

Необходимо:

1. Провести геометрический синтез механизма.

2. Создать динамическую модель и определить момент полезного сопротивления на установившемся режиме.

3. Получить закон движения главного вала машины

4. Рассчитать маховик