
- •1. Техническое задание
- •1.1. Проектирование и исследование механизмов автомобиля повышенной проходимости
- •1.2. Исходные данные
- •2 Лист I. Проектирование зубчатой передачи и планетарного редуктора
- •2.1. Проектирование зубчатой передачи
- •2.1.1. Исходные данные и постановка задачи
- •2.1.3 Расчет зубчатой передачи
- •2.1.4. Построение проектируемой зубчатой передачи
- •2.1.5. Построение эвольвенты
- •2.1.6. Станочное зацепление
- •2.1.7. Графическое определение коэффициента перекрытия
- •2.1.8. Вывод
- •2.2 Проектирование планетарного редуктора
- •2.2.1. Исходные данные и постановка задачи
- •2.2.2. Основные условия проектирования многосателитного планетарного редуктора
- •2.2.3. Подбор чисел зубьев планетарного редуктора
- •2.2.4. Графическая проверка передаточного отношения
- •2.2.5. Выводы
- •3. Лист II. Динамические исследование основного механизма двухцилиндрового четырехтактного двигателя внутреннего сгорания.
- •3.2.1 Исходные данные и постановка задачи.
- •3.2.2 Геометрический синтез механизма.
- •3.2.3. Синтез механизма и результат
- •3.3. Динамическая модель, её параметры
- •3.3.1. Приведенный момент инерции
- •3.4. Определение передаточной функции
- •3.4.1. Построение плана скоростей
- •2.Определение передаточной функции
- •3.Определение передаточной функции
- •3.5.Построение суммарного приведенного движущего момента
- •Суммарного приведенного движущего момента
- •Приведенного момента инерции
- •3.7. Построение графика работы
- •Работа в зависимости от угла поворота φ
- •3.8. Расчет маховика
- •4 Лист 3 Проектирование кулачкового механизма
- •4.1 Исходные денные и постановка задачи
- •4.2 Построение кинематической диаграммы
- •4.3 Построение вспомогательной диаграммы
- •4.4 Проверка кинематических диаграмм
- •4.7 Вывод
- •Список литературы
2 Лист I. Проектирование зубчатой передачи и планетарного редуктора
2.1. Проектирование зубчатой передачи
2.1.1. Исходные данные и постановка задачи
Инструмент
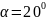 ,
m=8мм,
,
m=8мм,
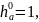


Колеса
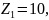

Необходимо:
Осуществить расчет эвольвентой зубчатой передачи;
Выбрать
коэффициент смещения
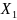 ,
при котором выполняются все условия
нормальной работы зубчатой передачи;
,
при котором выполняются все условия
нормальной работы зубчатой передачи;
Построить
зубчатую передачу и станочное зацепление
для колеса
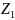 ;
;
Проверить графически коэффициент перекрытия;
2.1.2.
Выбор коэффициента смещения
TA \l "2.1.2.
Выбор коэффициента смещения
"
\s "2.1.2. Выбор коэффициента смещения
,𝑿-𝟏." \c 1

Расчетные
коэффициенты смешения производится с
использованием ЭВМ, по результатам
расчета строится блокирующий контур.
Коэффициенты смещения зубчатой передачи,
должны обеспечивать отсутствие подреза,
заклинивания, заострения зуба и
гарантировать минимально-доступную
величину коэффициента перекрытия.
Блокирующий контур представляет
собой совокупность кривых, построенных
в координатах
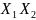 ,
ограничивающих выбор расчетных
коэффициентов смещения, и выделяющих
область допустимых значений.
,
ограничивающих выбор расчетных
коэффициентов смещения, и выделяющих
область допустимых значений.
Условия нормальной работы зубчатой передачи:
1.
Условие отсутствие подреза


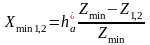 ,
где
,
где
 ;
;
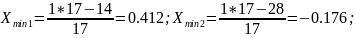
2.
Условие отсутствия заострения:
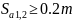 ;
;
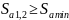
3.
Достаточность коэффициента перекрытия:
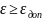
4.
Равномерный износ:

2.1.3 Расчет зубчатой передачи
В
связи со всем выше сказанным, рассмотрев
построенный блокирующий контур,
выбираем коэффициент смещения
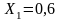 ,
при котором выполняются все условия
нормальной работы зубчатой передачи.
,
при котором выполняются все условия
нормальной работы зубчатой передачи.
Расчет
произведен для
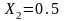 :
:
1. Угол зацепления



2. Коэффициент воспринимаемого смещения
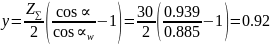
3. Коэффициент уравнительного смещения

4. Радиусы основных окружностей

 мм;
мм;
5. Радиусы начальных окружностей
 мм;
мм;
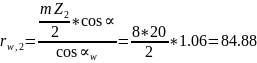 мм;
мм;
6. Межосевое расстояние
 мм;
мм;
Проверка
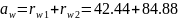 верно.
верно.
7. Радиусы основных окружностей
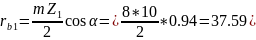 мм;
мм;
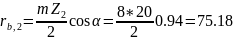 мм;
мм;
8. Радиусы окружностей вершин
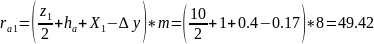 мм;
мм;
 мм;
мм;
9. Радиусы окружностей впадин
 мм;
мм;
 мм;
мм;
10. Высота зуба
 мм;
мм;
11. Проверка:
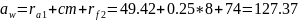 мм;
мм;
 мм;
Верно.
мм;
Верно.
12. Толщина зуба по дуге делительной окружности
 мм
мм
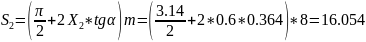 мм
мм
13. Толщина зуба по окружности вершин

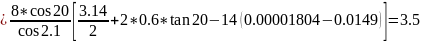 мм
мм
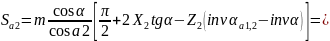
 мм
мм
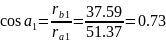 o
o
 o
o
14.
Проверка на отсутствие заострения зуба:
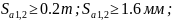 верно.
верно.
15. Коэффициент перекрытия для прямозубой передачи:
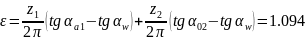
16. Достаточность полученного коэффициента перекрытия
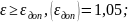 верно.
верно.
2.1.4. Построение проектируемой зубчатой передачи
По
вычисленным параметрам в выбранном
масштабе
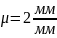 зубчатая передача строится следующим
образом:
зубчатая передача строится следующим
образом:
1. Откладывается межосевое расстояние аw
2.
Проводятся окружности начальные
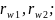 делительные r1,
r2
и
основные rb1,rb2;
окружности вершин ra1
ra2
и впадин rf1
rf2
делительные r1,
r2
и
основные rb1,rb2;
окружности вершин ra1
ra2
и впадин rf1
rf2
3. В точке касания начальных окружностей обозначаем полюс Р. Расстояние между делительными окружностями по осевой линии равно воспринимаемому смещению ym. Расстояние по осевой линии между окружностью вершин одного колеса и окружностью впадин другого колеса должно быть равно радиальному зазору с*m.
4.
Проводим линию зацепления касательную
к основным окружностям колес, через
полюс зацепления. Отмечаем предельные
точки линии зацепления N1
и N2
в
местах касания линии зацепления с
основными окружностями. Линия
зацепления образует с перпендикуляром,
восстановленном к осевой линии в полюсе,
угол зацепления
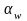 .
В1В2-
активная линия зацепления. Точка
пересечения окружности вершин второго
колеса с линией зацепления обозначается
В1-начало
линии зацепления, пересечение
окружности вершин первого колеса с
линией зацепления обозначается В2-
конец зацепления.
.
В1В2-
активная линия зацепления. Точка
пересечения окружности вершин второго
колеса с линией зацепления обозначается
В1-начало
линии зацепления, пересечение
окружности вершин первого колеса с
линией зацепления обозначается В2-
конец зацепления.
