7. Схема Горнера
Схема Горнера – это алгоритм деления многочлена на линейный множитель .
Пусть дан многочлен
.
Разделим многочлен
на линейный множитель
.
Для этого составим схему Горнера:
.
Таким образом,
,
где
.
Применения схемы Горнера
Деление многочлена на линейный множитель .
Пример.
Разделить многочлен
на (
)
.
Таким образом, получили
.
Нахождение значения многочлена в точке
:
(остаток от деления
на множитель (
)
даёт значение многочлена в этой точке).
Проверка, является ли корнем. Если , то – корень (в нашем случае
корнем не является) .
Нахождение кратности корня. Если в схеме Горнера два остатка равны нулю, а третий отличен от нуля, то кратность корня (как в данном случае) равна 2.
-
0
0
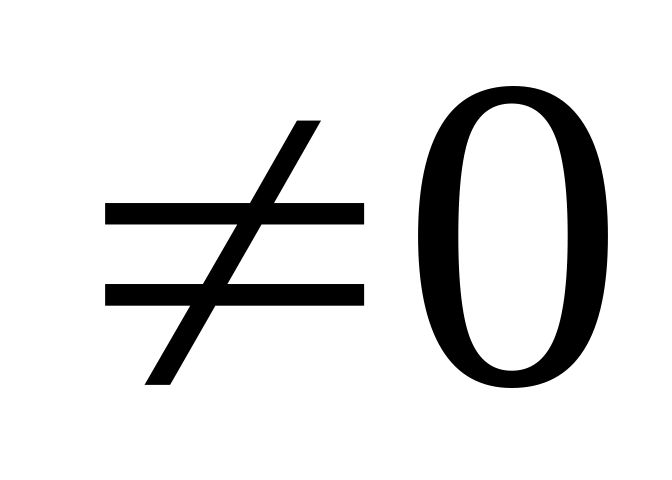
Разложение многочлена по степеням (
).
Пусть дан многочлен
.
Разложим его в ряд Тейлора:
.
Заметим, что
,
,
…………………………………………….
,
для всех значений
,
поэтому
и, следовательно, справедлива следующая
формула:
.
Разделим многочлен на линейный множитель :
-
(…)
[…]
Нахождение производных многочлена в точке (
):
-
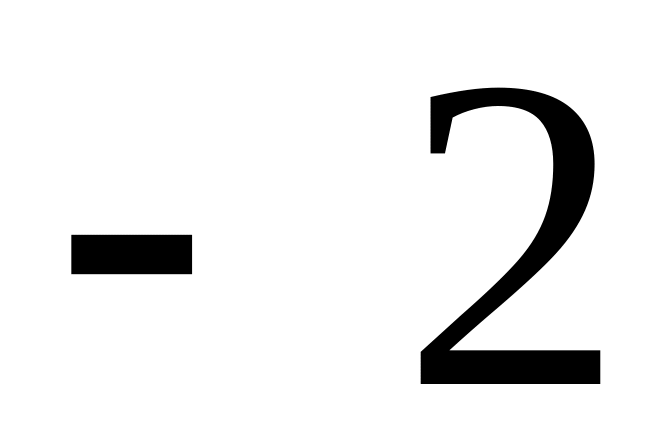1
0
2
7
–2
1
–2
6
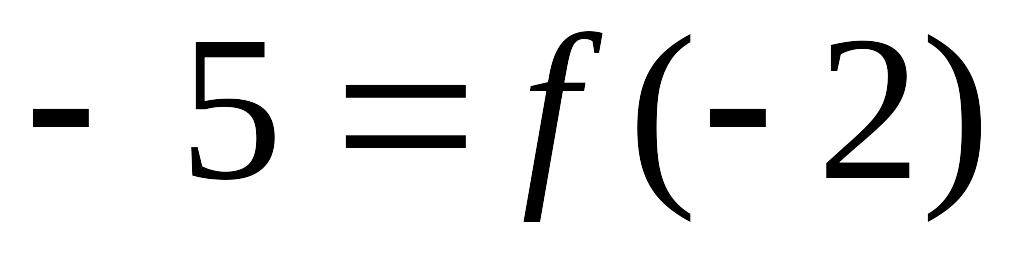
–2
1
–4
–2
1
–2
Таким образом,
,
,
.
8. Отделение кратных корней многочлена
Теорема.
Корень кратности
многочлена
является корнем кратности
его производной
.
Следствие. Простой корень многочлена (т.е. корень кратности один) не является корнем его производной.
Пусть дан многочлен .
Отделением
кратных корней
для многочлена
называется построение такого многочлена
,
который имеет те же корни, что и
,
но не имеет кратных корней:
.
№ 585 [1]. Отделить кратные множители полиномов:
a)
.
1. Вычислим
производную:
.
2. Найдем
:
;
.
Так как
,
то
.
3. Отделим кратные корни многочлена:
.
Следовательно,
.
4. Определим
кратность корней
и
.
Для этого воспользуемся схемой Горнера
(см. п. 7).
-
1
0
– 6
–4
9
12
4
2
1
2
–2
–8
–7
–2
0
2
1
4
6
4
1
0
2
1
6
18
40
81
0–1
1
3
3
1
0
–1
1
2
1
0
–1
1
1
0
–1
1
0
Очевидно, что – корень кратности 2, а – корень кратности 4.