27

,

где – матрица перехода от базиса к базису .

Таким образом, матрица оператора простой структуры подобна диагональной матрице. Очевидно, что справедливо и обратное

Утверждение. Любая матрица, подобная диагональной, является матрицей некоторого оператора простой структуры.

Поэтому, если оператор имеет в некотором базисе матрицу , то в базисе из собственных векторов он имеет матрицу , где – матрица перехода от базиса к базису из собственных векторов .

Замечание. Легко показать, что .

Определение. Каноническим базисом в пространстве называется совокупность векторов .

Пример. Пусть .

Собственные векторы матрицы , , , а соответствующие им собственные значения , , . Матрица оператора в базисе из собственных векторов имеет вид

.

Матрица перехода от канонического базиса пространства к базису из собственных векторов имеет вид

.

Приведем один достаточный признак оператора простой структуры.

Теорема. Если все корни характеристического многочлена матрицы оператора различны, то оператор имеет простую структуру.

Д о к а з а т е л ь с т в о

следует из того, что в этом случае оператор имеет попарно различных собственных чисел и, следовательно, линейно независимых векторов.

Действие оператора простой структуры можно описать следующим образом. В пространстве имеется таких “направлений”, что каждый из линейно независимых векторов, имеющих одно из этих “направлений”, преобразуется оператором в вектор, ему коллинеарный. Произвольный вектор преобразуется по формуле

.

Найдем теперь необходимые и достаточные условия, при которых оператор имеет простую структуру.

Теорема. Для того чтобы оператор имел простую структуру, необходимо и достаточно, чтобы для каждого корня характеристического уравнения кратности ранг матрицы был равен .

Д о к а з а т е л ь с т в о.

Необходимость. Если оператор имеет простую структуру, то

.

Тогда

.

Значит, матрицы и подобны и имеют один и тот же ранг. Ранг матрицы равен числу диагональных элементов, отличных от нуля, или числу корней характеристического уравнения, не равных , то есть равен .

Достаточность. Пусть – попарно различные собственные значения оператора . Собственные векторы с собственным значением образуют подпространство размерности пространства . Так как по условию , то оператор имеет линейно независимых собственных векторов с собственным значением . Таким образом, мы имеем собственных векторов . Покажем, что они линейно независимы. Пусть

( – нулевой вектор) и, например, .

Введем в рассмотрение оператор

и рассмотрим оператор

.

Имеем

.

Тогда , , что противоречит линейной независимости собственных векторов, соответствующих собственному значению .

Опишем способ построения собственных векторов оператора .

Координаты собственных векторов в некотором базисе можно найти, решая системы уравнений

,

где – попарно различные собственные значения оператора. В найденном базисе из собственных векторов оператор имеет диагональную матрицу. Предлагаемый новый способ построения базиса из собственных векторов состоит в нахождении подпространства пространства , целиком состоящего из собственных векторов оператора, соответствующего собственному значению . Этот способ далее будет применен к построению жорданова базиса. Рассмотрим подпространство , размерность которого

.

Так как оператор имеет простую структуру, то , и в подпространстве оператор не имеет собственных векторов, отвечающих собственному значению . Аналогично подпространство

имеет размерность и не содержит собственных векторов с собственными значениями , а значит, оно состоит из собственных векторов оператора , отвечающих собственному значению . Действительно, так как , то в этом подпространстве можно выбрать базис только из собственных векторов, отвечающих и, следовательно, любой ненулевой вектор этого подпространства – собственный.

Таким образом, с помощью операторов можно представить пространство в виде суммы подпространств , размерности которых равны соответственно. Каждое из этих подпространств состоит только из собственных векторов оператора , отвечающих одному собственному значению. Выбирая базис в каждом подпространстве , мы получили базис во всем пространстве . Поэтому для отыскания всех независимых собственных векторов оператора простой структуры, отвечающих собственному значению , достаточно построить любой базис пространства . Для этого выберем произвольный базис пространства , составленный из векторов , координаты которых относительно исходного базиса соответственно равны

,

,

…………………….

.

Найдем образы векторов в подпространстве : . Среди них всегда найдется линейно независимых векторов, которые и примем за базис в . Каждый из векторов является -м столбцом матрицы , а матрица состоит из векторов , поставленных в столбцы. Так как матрица – произвольная невырожденная матрица, то можно считать, что или . В этом случае матрица . Это означает, что в качестве базиса подпространства можно выбрать любые линейно независимых столбцов матрицы .

Из приведенных рассуждений следует

Теорема. Для того чтобы оператор имел простую структуру, необходимо и достаточно, чтобы

.

Д о к а з а т е л ь с т в о.

Необходимость. Подпространство состоит только из собственных векторов оператора , отвечающих собственному значению , а поэтому оператор аннулирует это пространство, то есть

.

Достаточность. Из соотношения следует, что состоит только из собственных векторов оператора, отвечающих . Размерность этого подпространства равна геометрической кратности корня , так как операторы , входящие в , не могут изменить кратности корня . Строя базис в каждом подпространстве , мы получим базис всего пространства.

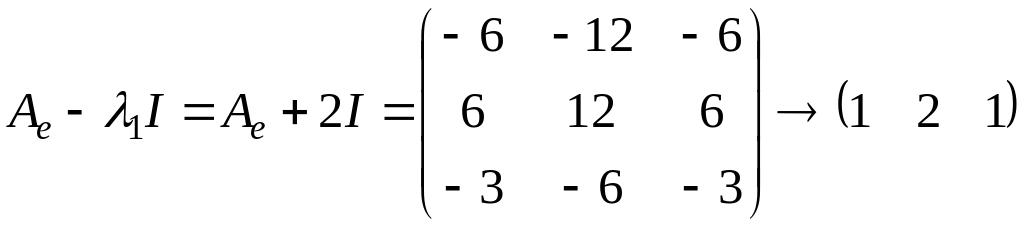Пример. Пусть матрица оператора имеет вид . Характеристическое уравнение имеет корни , . Рассмотрим кратный корень . Матрица имеет ранг . Так как , то и, следовательно, оператор – оператор простой структуры. Рассмотрим матрицы и . Первая матрица имеет ранг 1, векторы , – линейно независимы и являются собственными векторами для . Вторая имеет один линейно независимый столбец, поэтому в качестве собственного вектора для собственного значения возьмем вектор .

Найдем теперь необходимые и достаточные условия, при выполнении которых оператор не является оператором простой структуры.

Теорема. Чтобы оператор не имел простой структуры, необходимо и достаточно, чтобы существовали вектор и собственный вектор с собственным значением , удовлетворяющие условию

.

Д о к а з а т е л ь с т в о.

Необходимость. Пусть , то есть образ подпространства содержит ненулевые векторы. Тогда в подпространстве найдется хотя бы один собственный вектор оператора . Обозначим через вектор подпространства , перешедший в под действием оператора . Очевидно, что

.

Достаточность. Пусть , тогда и . Поэтому .