3.4. Цепи Маркова

Обобщением схемы независимых испытаний является схема цепей Маркова. Пусть производится последовательность испытаний, в каждом из которых может осуществиться одно и только одно из n несовместных событий (верхний индекс означает номер испытания).

Говорят, что такая последовательность образует цепь Маркова, если вероятность того, что в (k + 1)-м испытании (k = 1, 2, …) наступит событие , зависит только от того, каким было событие при k-м испытании, и не зависит от исходов всех предыдущих испытаний.

События называются состояниями цепи Маркова или состояниями некоторой системы. Цепь Маркова ограничена, если число состояний системы конечно. Система изначально может находиться в состоянии с вероятностью a_i. Вектор а = а_1, а_2, … , а_n называется вектором начальных вероятностей.

Цепь Маркова называется однородной, если условная вероятность события при условии, что в k-м испытании произошло событие , не зависит от номера испытания k , а зависит только от номера события. Такая вероятность называется вероятностью перехода из i-го состояния в состояние j и обозначается Совокупность вероятностей образует матрицу перехода

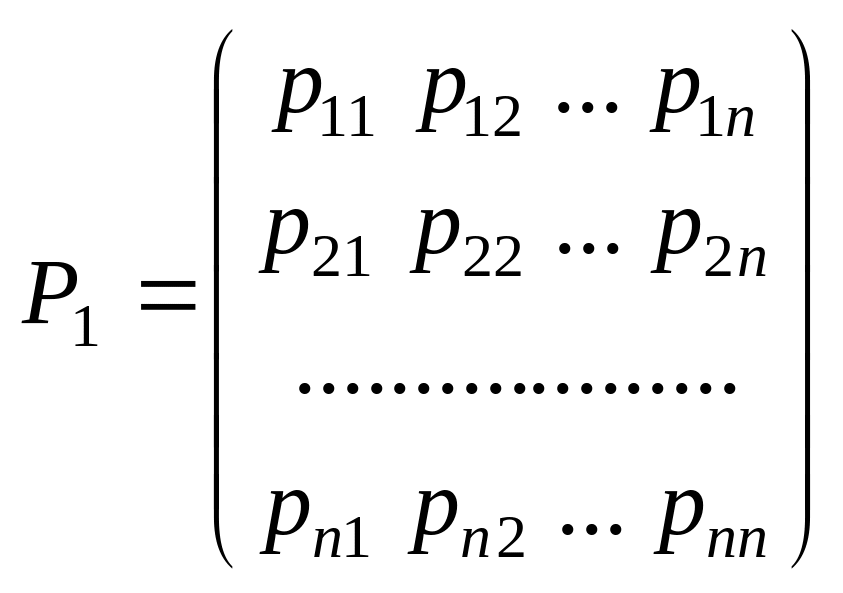, (3.9) где т.е. сумма вероятностей каждой строки матрицы перехода равна единице.

Вероятности перехода через m испытаний составят матрицу

(3.10)

Свойства однородных марковских цепей полностью определяются вектором начальных вероятностей и матрицей перехода. В некоторых случаях для наглядности используется граф, вершинами которого являются состояния системы, а рядом со стрелкой, соединяющей состояние А_i c состоянием A_j, указывается соответствующая вероятность перехода p_ij. Если p_ij = 0, стрелка не проводится.

3.35. Даны вектор начальных вероятностей а = 0,25, 0,5, 0,25 и матрица вероятностей перехода за один шаг:

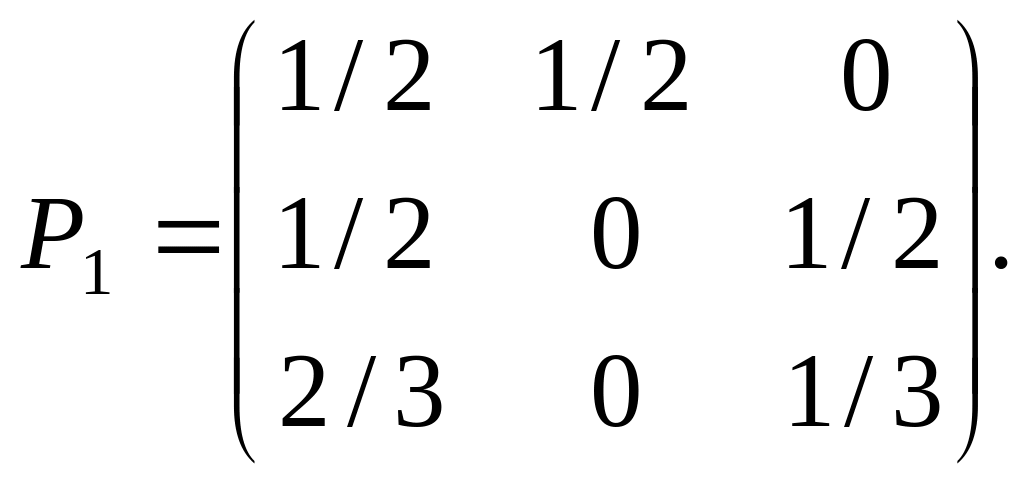
Требуется: 1) построить граф, соответствующий матрице Р₁; 2) построить граф состояний системы через два шага, если известно, что система вначале находилась в состоянии А₃; 3) найти вероятность того, что через три шага система будет в состоянии А₁.

 1. Граф, соответствующий матрице перехода Р₁:

2. Граф возможных состояний системы через два шага при условии, что система находилась в состоянии А₃:

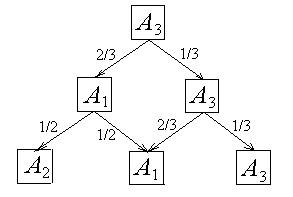
3. Пусть Н₁, Н₂, Н₃ – гипотезы о том, что система вначале находится в состоянии А₁, А₂, А₃ соответственно, а случайное событие состоит в том, что система через три шага находится в состоянии А₁. По условию Найдем матрицу вероятностей перехода через три шага.

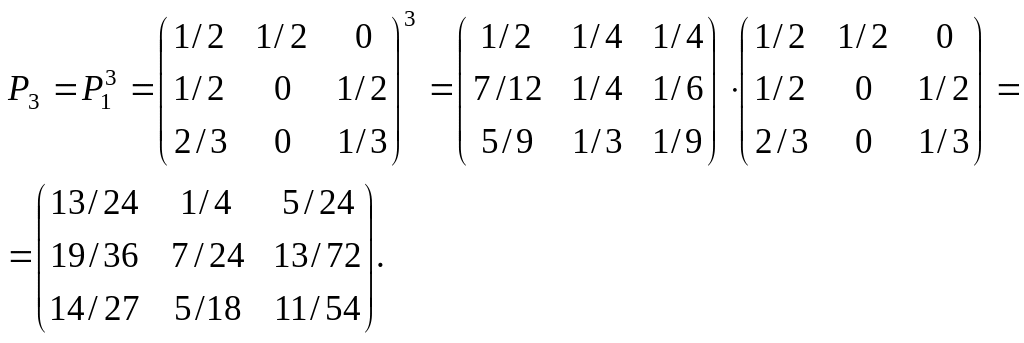
Отсюда находим условные вероятности Тогда по формуле полной вероятности



В задачах 3.36 – 3.39 найти матрицы перехода из состояния в состояние за 2 шага.

3.36. 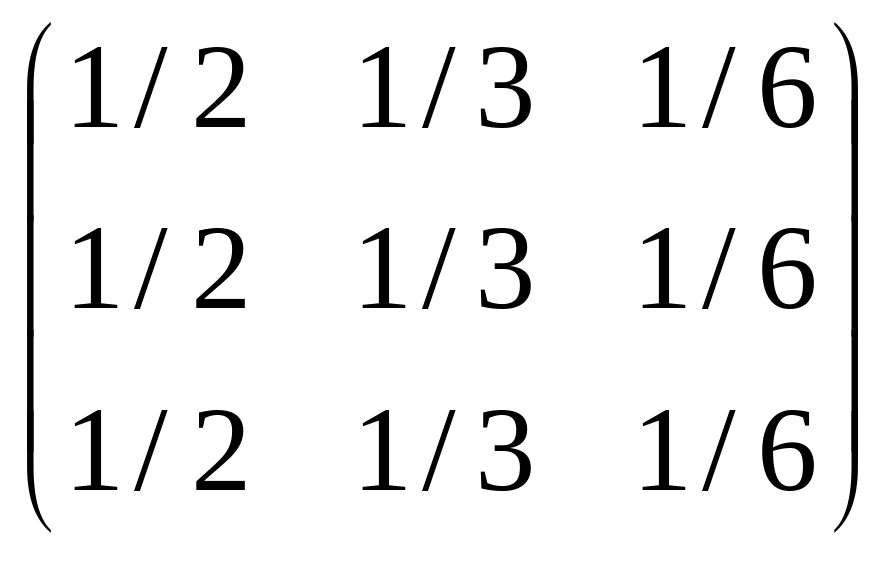. 3.37.

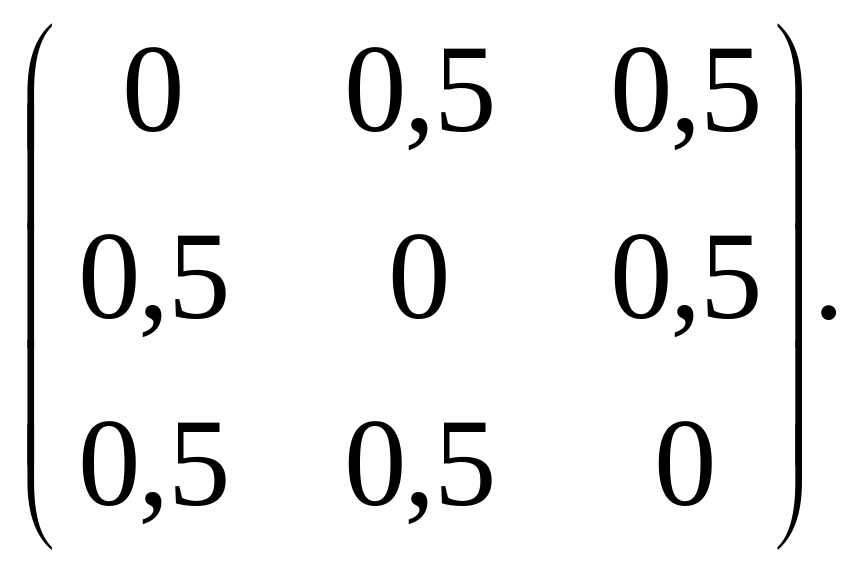
3.38. 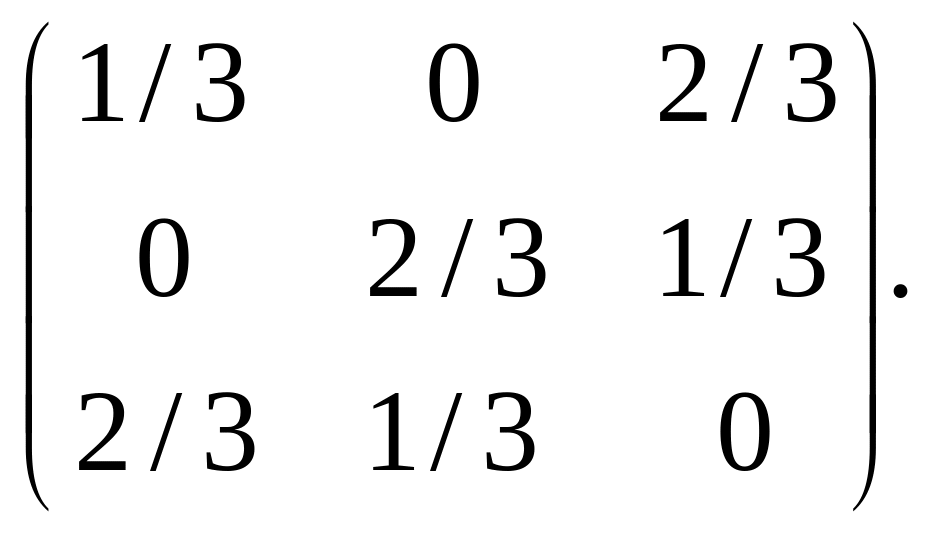3.39.

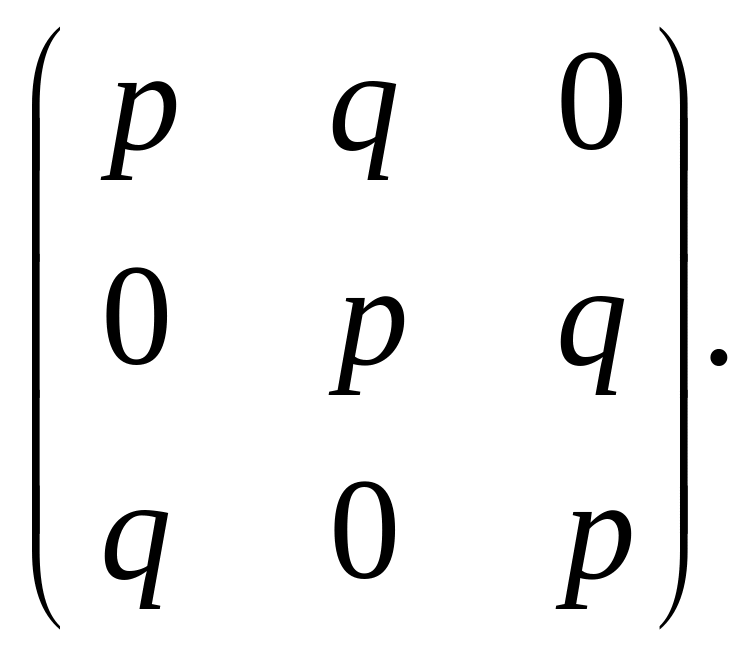
В задачах 3.40 – 3.41 найти матрицы перехода из состояния в состояние за 3 шага.

3.40. 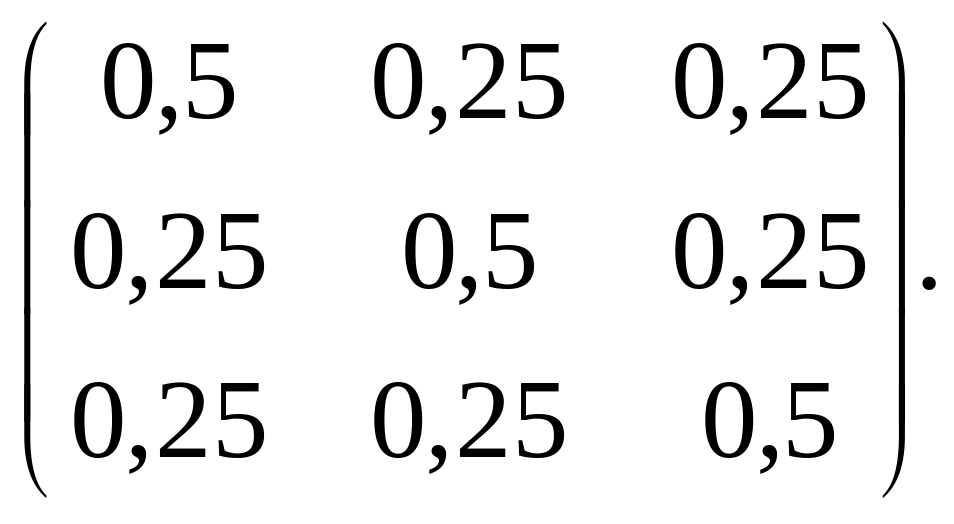3.41.

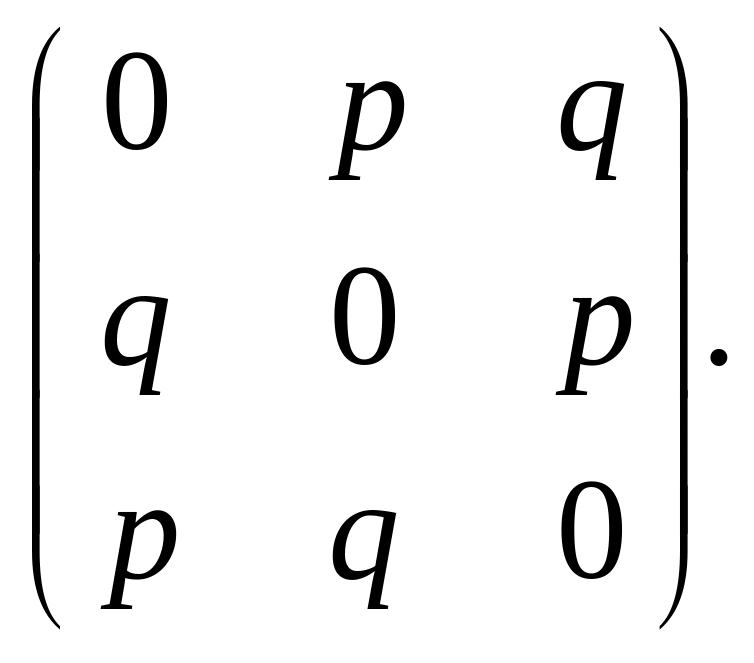
3.42. На окружности расположены шесть точек А₁, …, А₆, равноотстоящих друг от друга. Частица движется из точки в точку следующим образом. Из данной точки она перемещается в одну из ближайших соседних точек с вероятностью 0,25 или в диаметрально противоположную точку с вероятностью 0,5. Выписать матрицу вероятностей перехода для одного шага и построить граф, соответствующий этой матрице.

3.43. Вероятности перехода за один шаг в цепи Маркова заданы матрицей

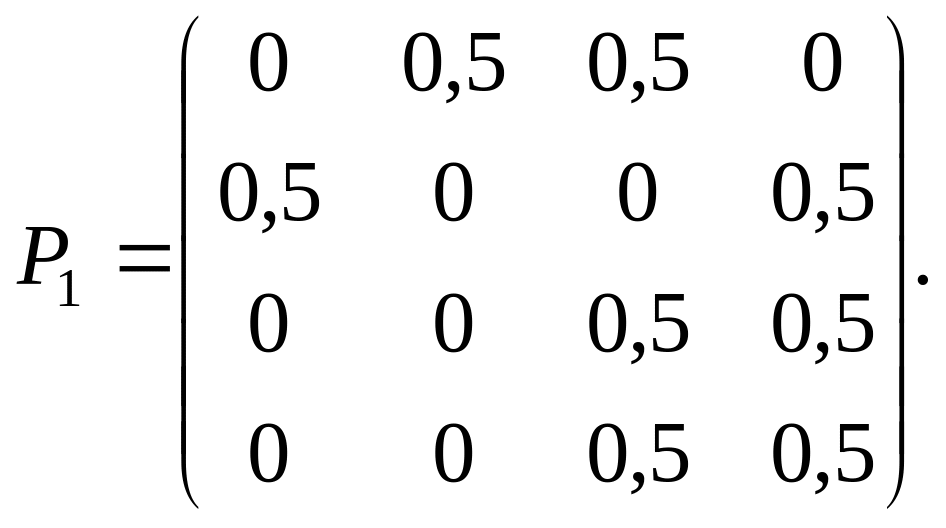
Требуется найти число состояний и построить граф, соответствующий этой матрице.

3.44. Имеются две монеты: одна – правильная, а у другой вероятность выпадения герба равна 2/3. Если в предыдущий раз выпал герб, то подбрасывают правильную монету; в противном случае бросается вторая монета. Пусть в первый раз выпала цифра. Постройте граф возможных состояний после трех последовательных бросаний монеты. Какова вероятность того, что по крайней мере два раза выпадет герб? Составьте для этого процесса матрицу вероятностей перехода.

3.45. В учениях участвуют два корабля, которые одновременно производят выстрелы друг в друга через равные промежутки времени. При каждом обмене выстрелами корабль А поражает корабль В с вероятностью 0,5, а корабль В поражает корабль А с вероятностью 0,375. Предполагается, что при любом попадании корабль выходит из строя. Рассматриваются результаты серии выстрелов. Найти матрицу вероятностей перехода, если состояниями цепи являются комбинации кораблей, оставшихся в строю: А₁ – оба корабля в стою, А₂ – в строю корабль А, А₃ – в строю корабль В, А₄ – оба корабля поражены.

3.46. Рассмотрим марковскую цепь с двумя состояниями А₁ и А₂ и матрицей вероятностей перехода

С помощью особого устройства случайного выбора мы выбираем состояние, с которого начинается процесс. Это устройство выбирает А₁ с вероятностью 0,5 и А₂ с вероятностью 0,5. Требуется: а) найти вероятность того, что после первого шага этот процесс перейдет в состояние А₁;

б) то же самое для случая, когда это устройство выбирает А₁ с вероятностью 1/3 и А₂ с вероятностью 2/3.

3.47. Погода на некотором острове через длительные периоды становится то дождливой (А₁), то сухой (А₂). Вероятности ежедневных изменений заданы матрицей

а) Если в среду погода дождливая, то какова вероятность, что она будет дождливой в ближайшую пятницу?

б) Если в среду ожидается дождливая погода с вероятностью 0,3, то какова вероятность, что она будет дождливой в ближайшую пятницу?

3.48. В некоторой местности погода весьма изменчива. Здесь никогда не бывает двух ясных дней подряд. Если сегодня ясно (Я), то завтра с одинаковой вероятностью пойдет дождь (Д) или снег (С). Если сегодня снег (или дождь), то с вероятностью 0,5 погода не изменится. Если все же она изменится, то в половине случаев снег заменяется дождем или наоборот, и лишь в половине случаев на следующий день будет ясная погода. Требуется:

а) принимая в качестве состояний цепи различные виды погоды Я, Д, С, составить матрицу вероятностей перехода;

б) построить граф, соответствующий матрице перехода;

с) определить вероятность ясной погоды через три дня после дождя.

37