Контрольные вопросы

1. Что такое кажущиеся и истинные числа переноса?

2. Какие способы установления чисел переноса вы знаете?

3. Какие факторы влияют на числа переноса?

4. Напишите уравнение связи чисел переноса ионов с их подвижностями?

Работа 2 определение константы диссоциации слабого электролита

Способность раствора проводить электрический ток обусловлена движением ионов, которые образуются вследствие электрической диссоциации вещества. Для характеристики электропроводности электролита используют величины удельной χ и мольной λ электропроводности, которые могут быть представлены выражениями:

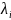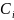χ= 1/ ρ; ∑ = χ/∑ , (2.1)

где ρ – удельное сопротивление, Ом*м;

χ – удельная электропроводность, Ом^-1*м^-1;

с – концентрация, моль/л;

λ – ионная электропроводность, Ом^-1*м²*моль^-1.

Удельная электропроводность численно равна току (А), проходящему через слой раствора с поперечным сечением 1м² и протяженностью 1 м под действием градиента потенциала 1 В/м.

На практике во многих случаях удобнее пользоваться мольной электропроводностью, которая равна проводимости 1м³ раствора, содержащего 1 моль электролита.

Мольная проводимость зависит от концентрации раствора. С уменьшением концентрации она увеличивается и достигает предельного значения, которое называется электропроводностью при бесконечном разбавлении и обозначается 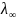или .

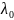Для слабых электролитов зависимость электропроводности от концентрации раствора определяется изменением степени диссоциации

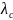= α_сЧλ₀, (2.2)

где α_с – степень диссоциации при концентрации электролита С;

λ_с – мольная электропроводность при концентрации электролита равной С.

Мольная электропроводность может быть выражена и через подвижности ионов

λ_с = α_сЧ (v₊+v_-), (2.3)

где v₊ и v_- - подвижности катиона и аниона соответственно; м²/моль*Ом.

Подвижности ионов определяются произведением их абсолютной скорости движения на постоянную Фарадея:

v₊ = v⁰ + ЧF; v_-= v⁰ – ЧF. (2.4)

мольная электропроводность сильных электролитов до концентраций не выше 0,02 М описывается уравнением Кольрауша, которое позднее теоретически было обосновано Онзагером:

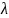_с = λ₀ - α√с. (2.5)

Постоянная α зависит от природы растворителя, температуры и валентного типа электролита. Эквивалентная электропроводность сильного электролита может быть выражена через подвижности ионов

λ_с = 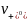+ 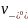. (2.6)

Измерение электропроводности растворов слабых электролитов дает возможность определить константу электролитической диссоциации, связанную со степенью диссоциации уравнением

K_d = 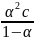. (2.7)

Подставив значения степени диссоциации α_с = λ_с/λ₀ в уравнение (2.7), найдем

K_d = 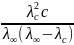. (2.8)

Решив уравнение (2.8) относительно произведения λ_с*с, после некоторых преобразований получим:

λ_с *с = K_d 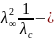K_{d ,} (2.9)

то есть произведение λ_с *с представляет линейную функцию от 1/ :

λ_с *с = α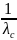 + b, (2.10)

где α = K_{d *} ,

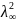b = K_{d *}

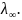
Для слабых электролитов, степень диссоциации которых незначительна, уравнение (2.7) может быть преобразовано, если пренебречь величиной α_с в знаменателе, малой в сравнении с единицей:

K_d ≈α²*с, (2.11)

заменив теперь степень диссоциации отношением электропроводностей, получим:

K_d = 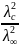*с. (2.12)

После логарифмирования уравнения (2.12) примет вид:

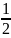lg λ_c = lg λ_∞√K_d - lg c. (2.13)

Если величина λ₀ , то, строя график в координатах lg λ_с – lg c, можно рассчитать K_d слабого электролита.