Некоторые приложения в экономике собственных чисел и собственных векторов матрицы.

1. Линейные модели обмена.

Пусть имеется система из n отраслей производства, каждая из которых выпускает продукцию одного вида.

Примем за единицу объёма продукции каждой отрасли в рассматриваемом периоде. Обмен продукции происходит только внутри системы (экономика замкнута) и известна матрица А:

,

где а - доля продукции j-й отрасли, которая поступает в i-ю отрасль.

Ясно, что для матрицы А выполнимы два условия:

1. , для j= ; 2. а , для i = , j= .

Первое условие вызвано тем, что вся продукция j-й отрасли предназначена для обмена внутри системы.

Матрица, для которой выполнимы условие 1 и 2, называется матрицей обмена.

Требуется установить такие цены на продукцию каждой отрасли, при которых вся система находится в равновесии, то есть ни одна отрасль не обогащается за счет другой.

Пусть х_i – цена одной единицы продукции i-й отрасли, а - вектор цен. Тогда расход i-й отрасли, то есть стоимость всей закупаемой ею продукции, таков: .

Чтобы отрасль могла развиваться, её расход не должен превышать дохода, который равен стоимости произведённой ею продукции, то есть х_i.

, i = (1)

Если искомые равновесные цены существуют, то система неравенств выполняется для них как система равенств.

Доказательство.

Пусть числа удовлетворяют условию (1), подставим их в эти неравенства и сложим почленно все полученные неравенства

; ; ,

но это неравенство является равенством и все слагаемые в сумме неотрицательны, то и исходные неравенства (1) выполняются для чисел . Как равенства: .

Итак, надо найти вектор такой, что

Таким образом, задача свелась к следующему:

1. Является ли число =1 собственным числом матрицы обмена А.

2. Если да, то найти соответствующий ему положительный собственный вектор матрицы А.

Для того, чтобы было собственным числом матрицы обмена, необходимо и достаточно, чтобы выполнялось равенство , т.е.

.

Элементы первой строки равны 0, т.к. в матрице обмена в силу этого определитель, содержащий нулевой ряд, равен 0.

Итак, число 1 собственное число матрицы обмена, для отыскания соответствующего ему собственного вектора , следует найти полуположительное решение однородной системы.

Такое решение существует и найденный полуположительный вектор , является искомым вектором равновесных цен.

Задача. Экономическая система состоит из 3-х отраслей производства, каждая из которых выпускает один вид продукции. Обмен внутри системы происходит в соответствии с данной матрицей обмена 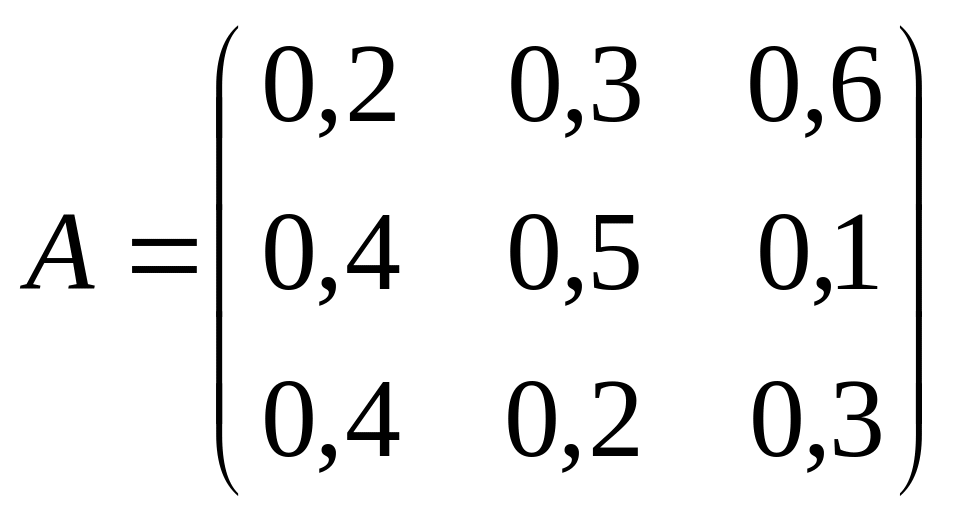. Найти вектор равновесных цен.

Решение.

Сначала найдём матрицу : .

Составим однородную систему линейных уравнений , где .

;

эта система равносильна системе уравнений

находим её общее решение: . Принимая , получим .

Таким образом, равновесные цены на продукцию каждой отрасли: , где к можно трактовать как множитель, связанный с денежной единицей.

2. Модель международной торговли

Рассмотрим систему из N стран, торгующих только друг с другом (т.е. система замкнута). Известна матрица , где – доля средств j – ой страны, затрачиваемая на импорт из i – ой страны . Матрица А является матрицей обмена, т.е. и ( ). Требуется найти первоначальное распределение средств между странами, обеспечивающие равновесие всей системы, т.е. такое положение, при котором в каждой стране после каждого цикла обмена остается столько же средств, сколько было до обмена.

Пусть Х_i – количество средств i – ой страны, т.е. вектор описывает искомое распределение средств. Ясно, что надо найти вектор , удовлетворяющий условиям: .

Число 1 есть собственное число матрицы обмена А и существует полуположительный собственный вектор матрицы А, соответствующий этому числу. Вектор и является искомым первоначальным распределением средств.

Система при этом будет находиться в равновесии, т.е. расход каждой страны в каждом цикле обмена совпадает с её доходом от экспорта и не изменяется от цикла к циклу.

Проанализируем структуру равновесных векторов на модели.

Международная модель 6 стран описывается матрицей обмена

I II III IY Y YI

Найти равновесный вектор этой системы.