Исследования плоского электростатического поля

Цель работы: 1. Закрепление знания характеристик электростатического поля, получение навыка их измерения и расчета, построение картины электростатического поля.

Приборы и принадлежности: вольтметр, генератор, электролитическая ванна с координатной сеткой.

Теория вопроса

Напряженность электростатического поля численно равна силе, которая действует на единичный положительный заряд в данной точке поля. Направление вектора совпадает с направлением действия силы:

. ( 1 )

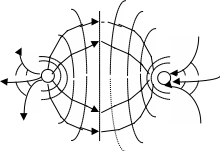
При графическом изображении поля проводят линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности . Эти линии называют силовыми линиями электростатического поля (рис. 1).

+  _ + +

а б

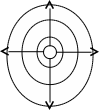
Р и с. 1. Силовые и эквипотенциальные (пунктирные) линии электрического поля двух противоположно заряженных точечных зарядов (а) и положительного точечного заряда (б).

Энергетической характеристикой поля является потенциал. Потенциал поля в данной точке определяют как работу, которую необходимо произвести, перемещая единичный положительный заряд из бесконечности в данную точку, или как величину потенциальной энергии электрического поля, отнесенную к величине заряда, помещенного в данную точку. Потенциал электростатического поля, созданного точечным зарядом q, в точке, которая находится на расстоянии r от заряда, выражается формулой:

. (2)

Геометрическое место точек электрического поля, потенциалы которых равны, называют эквипотенциальной поверхностью или эквипотенциальной линией (в случае двух измерений). В соответствии с (рис.1,б) эквипотенциальная поверхность точечного заряда - сферическая, а эквипотенциальная линия – окружность.

Можно доказать, что силовые линии ортогональны эквипотенциальным поверхностям (рис.1). Действительно, работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю (т.к. dφ =0). С другой стороны, dA = F_edl = 0, т.е. F_e = 0. Это возможно тогда, когда ), т.е. . Следовательно, силовые линии всегда направлены по нормали к эквипотенциальным поверхностям. Чтобы судить о величине напряженности электрического поля эквипотенциальные поверхности проводят так, чтобы разность потенциалов между соседними поверхностями была равна 1 В.

Между обеими величинами, характеризующими электростатическое поле, т.е. между напряженностью электростатического поля и потенциалом имеется следующая зависимость:

(3)

где dl - элементарный отрезок, а d - падение потенциала на этом отрезке, E_l – проекция вектора на отрезок dl. Эту зависимость можно записать в векторной форме:

, (4)

где градиент потенциала ;

- оператор Набла .

В малом объеме между двумя эквипотенциальными линиями электростатическое поле (рис. 2) приближенно можно считать однородным .