§5. Несобственные интегралы
В определении определенного интеграла предполагается, что подынтегральная функция f(x) ограниченна на [a; b], и промежуток [a; b] конечен. В данном пункте вводятся несобственные интегралы, для которых ограничение конечности промежутка снимается.
Определение 4. Несобственными интегралами с бесконечными пределами интегрирования называются интегралы, определяемые следующим образом:
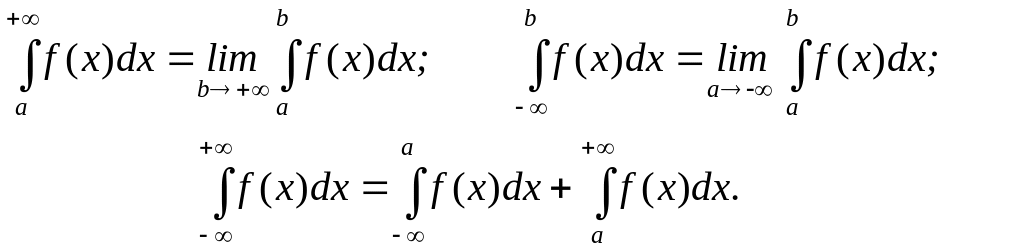
В
торой
вид несобственных интегралов – это
интегралы от неограниченных функций.
Пусть функция f(x)
непрерывна на [a; b]
кроме точки с[a;
b], в которой f(x)
имеет разрыв II рода.
Тогда несобственный интеграл интеграл
от f(x)
в пределах от а до b
определяется, как сумма следующих
пределов:
Если при вычислении несобственного интеграла получаемый предел конечен, то говорят, что несобственный интеграл сходится, если нет, то расходится.
Пример 14. Вычислить следующие несобственные интегралы.
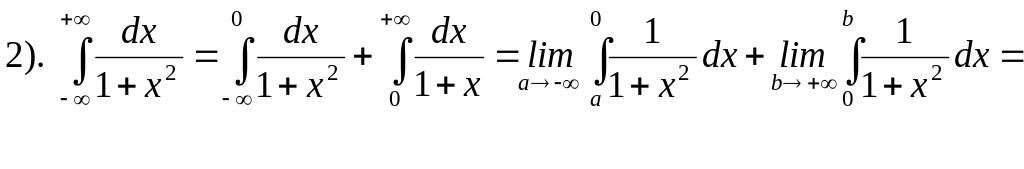
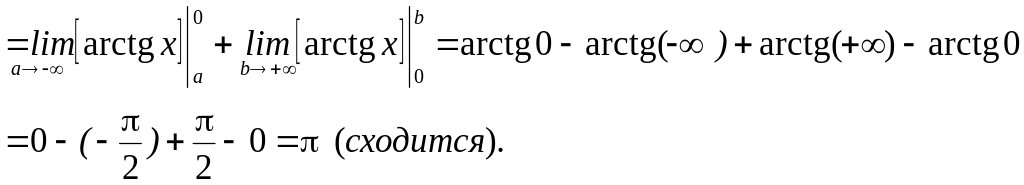
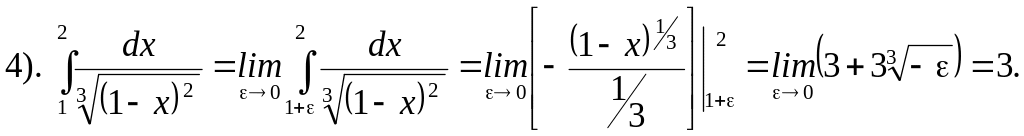
И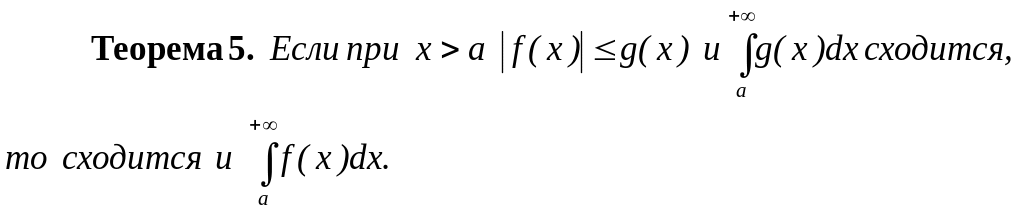
ногда
не требуется вычислять данный несобственный
интеграл, а достаточно только выяснить
его сходимость. В таких случаях часто
сходимость несобственного интеграла
устанавливается методом сравнения,
который опирается на следующее
утверждение.
Упражнения
Найти следующие интегралы.
1). (x4 3x3 + 2x)dx. 2). (x 3x2)(2 – x)dx. 3). (2x 3x1/2 + 4x1/3 – 5/x)dx.
4).
5).
6).
10). (3 2х)4 dx. 11). (ех + ех)2dx. 12). (14х) dx.
1
6).
х
ln(x
1)
dх.
17). хех
dх.
18). х
lnx
dx.
1
.Вычислить
определенные интегралы:
2. Вычислить площадь, ограниченную линиями:
1). y = 0 и y = 9 – x2. 2). y = 0 и y = 3 – 2x – x2.
3). y = x2 и y = 2 – x2. 4). xy = 6 и x + y = 7.
5). x = 0 и y2 = 2x + 4. 6). y2 = x3, y = 8, x = 0.
7). y = 2x , y = 2, x = 0. 8). y = ex, y = ex, x = 1.
3.Определить объем тела, образованного вращением вокруг оси Ох или Оу фигуры, ограниченной указанными линиями:
1). y2 = 4x, x = 5 вокруг Ох. 2). хy = 4, x = 1, x = 4, у = 0 вокруг Ох.
3). y2 = 4 x, x = 0 вокруг Оy. 4). y = x3, x = 0, у = 8 вокруг Оy.
4
.
Вычислить несобственные интегралы: