Свойства интегралов

1). Производная от интеграла по переменной интегрирования равна подынтегральной функции: ( f(x)dx) = f(x).

2). Интеграл от дифференциала функции равен самой функции:

 du = u +c.

3). Если функции f(x) и g(x) интегрируемы, то сумма этих функций

интегрируема, и верно равенство:

4). Если функция f(x) интегрируема, то для любого числа с произведение cf(x) интегрируемо и верно равенство:

 cf(x)dx = c f(x)dx.

Доказательство. Согласно равенствам (48) и (49), ( f(x)dx) = (F(x) + c) = f(x), следовательно, свойство 1) доказано. Аналогично доказывается свойство 2). Далее, в силу свойств производной и свойства 1),

( ) = = .

Следовательно, свойство 3) доказано. Аналогично доказывается свойство 4).

В следующих примерах подынтегральная функция преобразовывается в сумму табличных интегралов и затем применяются свойства 3), 4). Этот метод называется методом разложения. Для краткости исходные инте­гралы обозначаются символом  .

Пример 3. Найти следующие интегралы.

1).  (x³  3x² + 2x – )dx.

По указанным выше свойствам и формулам 1, 2 таблицы интегралов,  =  x³ dx  3 x² dx + 2 x dx – 4 dx = 0,25х⁴  х³ + х² – 4ln |x| + c.

2).  (x² – 2)²dx.

Раскрываются скобки и, по формуле 1, получается:  = (x⁴  4x² + 4)dx = x⁵  x³ + 4x + c.

П рименяются вспомогательные формулы а), б) из пункта 1 таблицы интегралов:

К 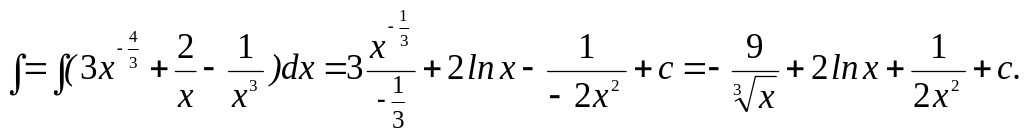аждое слагаемое в скобках умножается на , получен­ные выражения интегрируются, как в предыдущих примерах:

П рименяется формула 4:

В более полных курсах по математике доказывается следующее ут­верждение.

Теорема 1. Если функция f(x) непрерывна или имеет только конечное число конечных разрывов на некотором интервале, то она интегрируема в этом интервале.

Согласно теореме 1 из §4 главы 4, всякая элементарная функция непрерывна там, где она определена. Поэтому она имеет первообразную в своей области определения. Но не всегда эта первообразная является элементарной функцией. Например, следующие интегралы от элементарных функций существуют, но не являются элементарными функциями:

Такие интегралы называются неберущимися, они вычисляются с помощью специальных методов, которые в данном курсе не рассматриваются. Здесь изучаются только некоторые методы интегрирования, которые дают элементарные функции.

§2. Методы интегрирования

1. Метод введения нового аргумента. Если , то . Более того, если функция u = (x)- непрерывно диффе­ренцируемая функция, то , и в таких случаях допускается запись вида:

Пример 4. Найти интегралы.

1). (1 + х)⁴ dx.

Ясно, что dx = d(x +1), поэтому пусть u = (x +1), тогда

 = (1 + х)⁴ d(х +1) =  u⁴ du = + с = + с.

2).  2х(х² +1)³ dx.

Здесь d(x² +1) = 2xdx, поэтому пусть u = (x² +1), тогда

Здесь d(x² +3х5) = (2x + 3)dx, поэтому пусть u = (x² +3х5), тогда

2. Метод подстановки. Пусть функция x = t монотонна и непрерывно дифференцируема в интервале (; ), и функция f(x) непрерывна в интервале (а; b), где а =  b = Тогда верна формула

 f(x) dx =  f(t)tdt . (50)

Пример 5. Найти следующие интегралы.

1).  е^3х dx. Этот интеграл сводится к табличному интегралу 3 заменой: 3х = t. Отсюда х =  , х = ( )=  . Тогда, по формуле (50), данный интеграл равен е^t( ) dt = ( )е^t + c. Теперь, делается обратная замена t на –3х, и получается:  =  е ^3х + c.

Делается замена: 2х  1= t, отсюда: х = , dx = dt, х1 = , . Тогда

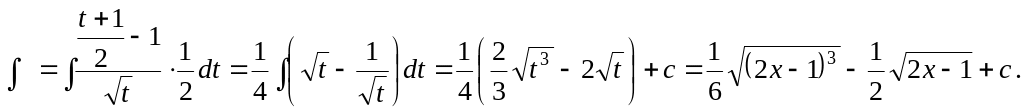
Делается замена: ln x = t, отсюда x = e^t, dx = e^tdt. Тогда

4).

Выделяется полный квадрат в знаменателе: х² +4х+3 = (х² +4х+4)  1

= (х + 2)² 1. Делается замена: (х + 2) = t, отсюда dx = dt и х² + 4х+3 = t²  1.

3. Метод интегрирования по частям. Если u и v  дифференцируемые функции от х, то верно равенство

 u dv = u v  v du . (51)

Эта формула применяется в случаях, когда подынтегральная функция является произведением алгебраической и трансцендентной функций, напри­мер, хⁿе^х dх или хⁿlnx dх. При этом, в интеграле хⁿе^хdх в качестве u нужно при­нять хⁿ, и тогда dv = е^хdх, а в интеграле хⁿlnxdх в качестве u нужно принять lnx, и тогда dv = хⁿdх.

Пример 6. Найти следующие интегралы.

1).  хln(x +1) dх.

Применяется метод интегрирования по частям. Пусть u = ln(x +1) и dv = х dх, тогда du = (ln(x +1))dх = dх, v = х dх = , (здесь можно считать, что с = 0). Теперь, применяется формула (51):

2).  хе^2х dх. Применяется метод интегрирования по частям. Пусть u = x и dv = е^2хdх, отсюда du = dх, v = е^2х dх =  е^2х (этот интеграл находится так же, как интеграл примера 5.1)). Теперь, применяется формула (51):  = х( )е^2х   ( )е^2х dх =  хе^2х  е^2х+ с.