С войства определенного интеграла

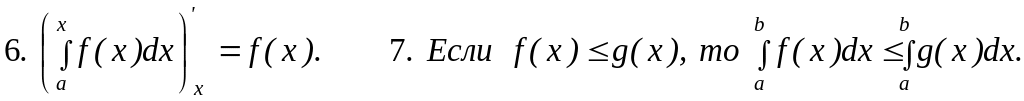
Здесь подразумевается, что интегралы, указанные в правых частях пунктов 2 5, существуют; и в пункте 7 неравенство функций рассматрива­ется на [a; b].

Т еорема 2. Пусть f(x) непрерывна на [a; b]. Тогда она имеет первообразную F(x) на [a; b] и верна формула:

Эта формула называется формулой Ньютона-Лейбница. Она означает, что определенный интеграл от непрерывной функции равен разности значе­ний первообразной функции при верхнем и нижнем пределах интегрирова­ния. Эта разность называется приращением F(x) на [a; b] и обозначается:

П ример 8. Вычислить определенные интегралы.

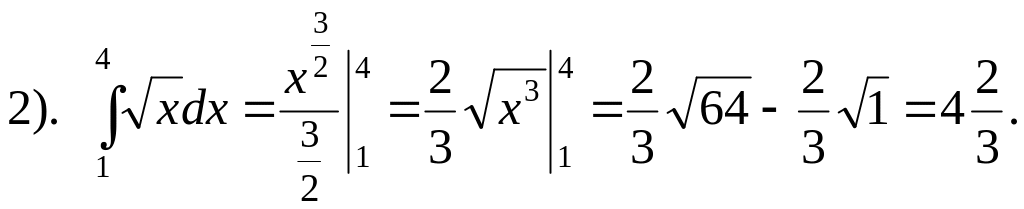
Т еорема о среднем. Если функция f(x) непрерывна на [a; b], то между a и b найдется число с такое, что выполняется равенство:

Величина f(c) называется средним значением функции f(x) на [a; b].

Пример 9. Определить среднее значение функции у = х² на [1; 3].

Здесь f(x) = x² . Вычисляется интеграл:

Т еперь, из теоремы о среднем, получается:

Вывод: среднее значение приближенно равно 4,667 при х  2,1602.

Из теоремы 2 следует, что для непрерывных функций методы интег­риро­вания для неопределенного интеграла можно применять и для опреде­ленного интеграла со следующими дополнениями.

В методе интегрирования подстановкой формула (50) принимает вид:

(55)

В методе интегрирования по частям формула (51) принимает вид:

П ример 10. Вычислить следующие определенные интегралы.

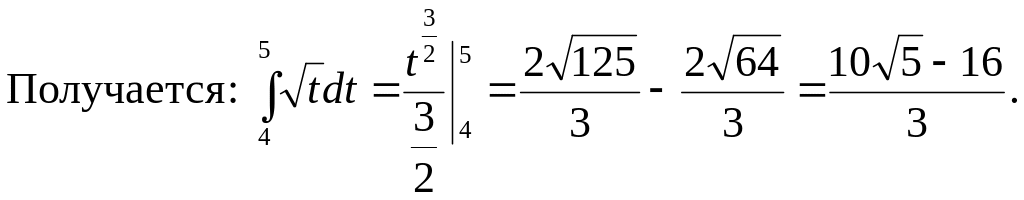
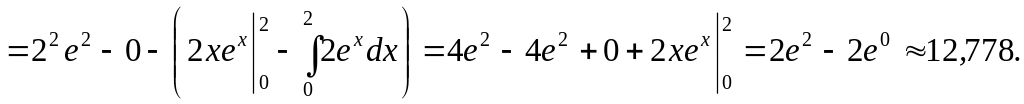
§4. Применение определенных интегралов

1. Площадь плоской фигуры (см. черт. 41), ограниченной кривыми y = f(x), y = g(x) и прямыми x = a, x = b (при этом f(x) < g(x), a < b) вычисляется по формуле:

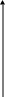
y y = g(x)

y = f(x)

0 a b x

Черт.41.

2. Площадь плоской фигуры (см.черт.42), ограниченной кривыми x = F(y), x = G(y) и прямыми y = c, y = d (при этом F(y) < G(y), c < d) вычисляется по фор­муле:

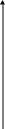
y

d

x = F(y) x = G(y)

c

0 x

Черт.42.

Пример 11. Вычислить площадь фигуры, ограниченной линиями:

y = x² +1, y = x, y = 5, x = 0.

Решение. y = x² +1 – это уравнение параболы с вершиной С(0; 1);

y = x  это прямая, проходящая через начало координат под углом 45^о к оси Ох; x = 0 это ось Оy. Получается фигура ОСАВ (см. черт. 43).

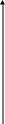
у

5 А В

D

1 С E

х

0 2 5

Черт.43.

Требуется найти площадь фигуры АВОС.

Вычисляются координаты точек пересечения А, В:

y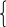 = x, y = x² +1,

y = 5,  В(5; 5). y = 5,  А(2; 5).

Так как граница фигуры неоднородная, то фигура АВОС разбивается на две части ОСАD и DAB. Площадь первой части равна:

П лощадь второй части равна:

Площадь всей фигуры АВОС равна 8/3 + 4,5  7,167.

Пример 12. Вычислить площадь фигуры, ограниченной линиями

y = x², хy = 8, y = 9.

Решение. y = x² – это уравнение параболы с вершиной 0(0; 0);

хy = 8  это уравнение гиперболы, y = 9  уравнение прямой, параллельной оси Ох. По­лучается фигура АВС (см. черт.44).

у А В

9 у = 9

4 С

x=y x=8/y

0 2 3 х

Черт.44.

Применяется вторая формула для вычисления площадей. Переменная у считается не­зависимой, она принимает значения от у_С до 9. Вычисляются координаты точки С(х_С; у_С):

y = x²,

хy = 8,  С(2; 4).

Тогда 4  y  9. Границы фигуры АВС выражаются как функции от у: х = 8/у левая граница СА, х = у  правая граница СВ. Тогда

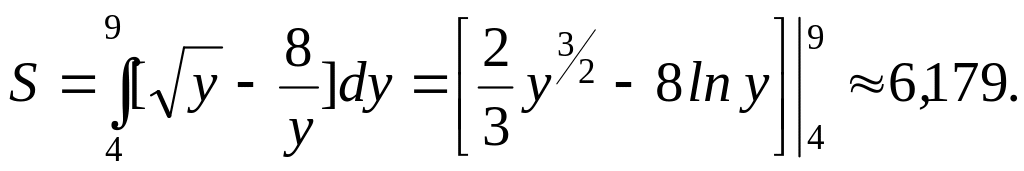
3 . Рассматривается плоская фигура, ограниченная кривыми y = f(x), y = g(x) и прямыми x = a, x = b (при этом 0  f(x) < g(x), a < b). Эта фигура вращается вокруг оси Ох, тогда объем V тела, ограниченного поверхностью вращения вычисляется по формуле:

4. Рассматривается плоская фигура, ограниченная кривыми x = F(y),

x = G(y) и прямыми y = c, y = d (при этом 0  F(y) < G(y), c < d). Эта фи­гура вращается вокруг оси Оу, тогда объем V тела, ограниченного поверхно­стью вращения вычисляется по формуле:

Пример 13. Вычислить объем тела, образованного вращением вокруг оси OY фигуры, ограниченной линиями: y = x² +1, y = x, y = 5, x = 0.

Решение. Рассматривается фигура АВОС на чертеже 43 из примера 11. Она разбивается на части АВЕС и СЕО, и вычисляются объемы тел, об­разованных вращением этих частей.

Для первого тела границы АВЕС представляются в виде: х = (у1), х = у, 1 у  5. Тогда объем V₁ первого тела равен:

Для второго тела границы СЕО имеют вид: х = у, х = 0, 0 у  1. Тогда объем V₂ второго тела равен:

Объем всего тела вращения равен 104,720 + 1,047 = 105,767.