
- •Глава 7. Интегральное исчисление
- •§1. Неопределенный интеграл
- •Свойства интегралов
- •§2. Методы интегрирования
- •4. Интегрирование рациональных функции. Следующие функции называются простейшими рациональными дробями:
- •§3. Определенный интеграл
- •С войства определенного интеграла
- •§4. Применение определенных интегралов
- •§5. Несобственные интегралы
- •Упражнения
4. Интегрирование рациональных функции. Следующие функции называются простейшими рациональными дробями:
![]()
Интегрирование таких функций осуществляется следующим образом.
1).
![]() 2).
2).
![]()
3).
![]() Сначала
выделяется полный квадрат в знаменателе:
Сначала
выделяется полный квадрат в знаменателе:
![]() =
=![]() =
=![]()
Теперь,
делается замена:
![]() ,
отсюда
,
отсюда
![]() Тогда
Тогда
![]() где
где
![]()
![]() =
=
![]()
![]()
![]() =
=
![]()
![]() =
=![]()
4).
![]() С помощью той же замены
С помощью той же замены
![]() при n
> 1 получается:
при n
> 1 получается:
![]()
![]()
a).
Первое слагаемое вычисляется с помощью
замены
![]() ,
,
![]() :
:
![]()
![]() =
=![]()
б). Второе слагаемое вычисляется методом интегрирования по частям. Пусть
![]() .
Тогда
.
Тогда
![]() .
.
Пусть
![]() тогда
тогда
![]()
По
формуле (51),
![]()
Получилось так называемое рекуррентное соотношение для интеграла In :
![]()
Это соотношение позволяет последовательно вычислить In для любого n.
Пример 7. Найти следующие интегралы.
1).
![]()
2).
![]()
=
![]()
3).
![]() Здесь
Здесь
![]()
![]()
![]()
E=![]() .
Так как D
< 0, то
.
Так как D
< 0, то
![]()
+
11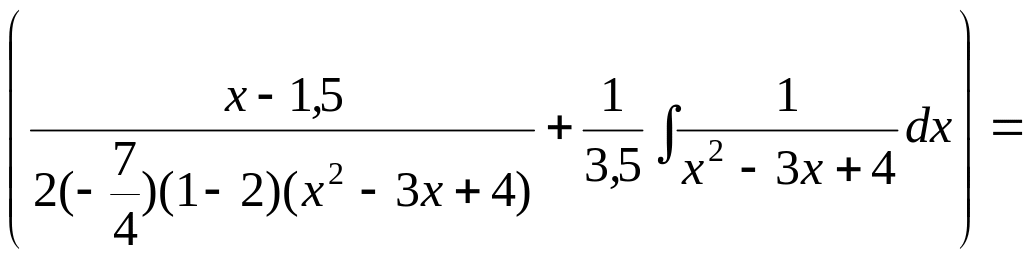
![]()
![]()
5. Интегрирование некоторых тригонометрических функций. Следующие интегралы демонстрируют основные приемы интегрирования тригонометрических функций.
1).
Интегралы
![]() используют тригонометрические формулы
преобразования произведения в сумму
(см. главу 4 §2).
используют тригонометрические формулы
преобразования произведения в сумму
(см. главу 4 §2).
а).
![]()
=
![]()
![]()
б).
![]()
=
![]()
![]()
в).
![]()
=
![]() +
+
![]()
2).
Интегралы
![]() используют тригонометрические формулы
понижения степени, (см. главу 4 §2).
используют тригонометрические формулы
понижения степени, (см. главу 4 §2).
а).
![]()
б).
![]()
в).
![]()
3).
Интегралы вида
![]() используют замены sinmx
= t,
cosmx
= t,
соответственно.
используют замены sinmx
= t,
cosmx
= t,
соответственно.
а).
![]()
б).
![]()
§3. Определенный интеграл
Пусть функция f(x) определена на отрезке [a; b]. Этот отрезок разбивается на n частей точками: а = х0 < x1 < x2< … < xn = b, и пусть x1, x2, …, xn длины отрезков разбиения. Из каждого такого отрезка
(xi; xi) выбирается произвольная точка i , вычисляется значение f(i), и составляется сумма
S1 = f(1)x1 + f(2)x2 + … + f(n)xn . (52)
Эта сумма называется интегральной суммой для f(x) на [a; b], более кратко она записывается в виде
S1 =
![]() .
.
Затем, отрезки (xi; xi) разбиваются на более мелкие части, из них выбираются новые точки и составляется новая интегральная сумма S2 вида (52). Этот процесс разбиения отрезка [a; b] на более мелкие части, и составление соответствующих интегральных сумм продолжается бесконечно. В результате возникает бесконечная последовательность интегральных сумм: S1, S2, S3, … .
Определение 3. Определенным интегралом от функции f(x) в пределах от а до b называется предел указанных выше интегральных сумм, когда отрезок [a; b] бесконечно измельчается, если этот предел существует и не зависит от способов разбиения и выбора точек.
Обозначение:
![]()
Числа a, b называются пределами интегрирования.
Понятие интегральной суммы
иллюстрируется на чертеже 40. Рассматривается
непрерывная положительная функция y
= f(x)
на [a; b].
Ее график и ось Оx образуют
криволинейную трапецию аАВb.
Через точки деления а, x,
x2,
…, xn,
b проведены отрезки,
параллельные оси ОY
, и образованы прямоугольники с
основаниями
![]() и высотами f(1),
f(2),
…, f(n).
и высотами f(1),
f(2),
…, f(n).
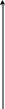
y f (n) В




 f
(2) y
= f(x)
f
(2) y
= f(x)
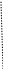


 f(1)
f(1)
 А …
А …

 x
x
0 a 1 x1 2 x2 . . . xn-1 n b
Черт.40.
Тогда площади этих прямоугольников равны f(1)x1, f(2)x2 , …, f(n)xn, соответственно, и их сумма f(i)xi является приближенным значением площади всей криволинейной трапеции аАВb. Если производить более мелкие разбиения [a; b], то соответствующие суммы f(i)xi будут приближаться к истинному значению площади аАВb. Поэтому площадью криволинейной трапеции аАВb назван предел указанных сумм f(i)xi, когда отрезок [a; b] бесконечно измельчается. С другой стороны, эти суммы являются интегральными суммами для функции f(x) на [a; b]. Тем самым, получен следующий геометрический смысл определенного интеграла:
Определенный интеграл положительной функции y = f(x) по отрезку [a; b] равен площади криволинейной трапеции аAВb.
