§7. Уравнение плоскости в пространстве

1. Уравнение плоскости, проходящей через данную точку. Положение плоскости в пространстве однозначно определяется точкой, лежащей на плоскости, и вектором, перпендикулярным этой плоскости. Пусть точка М₀(х₀, у_0, z₀) лежит на плоскости , вектор n = {A, B, C} перпендикулярен  и М(х, у_, z) – текущая точка. Тогда М(х, у_, z) принадлежит  тогда и только тогда, когда вектор перпендикулярен n. Здесь имеет координаты {х  х₀, у у_0, z  z₀}, и, с помощью условия перпендикулярности векторов, это утверждение записывается следующим образом:

М  n = 0  A(х  х₀) + В(у у₀) + С(z  z₀) = 0. (34)

Правое равенство называется уравнением плоскости, проходящей через данную точку. Оно является линейным уравнением относительно переменных х, у, z.

2. Общее уравнение плоскости. Любое уравнение, линейное относительно х, у, z , задает плоскость в пространстве:

Aх + Ву + Сz + D = 0, (35)

где коэффициенты A, B, C не равны 0 одновременно.

Это уравнение называется общим уравнение плоскости. При этом вектор n = {A, B, C} перпендикулярен этой плоскости и называется нормалью плоскости. Величина равна расстоянию от начала координат до этой плоскости.

Исследование уравнения (35) сводится к рассмотрению следующих случаев:

1) если коэффициент A = 0, то Ву + Сz + D = 0 – уравнение плоскости, параллельной оси ОХ;

2) если коэффициент В = 0, то Ах + Сz + D = 0 – уравнение плоскости, параллельной оси ОY;

3) если коэффициент C = 0, то Ах + By + D = 0 – уравнение плоскости, параллельной оси ОZ;

4) если D = 0, то Aх + Ву + Сz = 0  уравнение плоскости , проходящей через начало координат.

В частности, уравнения координатных плоскостей XOY, XOZ и YOZ имеют вид z = 0, у = 0 и х = 0 соответственно.

3. Угол между плоскостями. Угол между двух плоскостей - это угол между нормалями этих плоскостей. Пусть две плоскости_ и _ заданы уравнениями A₁х + В₁у + С₁z + D₁ = 0 и A₂х + В₂у + С₂z + D₂ = 0, тогда n₁ = { A₁; В₁; С₁} и n₂ = { A₂; В₂; С₂} - нормали этих плоскостей. Согласно свойству 8 скалярного произведения, угол  между _ и _ находится по формуле:

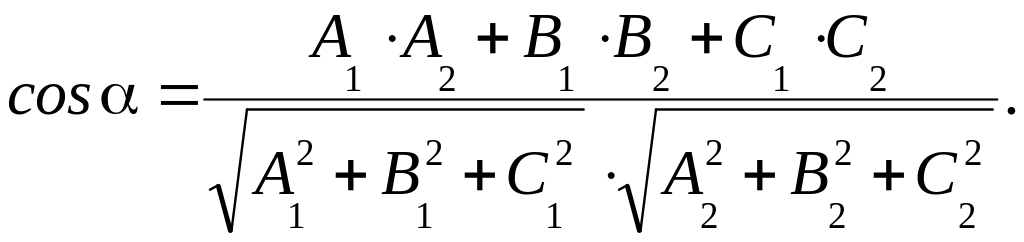(36)

Теперь, из соответствующих свойств векторов получаются следующие соотношения.

Условие перпендикулярности плоскостей:

Условие параллельности плоскостей:

4. Расстояние от точки до плоскости. Расстояние d от точки М₁(х₁, у_1, z₁) до плоскости, задаваемой уравнением (35), вычисляется по следующей формуле:

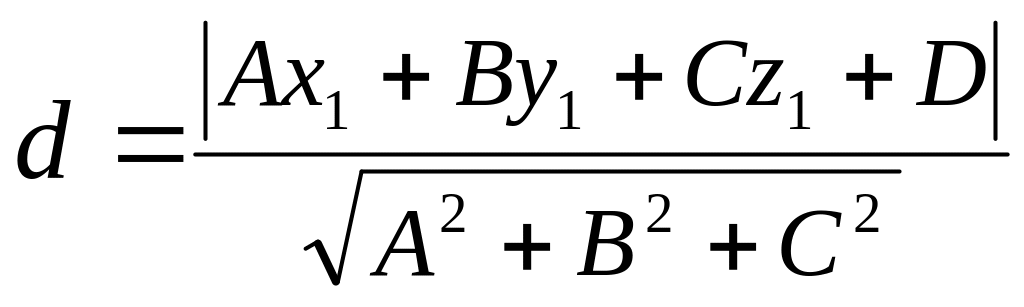. (37)

5. Задачи на плоскость. При решении задач на построение уравнения плоскости можно руководствоваться следующими инструкциями.

Основное правило. Чтобы написать уравнение плоскости надо найти точку М₀, лежащую на плоскости, и вектор n, перпендикулярный искомой плоскости. Затем координаты этой точки и этого вектора подставляются в (34). Точка часто дается в условии задачи. А чтобы найти нормальn, достаточно взять два вектораа иb, лежащих в этой плоскости или параллельных ей. В этом случае в качестве n можно взять векторное произведение а b.

Пример 22. Даны точки М₁(3; 1; 0) и М₂(5; 3; 1). Написать уравнение плоскости, проходящей через точку М₁ перпендикулярно вектору .

Решение. Применяется формула (34). Здесь в качестве М₀ берется точка М₁, а в качестве нормалиn берется вектор = {5  3; 3 + 1; 1  0} =

{2; 4; 1}. Тогда, согласно основному правилу, получается искомое уравнение:

2(х – 3) + 4(у + 1) + (z – 0) = 0 или 2х + 4у +z 2 = 0.

Пример 23. Написать уравнение плоскости, проходящей через точку М₀(1; 2; 3) и параллельно плоскости 4x – 3y + 2z – 1 = 0.

Решение. Применяется формула (34). Точка М₀ дана в условии задачи. Кроме того, по условию, искомая плоскость параллельна данной плоскости, тогда у этих плоскостей одинаковая нормальn ={4; -3; 2}. Теперь, согласно основному правилу, получается следующее искомое уравнение:

4(x – 1)  3(y  2) + 2(z  3) = 0 или 4x 3y +2z – 4 = 0.

Пример 24. Написать уравнение плоскости, проходящей через ось ОZ и точку М₀(3; 2; 0).

Решение. Применяется формула (34). Точка М₀ дана в условии задачи, но нормальn явно не дана. Поэтому надо найти два вектора, лежащих в этой плоскости. Такими векторами в данном случае являются ортаk = {0; 0; 1} оси ОZ и радиус-вектор = {3; 2; 0}. Тогда, согласно основному правилу,

n = Следовательно, A = 2, B = 3, C = 0, и получается следующее искомое уравнение: 2(х  3) +3(у + 2) = 0 или 2х + 3у = 0.

Пример 25. Написать уравнение плоскости, проходящей через три точки М₁(2; 1; 1), М₂(3; 2; 1), М₃(1; 0; 3).

Решение. Применяется формула (34). В качестве М₀ берется точка М₁, а чтобы найти нормальn берутся два вектора и , которые лежат в искомой плоскости. Здесь и . Тогда нормальn равна векторному произведению этих векторов:

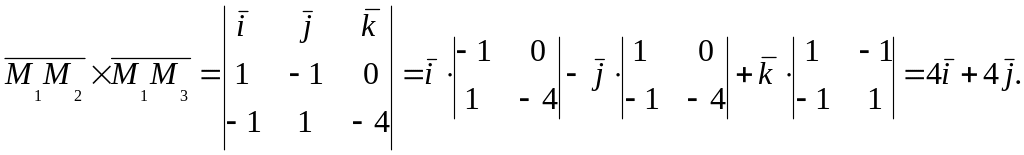
Получилосьn = Следовательно, A = 4, B = 4, C = 0. Найденные значения подставляются в (34), получается 4(х  2) +4(у + 1) = 0 или 4х + 4у  4 = 0 – уравнение искомой плоскости.

Пример 26. Найти угол между плоскостями:

.

Решение. Здесьn₁ = {2; -2; 1} иn₂ = {1; 0; 1}, тогда, по формуле (36), 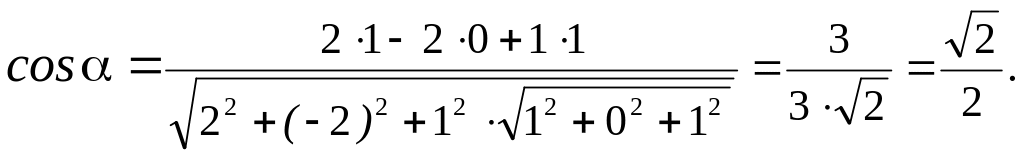Cледовательно, ^o .

Пример 27. Найти расстояние от точки (1; 1; 5) до плоскости 2x + 2y – z  4 = 0.

Решение. Применяется формула (37), искомое расстояние равно