§ 5. Линейные неоднородные дифференциальные уравнения второго порядка
Рассмотрим основные свойства решений линейного неоднородного дифференциального уравнения второго порядка (20):
.
Имеет место следующая теорема.
Теорема. Общее решение уравнения (20) есть сумма любого его частного решения и общего решения соответствующего однородного уравнения.
Таким образом , чтобы найти общее решение линейного неоднородного уравнения, нужно найти общее решение соответствующего однородного уравнения и какое-нибудь частное решение неоднородного уравнения. В общем случае задача отыскания частного решения является сложной. Покажем, как можно найти частное решение неоднородного уравнения методом вариации произвольных постоянных, если известно общее решение соответствующего однородного уравнения.
Пусть
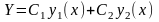- общее решение однородного уравнения
.
Будем искать частное решение неоднородного
уравнения (20) в виде
|
(24) |
,рассматривая и как некоторые ископаемые функции от . Продифференцируем последнее равенство
|
(25) |
,Подберем
функции
так, чтобы выполнялось равенство
|
(26) |
.Тогда равенство (25) принимает вид
.
Дифференцируя
это равенство, найдем
:
.
Подставляя
выражения для
и
в уравнение (20) и группируя слагаемые,
получаем
Выражения
в квадратных скобках равны нулю, так
как
и
- решения однородного уравнения. Поэтому
последнее равенство принимает вид
|
(27) |
Таким
образом, функция (24) является решением
уравнения (20), если функции
и
удовлетворяют уравнениям (26) и (27).
Объединяя их, получаем систему уравнений
|
(28) |
в
которой
и
- неизвестны,
,
,
,
и
- известны. Так как определителем этой
системы является определитель Вронского
,
составленный
из линейно независимых решений
и
однородного уравнения (21), то он по
теореме (об определителе Вронского,
составленном из линейно независимых
решений) не равен нулю, а значит, система
(28) имеет единственное решение относительно
и
.
Решая эту систему, получаем
,
где
и
- известные функции, откуда, интегрируя,
найдем
и
.
Подставляя полученные выражения для
и
в равенство (24), получаем искомое частное
решение уравнения (20).
Пример.
Найти частное решение уравнения
.
Общее
решение данного уравнения
соответствующего однородного уравнения
.
Поэтому частное решение неоднородного
уравнения будем искать в виде
|
(29) |
.Система (28) для нахождения и в данном случае имеет вид
Складывая
эти уравнения, найдем
.
Отсюда, интегрируя, получаем
.
Произвольную
постоянную не пишем, так как ищем
какое-нибудь частное решение. Подставляя
выражение
в первое из уравнений системы, найдем
,
откуда, интегрируя, получаем
.
Подставляя
найденные выражения
и
в равенство (29), получаем частное решение
данного неоднородного уравнения:
.
Заметим,
что, найдя частное решение неоднородного
уравнения и зная общее решение
соответствующего однородного уравнения,
на основании равенства
можно записать общее решение данного
неоднородного уравнения:
,
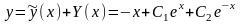где и - произвольные постоянные.