4. Складний рух точки

4.1. Довідкові дані

При складному русі розглядаємо рух точки відносно деякої системи відліку, яка в свою чергу рухається відносно якоїсь іншої системи відліку, умовно прийнятої за нерухому тобто можна вважати, що точка одночасно бере участь у двох рухах.

Рух даної точки відносно рухомої системи відліку називається відносною, а швидкість та прискорення – відносними ( ).

Рух рухомої системи відліку відносно нерухомої називається переносним, а швидкість та прискорення точки рухомого середовища, з якою в даний момент часу збігається рухома точка називаються переносними ( ).

Рух точки відносно нерухомої системи відліку називається абсолютним або складним, а швидкість та прискорення абсолютними ( ) (рис. 11).

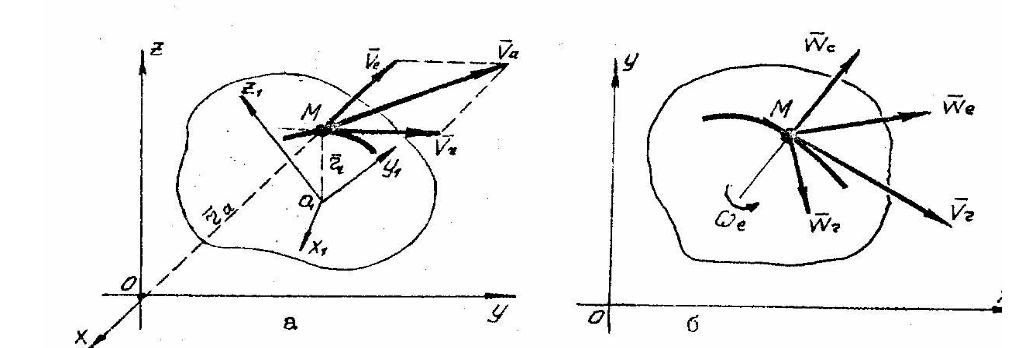
Рис. 11

Згідно з теоремою додавання швидкостей абсолютна швидкість є діагоналлю паралелограма, побудованого на швидкостях та :

.

Модуль абсолютної швидкості можна визначити за допомогою теореми косинусів або методом проекцій на осі координат.

Абсолютне прискорення визначається за теоремою додавання прискорень (теоремою Коріоліса):

,

де ) - прискорення Коріоліса (поворотне).

Модуль прискорення Коріоліса а його напрямок визначається за правилом векторного добутку, або за правилом Жуковського (проекцію на площину, перпендикулярну вісі переносного обертання, повертаємо на 90⁰ у напрямку цього обертання. Це і є напрямок прискорення Коріоліса).

Якщо переносний рух поступальний та прямолінійний, то абсолютне прискорення визначається за формулою:

.

Модуль визначають за його проекціями на осі координат.

4.2. Задача № 3

Визначити абсолютну швидкість та абсолютне прискорення точки М в момент часу , якщо відомі закон переносного руху тіла та відносна її швидкість радіус R = 1 м (Рис. 12).

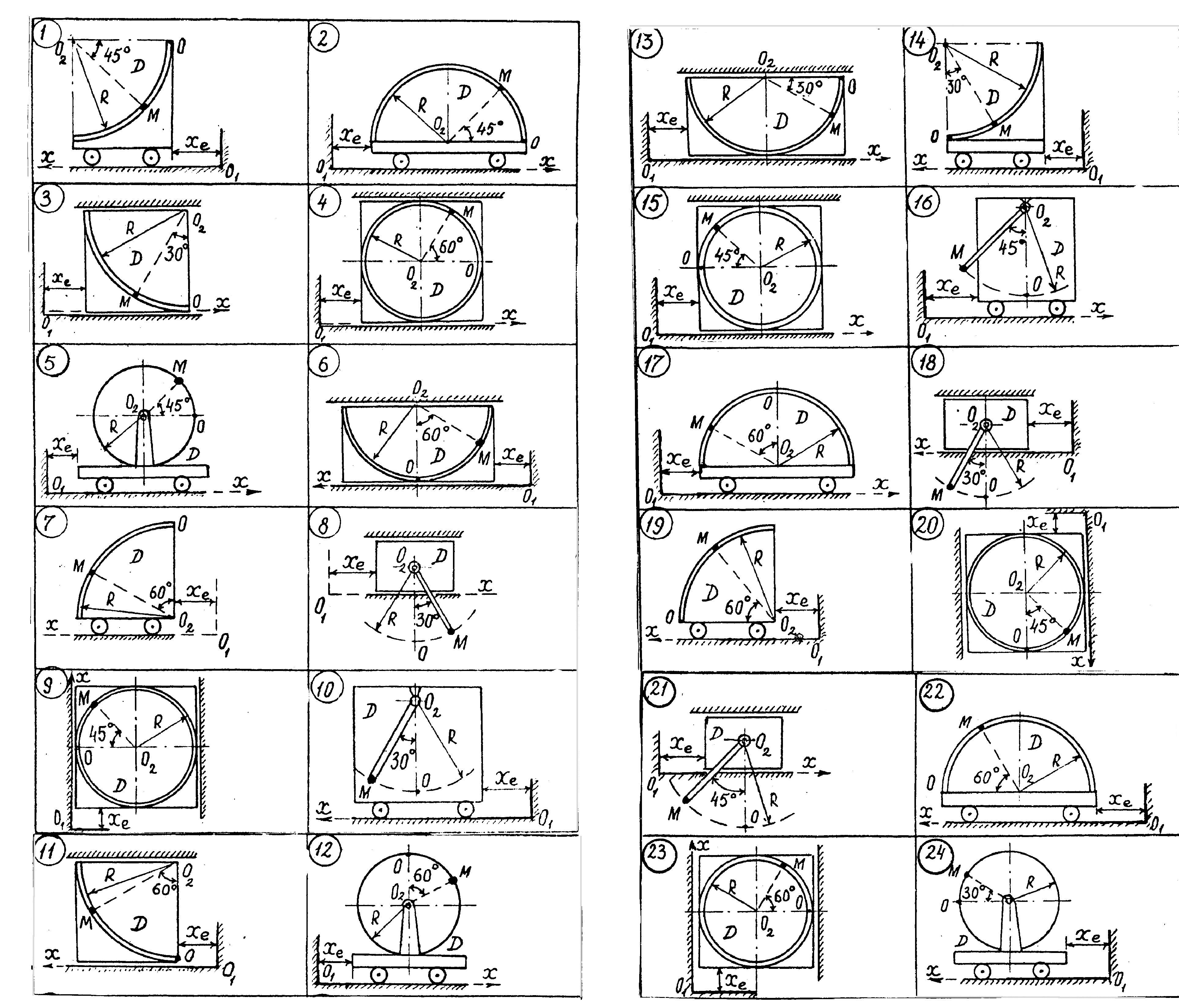
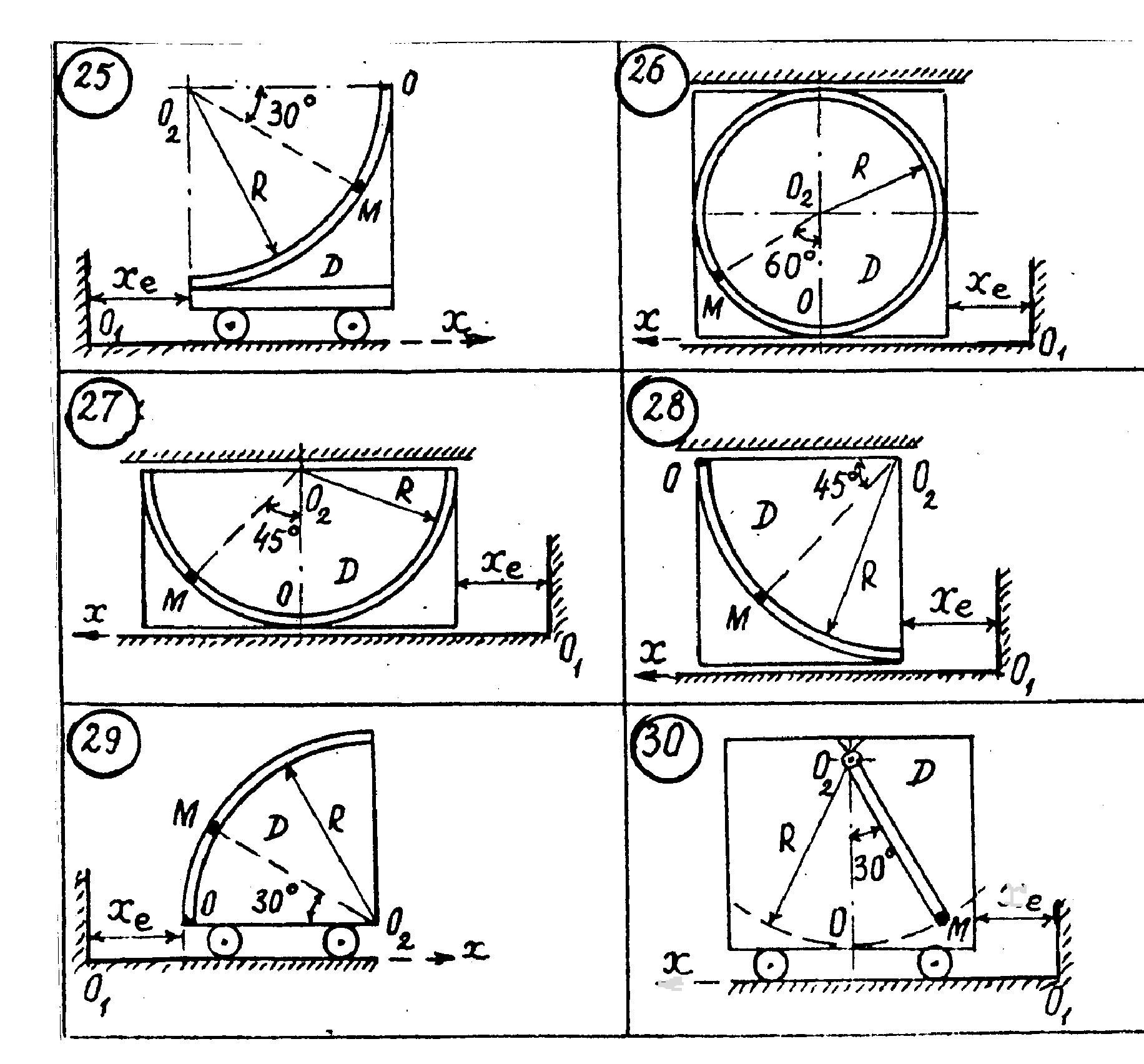
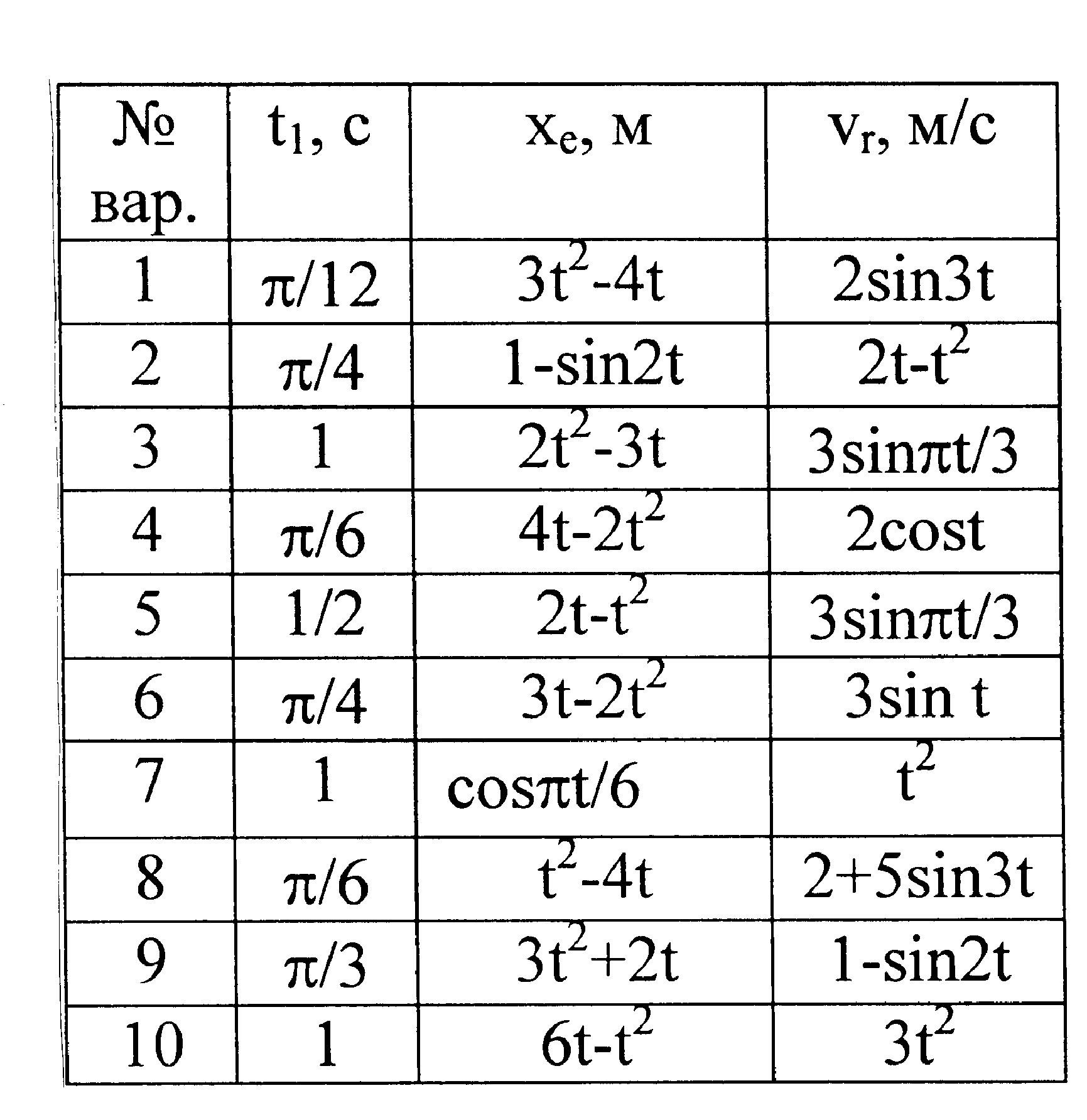
Рис.12

3. Приклад розв’язку задачі.

Задача. За заданим рухом тіла D: ( – в м, - в сек) та відносною швидкістю ( - в м/с, - в сек) визначити абсолютну швидкість та абсолютне прискорення точки М, якщо = 1 м, = 30⁰, (рис. 13)

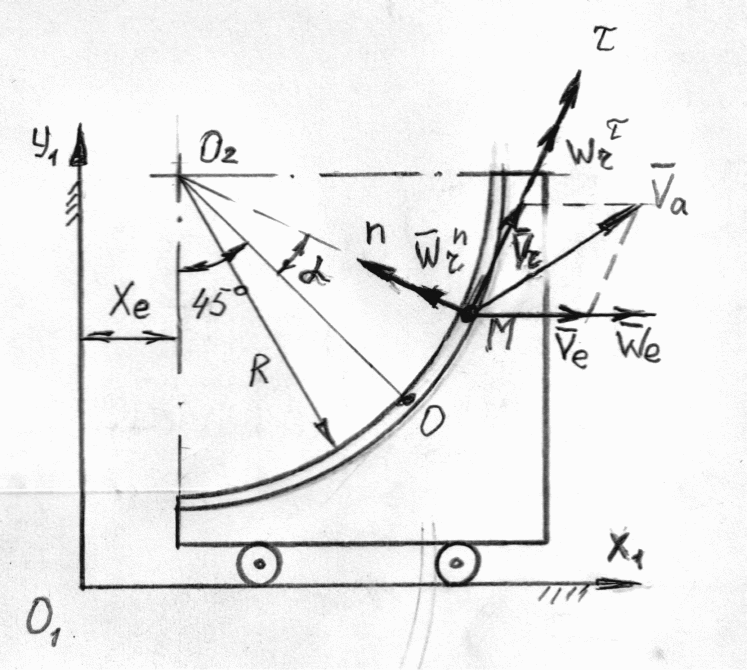
Рис. 13

Розв’язок.

1. Метод розв’язку задачі – складний рух точки.

2. Аналізуємо характер руху об’єктів за ланцюжком точка – рухоме середовище – нерухомий об’єкт, що дає змогу чітко визначити абсолютний, відносний та переносний рухи. В даній задачі ланцюжок має вигляд:

відносний рух переносний рух

точка М --------- тіло D -------- Земля

а бсолютний рух

Зауваження: Рухомих середовищ між точкою та Землею може бути декілька; відповідно буде і декілька переносних рухів.

3. Умовно зупиняємо переносний рух і визначаємо кінематичні параметри відносного руху точки.

Відносний рух – криволінійний по дузі кола радіуса із швидкістю .

а). Малюємо точку М на тілі D в заданому положенні.

Рух точки задано натуральним способом. Тому відкладаємо = 30⁰ від початкового положення точки (від точки О) в додатньому напрямку і проводимо від неї натуральні осі . (Вісь спрямовуємо по дотичній до траєкторії в точці М додатному напрямку, а вісь - перпендикулярно до дотичної в середину траєкторії).

б). Відносна швидкість точки при c

м/с.

Вектор спрямовуємо по дотичній до траєкторії в точці М в додатньому напрямку.

в). Відносне прискорення точки при с

,

де м/с²; м/с.

Будуємо вектори та , не визначаючи повне відносне прискорення.

4. Умовно зупиняємо відносний рух точки і визначаємо кінематичні характеристики переносного руху.

Переносний рух поступальний прямолінійний за законом .

Рух заданий координатним способом. Тому вибираємо нерухому декартову систему координат .

а). Положення тіла D в момент часу c

м.

Відкладаємо = 1,41 м вздовж осі х₁ в додатному напрямку і малюємо в масштабі тіло D.

б). Переносна швидкість, тобто швидкість тієї точки рухомого середовища - тіла D, в якій в даний момент часу знаходиться рухома точка М.

при с м/с.

Вектор прикладаємо в точці М і спрямовуємо його в додатньому напрямку паралельно осі х₁.

в). Переносне прискорення

при с м/с².

Вектор прикладаємо в точці М і спрямовуємо його в додатньому напрямку паралельно осі х₁ (знак “-“ будемо враховувати при кількісних підрахунках).

5. Абсолютний рух.

а). Абсолютна швидкість точки М

.

Модуль абсолютної швидкості

= = 3,25 м/с.

Вектор за модулем і напрямком є діагоналлю паралелограма, побудованого із векторів та .

б). Абсолютне прискорення

.

Прискорення Коріоліса = 0, тому що = 0.

Тоді відповідно до пп. 2, 3 запишемо

.

Спроектуємо одержане рівняння на осі та підрахуємо:

м/с²;

м/с².

Модуль абсолютного прискорення

= = 3,89 м/с².

Спрямувати вектор можна за його проекціями на осі .

6. Відповідь.

Абсолютна швидкість точки = 3,25 м/с, абсолютне прискорення = 3,89 м/с².