
- •Кафедра теоретичної механіки
- •Довідкові дані..............................................................................................10
- •Довідкові дані..............................................................................................14
- •Поступальний та обертальний рух тіла
- •2.1. Довідкові дані
- •2.2 Задача № 1
- •Плоский рух твердого тіла
- •3.1. Довідкові дані
- •Складний рух точки
- •4.1. Довідкові дані
- •Література
Плоский рух твердого тіла
3.1. Довідкові дані
Плоским називається такий рух тіла, при якому всі точки тіла рухаються паралельно деякій нерухомій площині. Траєкторії всіх точок тіла є плоскими і рух тіла зводиться до руху проекції цього тіла на певну площину.
Плоский рух тіла можна розглядати як суму поступального руху разом із довільно обраним полюсом А та обертального руху навколо цього полюса. Кінематичні рівняння плоского руху (рис. 6):
![]()
![]()
![]()
![]()
 Рис.
6
Рис.
6
З
цих рівнянь можна визначити швидкість
та прискорення полюса А (
![]() та
та
![]() ), кутову швидкість та прискорення
обертальної частини руху
та
.
), кутову швидкість та прискорення
обертальної частини руху
та
.
Якщо
відомі
![]() ,
,
![]() та
,
можна визначити також швидкість та
прискорення будь-якої іншої точки тіла
В.
та
,
можна визначити також швидкість та
прискорення будь-якої іншої точки тіла
В.
Швидкість точки В можна визначити трьома способами:
а) скориставшись теоремою про додавання швидкостей, будуючи паралелограм швидкостей (рис. 7,а,б):
![]() =
+
=
+![]() ,
де
,
де
![]() (напрям
(напрям
![]() );
);
б) скориставшись теоремою про проекції швидкостей точок тіла на пряму, що їх з’єднує (рис. 7, б):
![]() ;
;
в)
за допомогою миттєвого центра
швидкостей
![]() ,
який співпадає з миттєвим центром
обертання тіла (рис. 7, а,б,в):
,
який співпадає з миттєвим центром
обертання тіла (рис. 7, а,б,в):
![]() .
.
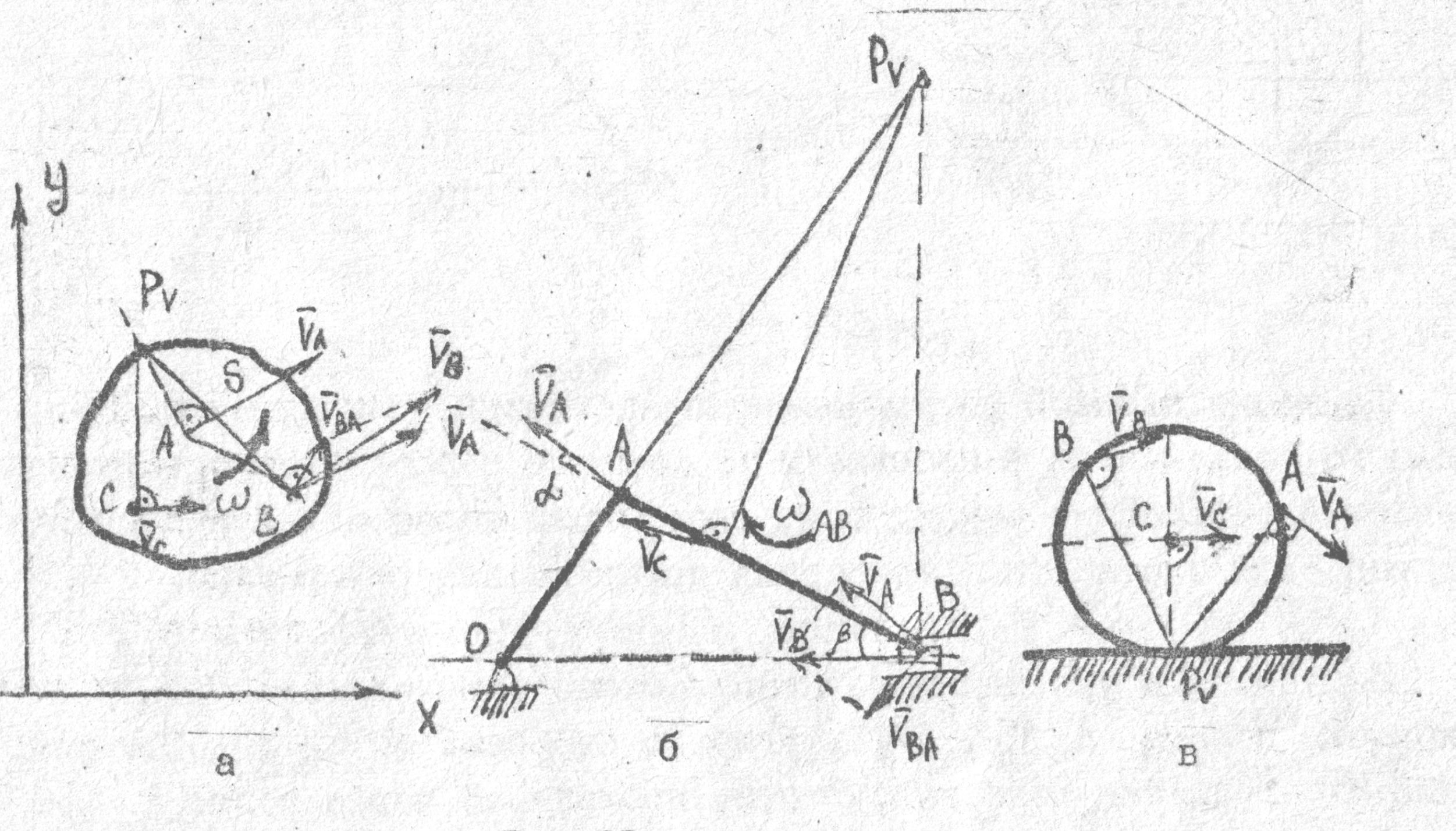
Рис. 7
Миттєвий
центр швидкостей
- це точка плоскої фігури, швидкість
якої в даний момент часу дорівнює нулеві
(![]() 0).
0).
Його положення можна визначити як точку перетину перпендикулярів до векторів швидкостей точок плоскої фігури.
Прискорення
будь-якої точки В тіла при плоскому русі
можна визначити, скориставшись теоремою
про додавання прискорень: прискорення
полюса
![]() ,
обертального
,
обертального
![]() та доцентрового
та доцентрового
![]() прискорень точки В навколо полюса
А (рис. 8):
прискорень точки В навколо полюса
А (рис. 8):
![]() ,
,
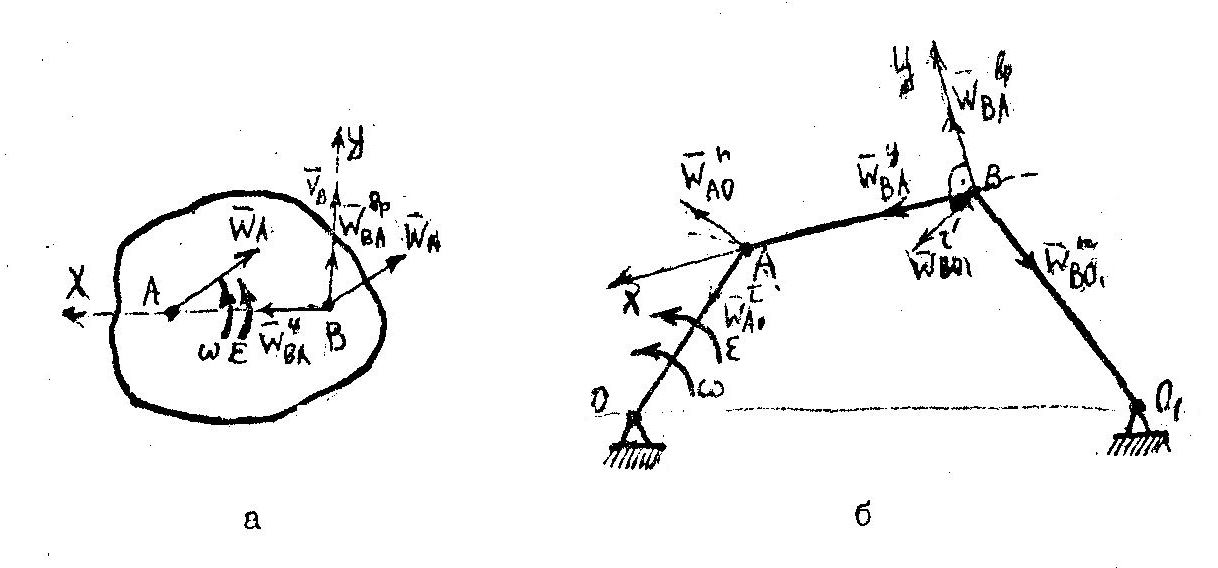 Рис. 8
Рис. 8
де
![]() (спрямоване від точки В до полюса А);
(спрямоване від точки В до полюса А);
![]() (спрямоване
(спрямоване
![]() АВ в бік
).
АВ в бік
).
Якщо траєкторії точок А та В відомі, то векторне рівняння приймає вигляд:
![]() .
.
Звичайно це векторне рівняння містить 2 невідомі (модуль або напрямок вектора). Для їх визначення проектують векторне рівняння на 2 осі, отримують 2 скалярних рівняння.
3.2. Задача № 2 (Рис. 9)
3.3. Приклад розв’язку задачі
Задача.
Визначити швидкість та прискорення
точки А на ободі колеса радіуса
= 1 м, що котиться без ковзання по нерухомій
поверхні, якщо в даний момент часу
![]() = 2 м/с,
= 2 м/с,
![]() = 1 м/с2,
= 1 м/с2,
![]() = 1500 (рис.10,а).
= 1500 (рис.10,а).
Розв’язок.
Малюємо колесо в масштабі, а точку М в заданому положенні.
Колесо – рух плоский.
Миттєвий центр швидкостей колеса знаходиться в точці контакту колеса з нерухомою поверхнею.
Кутова швидкість та кутове прискорення колеса:
![]() рад/с.
рад/с.
Аналогічно
![]() рад/с2.
рад/с2.
Напрямок
кутової швидкості, тобто напрямок
обертання колеса навколо точки
![]() ,
визначає швидкість точки С
,
визначає швидкість точки С
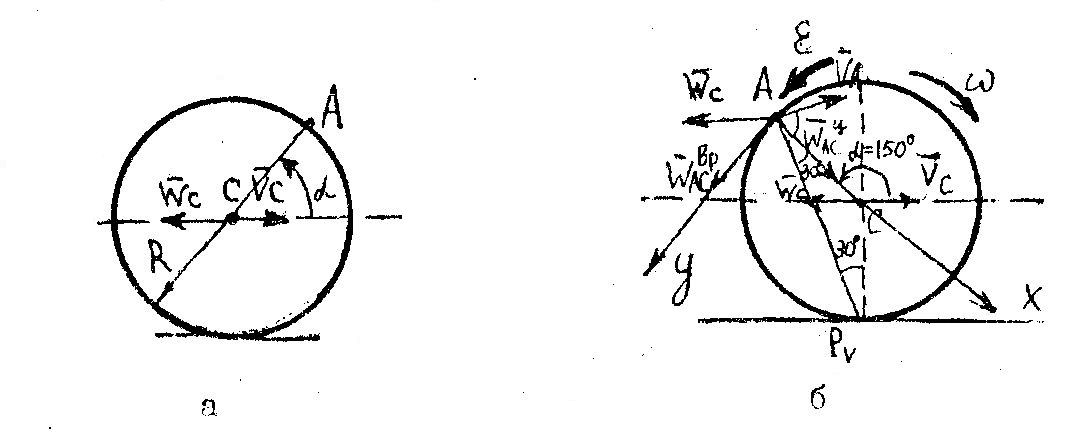
Рис. 10
Аналогічно визначається напрямок кутового прискорення.
Швидкість точки А (рис. 10,б)
![]() .
.
Миттєвий
радіус обертання визначаємо із трикутника
![]() за теоремою косинусів:
за теоремою косинусів:
![]() =
=
![]() м.
м.

Рис. 9
Тоді
![]() м/с.
м/с.
Напрямок
:
![]() в бік
.
в бік
.
Прискорення точки А
![]() .
.
а) дотичне прискорення точки А при обертанні колеса навколо полюса С
![]() м/с2 (
м/с2 (![]() в
бік
),
в
бік
),
нормальне прискорення
![]() м/с2
м/с2
(![]() спрямоване вздовж АС до точки С) (рис.
10,б);
спрямоване вздовж АС до точки С) (рис.
10,б);
б) прискорення точки С
![]()
тому що
![]() ;
;
в) прискорення точки А
Через те, що траєкторія точки А не задана (невідома), векторне рівняння приймає вигляд:
![]() .
.
Проектуємо
одержане рівняння на осі
![]() та
та
![]() (
(![]() спрямована вздовж АС,
спрямована вздовж АС,
![]() АС) рис. 10,б):
АС) рис. 10,б):
![]() м/с2;
м/с2;
![]() м/с2.
м/с2.
За проекціями визначаємо модуль прискорення точки А:
![]() =
=![]() =
=
![]() м/с2.
м/с2.
7.
Відповідь: Швидкість точки
![]() =
4,32 м/с, прискорення точки А
=
4,32 м/с, прискорення точки А
![]() =
5,57 м/с2.
=
5,57 м/с2.
