
- •Кафедра теоретичної механіки
- •Довідкові дані..............................................................................................10
- •Довідкові дані..............................................................................................14
- •Поступальний та обертальний рух тіла
- •2.1. Довідкові дані
- •2.2 Задача № 1
- •Плоский рух твердого тіла
- •3.1. Довідкові дані
- •Складний рух точки
- •4.1. Довідкові дані
- •Література
Поступальний та обертальний рух тіла
2.1. Довідкові дані
До простих рухів твердого тіла належать поступальний рух і обертальний рух навколо нерухомої вісі.
При поступальному русі будь-яка пряма, проведена в тілі, переміщується під час руху паралельно своєму початковому положенню. Всі точки тіла при поступальному русі мають однакові траєкторії, швидкості і прискорення. Тому при вивченні поступального руху тіла достатньо розглянути рух будь-якої його точки, застосувавши розрахункові формули кінематики точки. Поступальний рух тіла може бути як прямолінійним (рис. 1,б), так і криволінійним (рис. 1,а,в):
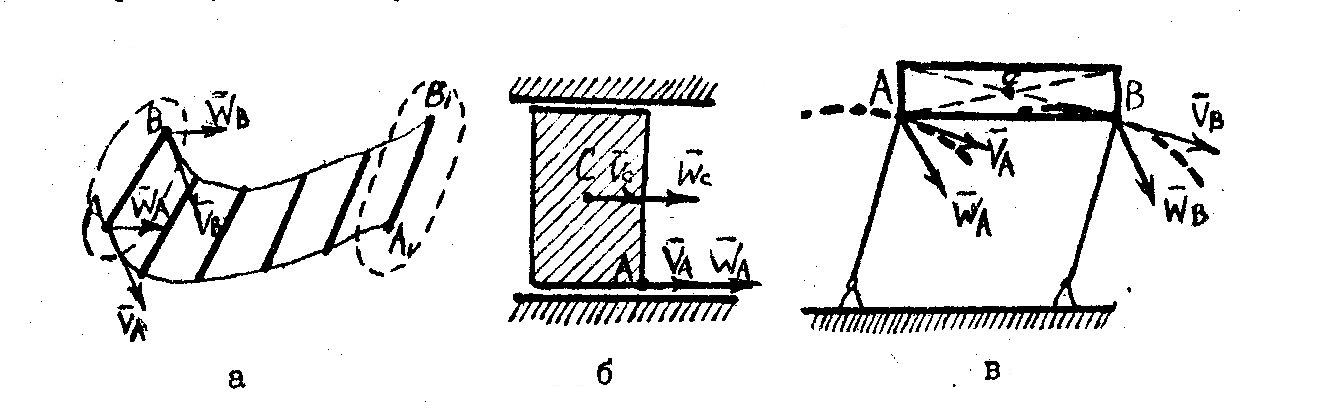 Рис.
1
Рис.
1
Обертальний рух твердого тіла навколо нерухомої осі характеризується тим, що дві точки тіла, крізь які проходить вісь обертання, залишаються весь час нерухомими. Інші точки тіла рухаються по колах відповідних радіусів в площинах, перпендикулярних вісі обертання.
![]() Положення
твердого тіла визначається кутом
повороту
Положення
твердого тіла визначається кутом
повороту
![]() ,
який являє собою закон обертання тіла.
,
який являє собою закон обертання тіла.
Загальні
кінематичні характеристики обертального
руху тіла
-
кутова швидкість
![]() (рад/с) (рис. 2,а)
(рад/с) (рис. 2,а)

Рис.2
кутове
прискорення
![]() (рад/с2).
(рад/с2).
Кутову
швидкість та прискорення позначають
на розрахункових схемах дуговими
стрілками, або векторами
![]() та
та
![]() , що напрямлені уздовж осі обертання
тіла по правилу правого гвинта.
, що напрямлені уздовж осі обертання
тіла по правилу правого гвинта.
Два найважливіших окремих випадки:
Обертання
твердого тіла рівномірне (![]() )
та рівнозмінне – прискорене або
сповільнене
)
та рівнозмінне – прискорене або
сповільнене
![]() ).
).
При
обчисленні
![]() користуються також формулою
користуються також формулою
![]() ,
,
де
N
- загальне число обертів,
![]() (для рівномірного руху, де n-число
обертів за хвилину).
(для рівномірного руху, де n-число
обертів за хвилину).
Переміщення s , швидкість v , та прискорення w будь-якої точки тіла, що знаходиться на відстані R від осі обертання, визначаються за формулами:
![]() (м) –
переміщення, (дуга траєкторії);
(м) –
переміщення, (дуга траєкторії);
![]() (м/с)
– швидкість (напрямлена по дотичній до
траєкторії, тобто перпендикулярно R
, в бік
(м/с)
– швидкість (напрямлена по дотичній до
траєкторії, тобто перпендикулярно R
, в бік
![]() ) (рис. 2,б);
) (рис. 2,б);
![]() ,
,
де
![]() (м/с2)
– дотичне прискорення (напрямлене по
дотичній
(
(м/с2)
– дотичне прискорення (напрямлене по
дотичній
(![]() в бік
в бік
![]() );
);
![]() (м/с2)
– нормальне прискорення (напрямлене
по радіусу
(м/с2)
– нормальне прискорення (напрямлене
по радіусу
![]() до осі обертання);
до осі обертання);
повне прискорення (рис. 2, б):
![]() =
=![]() .
.
Передаточні механізми призначені для перетворення обертального руху одного тіла в обертальний або поступальний рух іншого тіла (або навпаки).
Для перетворення рухів користуються зубчастими, пасовими, тросовими, фрикційними механізмами (рис. 3):

Рис. 3
Формула зв’язку при послідовному з’єднанні тіл
![]() ;
;
![]() .
.
2.2 Задача № 1
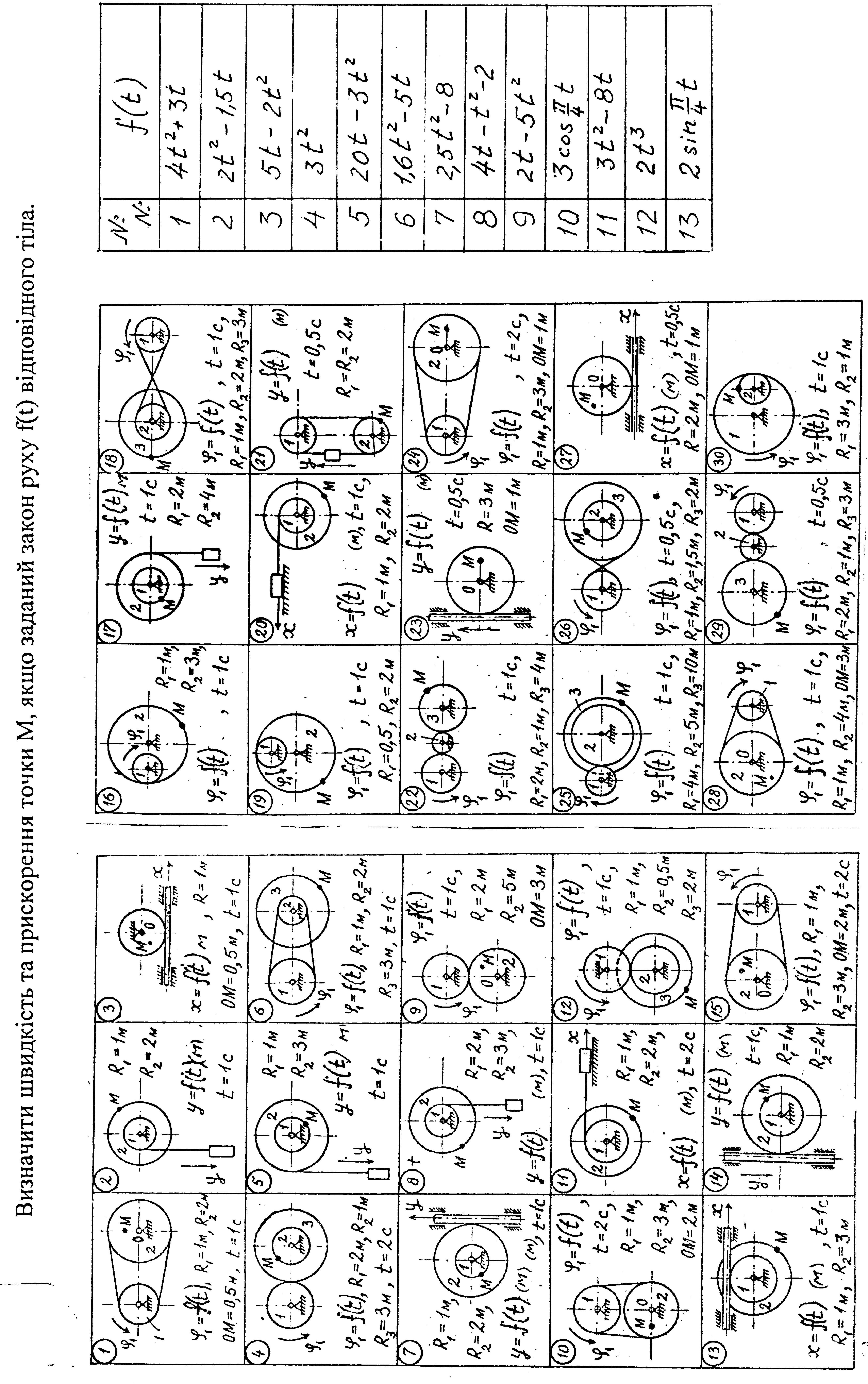
Рис.4
. Приклад розв’язку задачі
Задача.
За заданим законом обертання колеса 1:
![]() ,
(рад) визначити швидкість та прискорення
груза 4 та точки М двoхступінчастого
колеса 2 в момент часу
,
(рад) визначити швидкість та прискорення
груза 4 та точки М двoхступінчастого
колеса 2 в момент часу
![]() сек. Радіуси колес
сек. Радіуси колес
![]() =0,8
м;
=0,8
м;
![]() =1,0 м;
=1,0 м;
![]() 2=0,5
м;
2=0,5
м;
![]() 1,2
м;
1,2
м;
![]() =0,4м. Ковзання ременя по колесах відсутнє
(рис. 5).
=0,4м. Ковзання ременя по колесах відсутнє
(рис. 5).
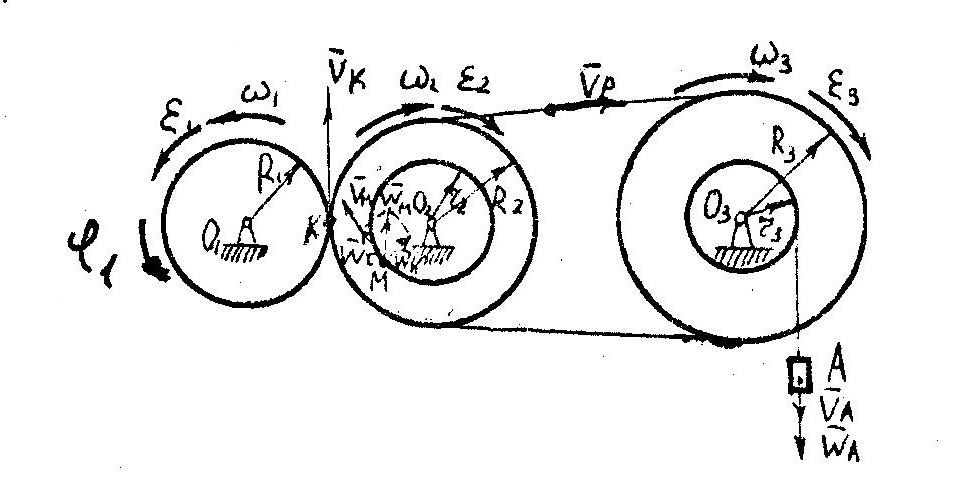
Рис. 5
Розв’язок.
Малюємо передаточний механізм в масштабі в заданому положенні і заданий додатній напрямок руху ведучого тіла механізму.
Аналіз руху тіл механізму:
колеса 1, 2, 3 – рух обертальний;
груз 4 – рух поступальний, прямолінійний.
Для розв’язку задачі необхідно використовувати формули із тем “Обертальний рух твердого тіла” та “Кінематика точки”.
Кутова швидкість та кутове прискорення колеса 1:
![]() ,
рад/с;
,
рад/с;
![]() рад/с2
.
рад/с2
.
(Напрямок
![]() та
та
![]() такий же, як і
такий же, як і
![]() ).
).
Кутова швидкість та кутове прискорення колеса 2.
На основі формул зв’язку при з’єднанні тіл в механізм – запишемо:
;
![]() .
.
Тому
![]() ,
рад/с;
,
рад/с;
![]() рад/с2 , або
рад/с2 , або
![]() рад/с2.
рад/с2.
Напрямок
швидкості точки к:
![]() в
бік
.
Відповідно напрямок кутової швидкості
в
бік
.
Відповідно напрямок кутової швидкості
![]() тіла 2 визначає швидкість (
тіла 2 визначає швидкість (![]() )
(напрямок руху) точки К.
)
(напрямок руху) точки К.
Аналогічно
визначається напрямок кутового
прискорення
![]() .
.
Швидкість точки М:
![]() .
.
При
![]() =1
с
=1
с
![]() м/с.
м/с.
Напрямок
швидкості точки М:
![]() в бік
.
в бік
.
Прискорення точки М:
![]()
Дотичне прискорення
![]() м/с2
(
м/с2
(![]() О2М
в бік
)
О2М
в бік
)
Нормальне прискорення
![]() -
-![]() м/с2
м/с2
(![]() спрямоване по радіусу О2М до центра
О2 ).
спрямоване по радіусу О2М до центра
О2 ).
Модуль прискорення:
![]() =
=![]() =
=![]() м/с2.
м/с2.
Вектор
![]() спрямований по діагоналі прямокутника,
побудованого на векторах
спрямований по діагоналі прямокутника,
побудованого на векторах
![]() та
та
![]() .
.
Кутова швидкість та кутове прискорення колеса 3.
Через те що швидкість усіх точок ременя однакова і ковзання ременя по колесах відсутнє, формули зв’язку між колесами 2 та 3 механізму такі:
![]()
Звідси
![]()
При
с,
![]() рад/с2,
рад/с2,
![]() рад/с2.
рад/с2.
Напрямок
швидкості
![]() відповідає напрямку руху точок ременя,
тобто напрямок
співпадає з напрямком
.
Відповідно напрямок
відповідає напрямку руху точок ременя,
тобто напрямок
співпадає з напрямком
.
Відповідно напрямок
![]() співпадає з напрямком
.
співпадає з напрямком
.
Швидкість груза 4.
Через те, що рух від колеса 3 до груза 4 передається нерозтяжною ниткою, то швидкість та дотичне прискорення точки колеса 3, з якої сходить нитка, однакові, тобто
![]() м/с.
При
с
м/с.
При
с
![]() м/с;
м/с;
![]() м/с2, або
м/с2, або
![]() м/с2.
м/с2.
Спрямовані
вектори
![]() та
та
![]() вертикально вниз.
вертикально вниз.
Вказівка. Якщо при визначені швидкості та прискорення одержимо знак “-“, то на нього при визначені їх напрямку можна не звертати уваги, а при кількісних підрахунках брати їх величини із знаком “-“.
Відповідь. В момент часу
 =1сек
швидкість та прискорення точки М:
=1сек
швидкість та прискорення точки М:
 м/с,
м/с,
 м/с2; швидкість та прискорення
груза 4:
м/с2; швидкість та прискорення
груза 4:
![]() м/с;
м/с;
![]() м/с2.
м/с2.
