Поляризация при отражении и преломлении

Пусть естественный свет падает под углом θ₁ на поверхность раздела двух изотропных диэлектриков с показателями преломления n₁ и n₂ (рис.2).

E E E E

θ₁ θ₁

n₁

n₂

θ₂ Е

Е n₂>n₁

Рис. 2.

Обозначим напряженности электрического поля в падающей, отраженной и преломленной волнах соответственно E, E⁽¹, E⁽²⁾. Падающую волну можно представить суперпозицией двух линейно поляризованных волн с взаимно перпендикулярными плоскостями колебаний: в одной из волн плоскость колебаний совпадает с плоскостью падения, в другой – перпендикулярна ей. Напряженностям полей в таких волнах на рис. 2 соответствуют индексы ║ и . Для естественного света E_║ = E . Амплитуды напряженностей электрического поля в отраженной ( E_║⁽¹⁾ и E ⁽¹⁾ ) и преломленной (E_║⁽²⁾ и E ⁽²⁾ ) волнах определяются формулами Френеля. Для характеристики перераспределения интенсивности падающей волны между отраженной и преломленной волнами вводят коэффициенты отражения R и пропускания T , равные отношениям интенсивностей отраженной и преломленной волн, к интенсивности падающей волны. С помощью формул Френеля можно показать, что

,

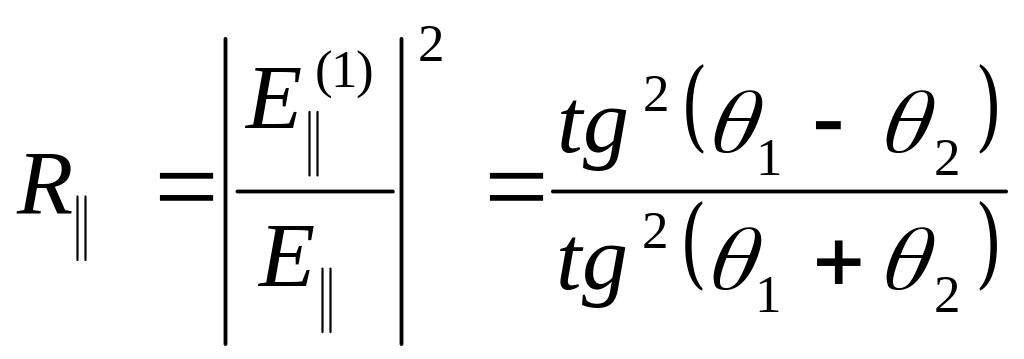, (2)

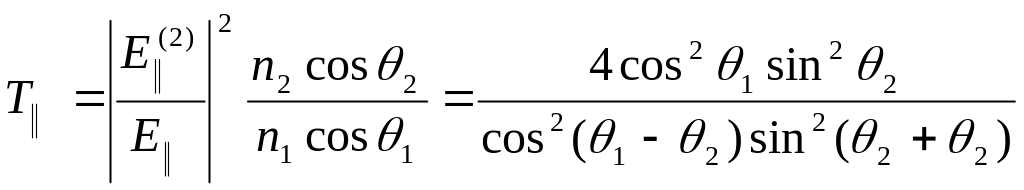
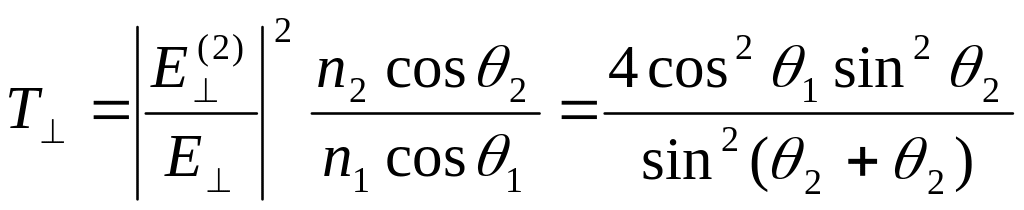
где θ₂ - угол преломления.

На рис. 3 показаны зависимости коэффициентов от угла падения θ₁ световой волны на границу раздела вакуум – стекло.

Из формул (2) видно, что при θ₁+ θ₂=π/2 коэффициенты отражения . Следовательно, в этом случае отраженная волна линейно поляризована в плоскости, перпендикулярной плоскости падения. Проходящая волна поляризована частично; для нее .

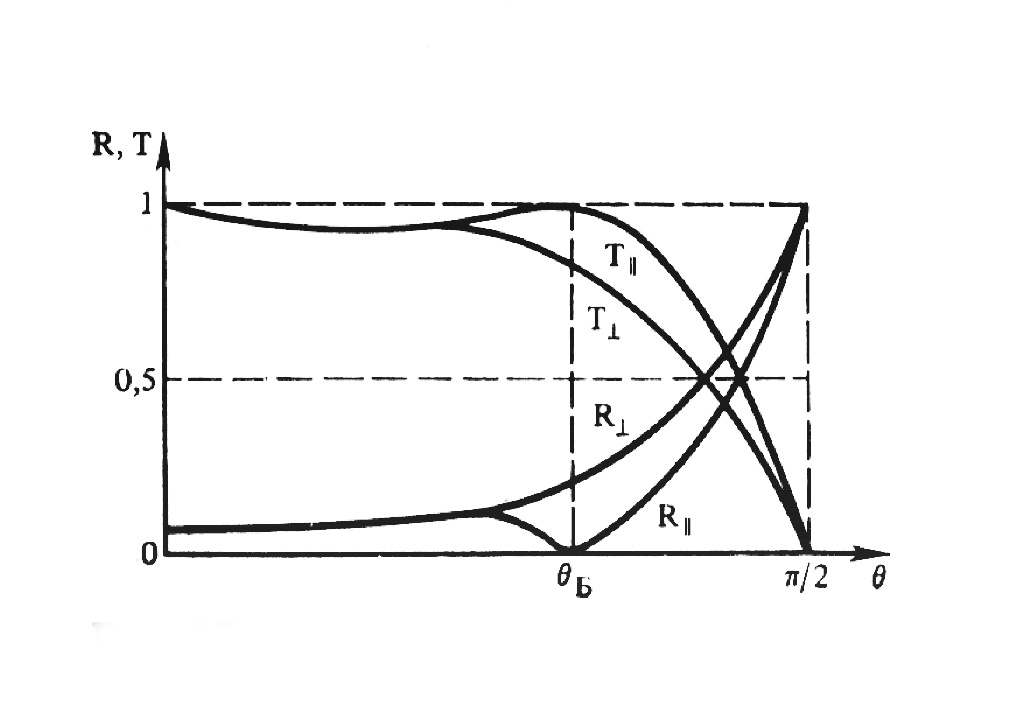
Рис.3

При θ₁+ θ₂=π/2 соотношение (закон Снеллиуса) сводится к виду , при n₁= 1 имеем

. (3)

Последнее равенство определяет угол падения θ₁= θ_Б (рис. 3), при котором коэффициент отражения ; этот угол называют углом Брюстера.

Для преобразования линейно поляризованного света в эллиптически или циркулярно поляризованный применяют оптические элементы, называемые фазовыми пластинками. Фазовые пластинки, изготовленные из анизотропных кристаллов, характеризуются двумя направлениями (осями), лежащими в плоскости входной грани; осью наибольшей (О_б) и осью наименьшей (О_м) скорости распространения света в пластине (рис. 4). Названия этих осей связаны с тем, что линейно поляризованный свет, падающий нормально входной грани пластины, распространяется в ней в зависимости от ориентации плоскости колебаний с разными скоростями v_б и v_м , причем v_б > v_м . Очевидно, фазовая пластинка не изменяет форму поляризации, если свет линейно поляризован вдоль О_б или О_м . Совершенно иная ситуация имеет место, если свет поляризован под некоторым углом α к одной из этих осей, например к оси О_б .

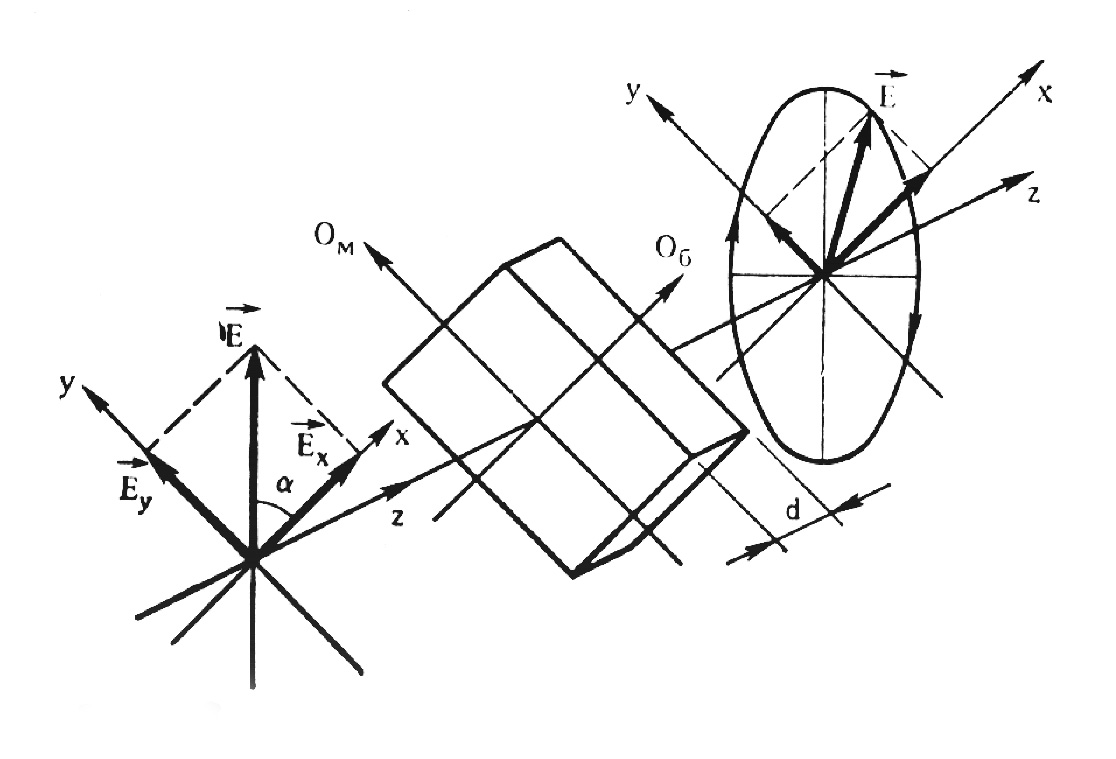
Рис. 4

Направим оси координат x и y вдоль осей O_б и O_м и фазовой пластинки ( ось z по-прежнему совпадает с направлением распространения света ) и рассмотрим напряженность E падающей волны как сумму двух векторов E_x и E_y (рис. 4). Пусть на входе в фазовую пластинку (z = 0) эти векторы изменяются по гармоническому закону с частотой ω и одинаковыми начальными фазами φ_x= φ_y= φ₀ [ см. формулы (1)]. В любой момент времени мгновенные значения векторов E_x и E_y в точках оси z определяются соотношением

,

где v_x и v_y - фазовые скорости световых волн, поляризованных вдоль осей x и y соответственно. На выходе из фазовой пластинки ( z = d ) колебания векторов E_x и E_y определяются выражениями

;

.

При v_x v_y на выходе из пластинки векторы E_x и E_y колеблются с разностью фаз

, (4)

где n_x и n_y - показатели преломления: ; с - скорость света в вакууме.

Из формулы (4) видно, что разность фаз δ зависит от толщины d фазовой пластинки и разности показателей преломления n_x - n_y , которая, в свою очередь, является функцией частоты ω (дисперсия света). В то же время разность фаз δ, как было показано выше, определяет форму кривой, которую описывает конец вектора E = E_x + E_y , то есть форму поляризации световой волны. Таким образом, изменением толщины пластинки и отношения амплитуд векторов E_x и E_y можно получить свет с любой наперед заданной формой поляризации.

Например, для света с длиной волны λ = 0,63 мкм фазовая пластинка из кристаллического кварца имеет n_x = 1,543, n_y = 1,552. При толщине пластинки d = 17,5 мкм разность фаз δ равна π/2 рад. Если, кроме того, амплитуды векторов E_x и E_y равны ( для этого фазовую пластинку поворачивают вокруг оси z таким образом, чтобы азимут поляризации падающего света составлял угол 45⁰ с одной из осей пластинки), то на выходе из пластинки свет циркулярно поляризован.