Свойства определителей

1. Если у определителя какая-либо строка (столбец) состоит из нулей, то определитель равен нулю.

2. Если какие-либо две строки (два столбца) определителя равны или пропорциональны (т.е. элементы одной строки (столбца) получаются умножением элементов другой строки (столбца) на одно и то же число), то определитель равен нулю.

3. Если две строки (два столбца) поменять местами, то определитель изменит знак.

4. Общий множитель элементов любой строки или столбца можно выносить за знак определителя.

5. Если к элементам одной строки (столбца) прибавить соответствующие элементы другой строки (столбца), предварительно умноженные на одно и то же число, то определитель не изменится.

Справедливость этих свойств непосредственно проверяется для определителей второго и третьего порядка. Общее доказательство достаточно громоздко.

Как сказано выше, с помощью этих свойств можно привести определитель к такому виду, у которого есть строка (или столбец), в которой отличен от нуля только один элемент. Для приведения определителя к такому виду необходимо:

1. Вынести общие множители (если таковые имеются) из строк или столбцов за знак определителя (свойство 4.) . Это позволяет уменьшить элементы определителя (что облегчает его дальнейшее вычисление), а также, возможно, получить элементы, равные 1 или (−1), что поможет выполнению следующего пункта.

2. Выбрать строку (или столбец), в которой есть элемент 1 или (−1) (если такие строки или столбцы есть) и с помощью этого элемента (и последнего свойства определителей) обнулять остальные элементы выбранной строки или столбца.

Иллюстрирует сказанное следующий

Пример. = {вынесем 2 из второй строки (свойство 4)} = 2∙ = {С помощью элемента а₂₂=1 и свойства 5 обнуляем все элементы второй строки, кроме самого а₂₂=1. Для этого а) прибавляем к 1-му столбцу 2-ой, умноженный поэлементно на (−5); б) прибавляем к 3-му столбцу 2-ой, умноженный на (−1); в) прибавляем к 4-му столбцу 2-ой, умноженный на (−3)} = 2∙ = {раскладываем определитель по второй строке} = =2∙1∙(−1)²⁺² ∙ = {для облегчения вычисления определителя 3-го порядка выносим (−1) из первых двух столбцов, а из третьего (−2) } = −4∙ 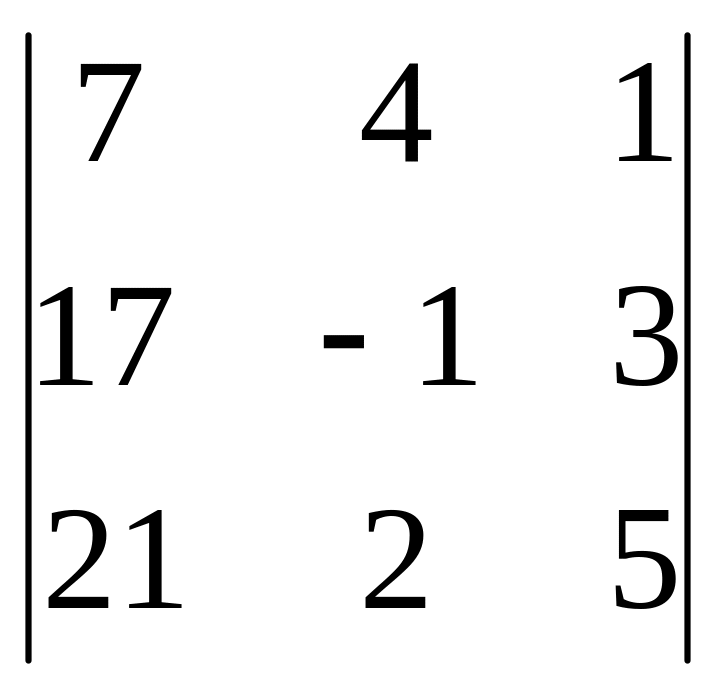= {вычисляем определитель третьего порядка по упрощенной схеме}=−4∙{−35+34+222−(−21+42+340)}=−560.

Обратная матрица

    Рассмотрим обычное простейшее уравнение . Известно, что для его решения необходимо разделить обе части этого уравнения на 2. Деление на 2 можно представить как умножение на число , которое, в свою очередь, может быть записано как : . Число называется числом, обратным к числу 2, поскольку в произведении эти числа дают 1. В общем случае уравнение решается умножением обеих частей уравнения на число (если ), которое называется обратным к числу и определяется как число, дающее в произведении с число 1: . Таким образом, Напомним, что обратное число существует для всех чисел , кроме Сейчас мы по аналогии с обратным числом введем понятие обратной матрицы, которое нам поможет решать уже не одно уравнение, а целые системы уравнений определенного вида.

Матрица называется обратной матрицей для квадратной матрицы , если .    Отметим, что в этом определении обратной матрицы недостаточно требовать, чтобы произведение матриц A и B в каком-либо одном порядке   давало единичную матрицу, так как для матриц нет гарантии, что произведение этих матриц в другом порядке тоже даст единичную матрицу (в общем случае, как мы уже убеждались,    ).

Из определения следует, что обратная матрица B будет квадратной матрицей того же порядка, что и матрица A (иначе, как несложно убедиться, одно из произведений или было бы не определено). Обратная матрица для любой матрицы A единственна (если существует) и обозначается по аналогии с обратными числами. Таким образом, если есть матрица, обратная к матрице A , то выполняется:

.

Для всех ли обратных матриц существуют обратные? Как было сказано раньше, даже не для всех чисел существует обратное: для числа 0 обратного нет. Похожая ситуация наблюдается и с матрицами. Матрица называется вырожденной, если ее определитель = 0. Справедлива следующая

Теорема. Обратная матрица для квадратной матрицы A вида (2) существует тогда и только тогда, когда матрица  A невырожденная. В этом случае обратная матрица единственна и представляется в виде

(5) ,

где − алгебраические дополнения элементов исходной матрицы.

Формула (5) обосновывает следующий алгоритм вычисления обратной матрицы (на примере матрицы размера 3х3) для матрицы

.

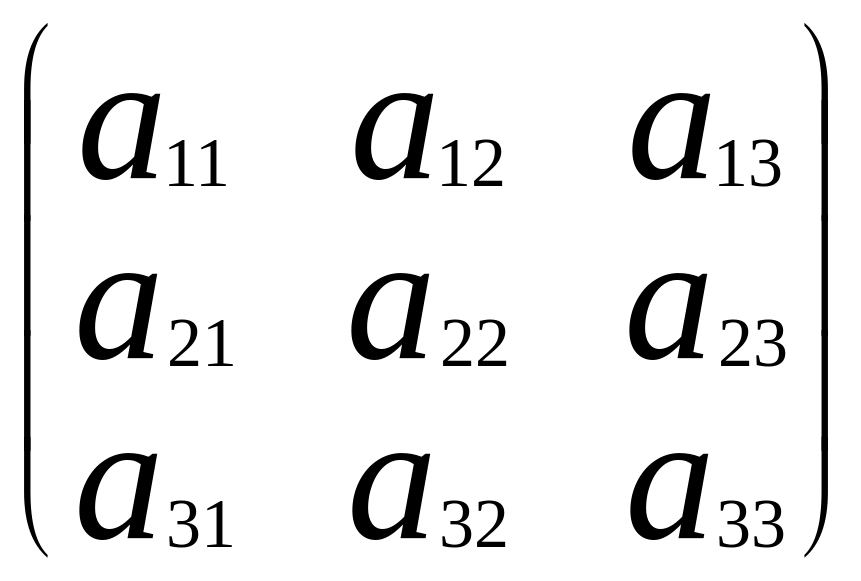1. Вычисляем определитель матрицы      . 

2.   Вычисляем алгебраические дополнения всех ее элементов .

3. Составляем так называемую «союзную» матрицу, заменяя элементы исходной матрицы их алгебраическими дополнениями и транспонируя получившуюся матрицу:

.

4. Составляем обратную:

Пример. Найти обратную для матрицы .

Решение. Воспользуемся тем, что ранее (в параграфе «Определители матриц») для этой матрицы уже были вычислены определитель и алгебраические дополнения всех элементов. Поэтому результаты первых двух пунктов приведенной выше схемы уже есть.

1.      . 

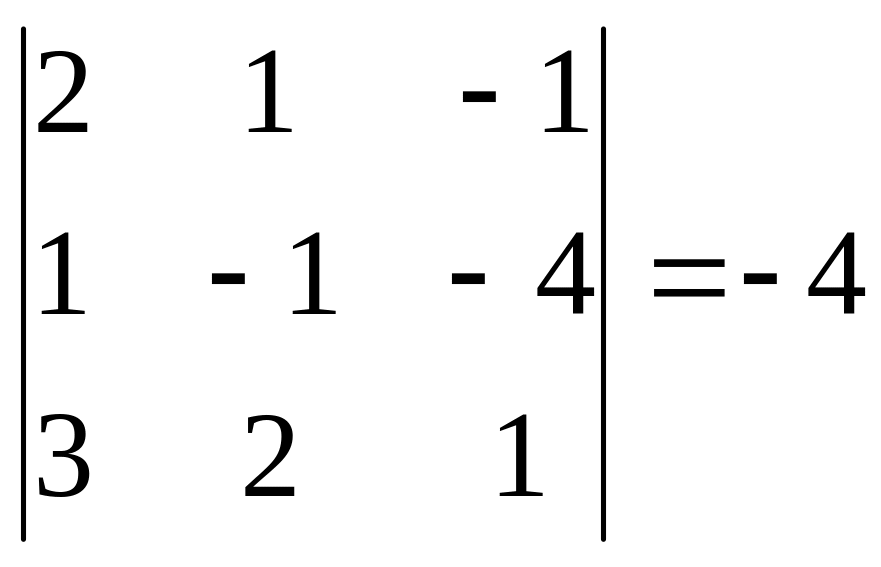2. .

3. «Союзная» матрица :

4. Составляем обратную:

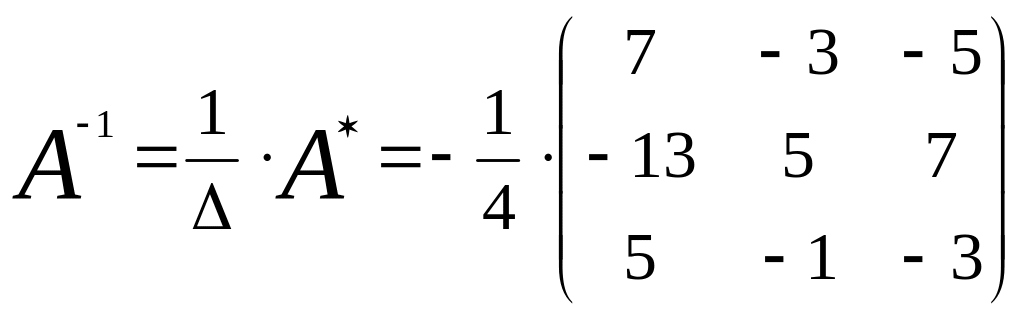
Ответ: .

Можно было произвести умножение числа на матрицу и получить обратную матрицу в обычном матричном виде . При этом матрица уже не выглядит столь компактно, да и дальнейшие действия с ней (например, при решении систем линейных уравнений) производить уже не столь удобно. Поэтому обычно обратную матрицу оставляют в том виде, в котором она дана в Ответе.

Наиболее просто искать по приведенной схеме обратную матрицу для матриц второго порядка. Пусть дана в общем виде матрица второго порядка . Построим обратную матрицу по приведенной выше схеме.

1. D=   . 

2. , , , .

3. .

4. .

Таким образом, обратная для матрицы второго порядка имеет вид:

(5а) , где .

Пример. Найти для матрицы обратную матрицу.

Решение. Определитель . По формуле (5а)

(5б) .