Операции над высказываниями (сложные высказывания)

Используя союзы и словосочетания «и», «или», «не (нет)», «следует (если, …, то….)», «тогда и только тогда, когда» можно из простых высказываний составлять более сложные, истинность которых определяется истинностью составляющих высказываний.

1. Дизъюнкция: А В. Читается: А или В. Высказывание А В истинно, только если истинно хотя бы одно из высказываний А или В.

2. Конъюнкция : А В. Читается: А и В. Высказывание А В истинно, только если истинны оба высказывания А и В.

3. Отрицание: (или ) . Читается: не А. Высказывание истинно, только если высказывание А ложно.

4. Импликация: А В. Читается: из А следует В. Высказывание А В ложно только в случае, когда А истинно, а В ложно.

5. Эквивалентность: А В. Читается: А тогда и только тогда, когда В. Высказывание А В истинно, только если А и В одновременно истинны или одновременно ложны.

Структура теорем (утверждений)

Прямые и обратные (по отношению друг к другу) теоремы иллюстрирует следующий

Пример. Предикаты: – треугольник х – правильный, – углы треугольника х равны. Построим предикаты и .

Прямая теорема: .

В этом случае говорят, что является необходимым условием для , а является достаточным условием для .

Обратная теорема: .

Условие называется необходимым и достаточным для , если истинны одновременно оба высказывания: и .

Законы отрицания сложных высказываний.

Эти законы могут применяться при построении противоположного высказывания при доказательстве «от противного». Доказываются построением таблиц истинности для правой и левой части.

1.

2.

3. (основание метода доказательства «от противного»)

4.

5.

Раздел II. Основы линейной алгебры Матрицы

Матрицей называется прямоугольная таблица чисел . Обозначаются прописными буквами А, В, С, ….. Общий вид матрицы, содержащей m строк и n столбцов:

(1)

Внизу справа при необходимости подписываются размеры матрицы: m – количество строк, n – столбцов. Числа , составляющие матрицу, называются элементами матрицы. Матричные элементы обычно обозначаются той же буквой (только строчной), что и сама матрица, а индексы показывают место элемента матрицы в матрице: первый индекс указывает номер строки, а второй – номер столбца, на пересечении которых находится данный матричный элемент. Например, для матрицы

элементы , …. .

В дальнейшем будет видно, что матрицы (так же как и числа) можно вычитать, складывать, перемножать. Поэтому среди матриц есть аналоги нуля и единицы. Нулевой матрицей называется матрица, все элементы которой равны нулю. Она имеет следующий вид и обозначение: .

Если в матрице (1) поменять местами строчки и столбцы (т.е. первую строчку сделать первым столбцом, вторую строку – вторым столбцом и т.д.), то полученная матрица носит название транспонированной по отношению к исходной матрице и обозначается или :

=

Квадратная матрица – матрица, число строк и столбцов у которой совпадают. Общий вид квадратной матрицы:

(2)

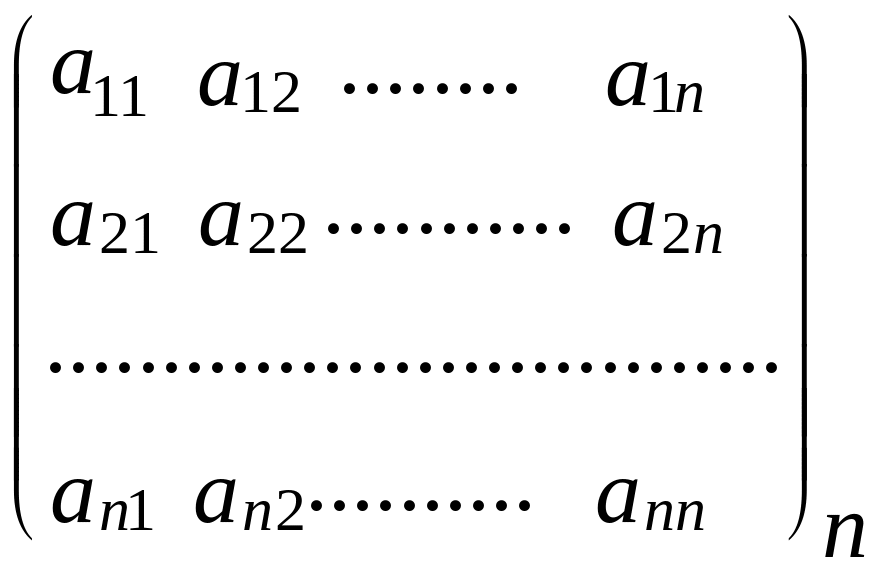
Числа называются главной диагональю квадратной матрицы.

Единичной называется такая квадратная матрица, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю:

(3) Е = .