Кривые второго порядка

Как было сказано выше, общее уравнение прямой имеет вид . Прямые называют также кривыми первого порядка, так как в их общее уравнение координаты и входят в первой степени. Рассмотрим теперь кривые, в уравнение которых, кроме первых степеней координат и , входят и их квадраты, а также произведение координат . Такие кривые называются кривыми второго порядка. Итак, кривые второго порядка − это кривые, уравнение которых имеет вид:

(1) ,

где А, В , С, D, E и F − произвольные числа (первые три – не все равны нулю, конечно, иначе опять получится уравнение прямой). Как бы мы ни меняли числа А, В и С в общем уравнении прямой , все равно будем получать уравнения различных прямых на плоскости. А какого типа кривые могут получаться, если перебирать различные комбинации чисел А, В , С, D, E и F в уравнении кривых второго порядка (1) ? Оказывается, что уравнение (1) в зависимости от коэффициентов может задавать только три типа кривых, а именно, эллипс (окружность – частный случай), гиперболу и параболу. Изучению этих кривых в "удобной" системе координат и займемся.

Окружность

О пределение окружности известно из школьного курса математики.  Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности. Используя формулу расстояния между двумя точками, легко получить уравнение окружности радиуса R, центр которой расположен в точке :

(2) .

Если в уравнении (2) раскрыть скобки (применив формулу квадрата разности), то получим уравнение вида (1), а потому окружность есть кривая второго порядка. Обратно, если в конкретной задаче удалось уравнение кривой второго порядка (1) привести к виду (2), то эта кривая второго порядка есть окружность, а из вида полученного уравнения (2) сразу можно определить координаты ее центра и радиус, что полностью характеризует положение и форму окружности.

Пример 1. Нарисовать окружность с уравнением .

Решение. Уравнение кривой уже имеет вид (2), а потому это уравнение окружности. Далее видно, что данное уравнение получается из общего уравнения окружности при таких значениях параметров: , и . Поэтому это окружность с центром в точке и радиуса 3. Построение такой окружности труда теперь не представляет.

Пример 2. Нарисовать кривую, уравнение которой .

Решение. Попробуем привести это уравнение к виду (2), т.е. к виду суммы квадратов. Для этого отдельно сгруппируем слагаемые с х и с у , добавляя и вычитая подходящие числа : , или . Теперь видно, что это уравнение окружности с центром и радиуса 4. Рисуем.

В этом примере мы сумели преобразованиями привести уравнение вида (1) к виду (2), после чего смогли сделать вывод, что исходная кривая есть окружность, нашли ее центр и радиус. Как сразу понять, будет ли уравнение вида (1) задавать именно окружность? На этот вопрос отвечает

Теорема. Уравнение (1) задает окружность только если , а .

Как видно, исходное уравнение в примере 2 удовлетворяло этим условиям, поэтому нам удалось его свести к виду (2).

Пример 3. Найти уравнение окружности, центр которой лежит на пересечении прямых с уравнениями и и которая проходит через точку .

Решение. Для написания уравнения окружности (2) надо найти координаты ее центра и радиус (точнее, квадрат радиуса ). Координаты центра найдем как координаты точки пересечения прямых с уравнениями и , объединив их в систему и решая ее (см. формулу (5) в параграфе «Прямая линия на плоскости»): . Выражая из первого уравнения и подставляя во второе уравнение, получим , откуда , а потому . Таким образом, координаты центра окружности таковы: , . Осталось найти радиус (или сразу ) . Поскольку известны теперь координаты центра окружности и координаты точки , лежащей на окружности, то радиус можно найти как длину отрезка , используя формулу расстояния между точками с известными координатами (формула (5) параграфа «Свойства координат вектора»). Для тренировки советую так и сделать. Но мы в учебных целях сделаем по-другому. Поскольку мы уже нашли координаты центра окружности , , то частично мы уже можем получить уравнение окружности, подставляя их в (2): . Осталось найти число . Воспользуемся тем, что точка по условию лежит на этой окружности, а потому ее координаты должны удовлетворять уравнению этой окружности. Подставляя в полученное уравнение вместо и числа 2 и 3 (координаты точки А), получим , откуда . Окончательно, уравнение искомой окружности имеет вид .

Для дальнейшего сделаем одно

Замечание по поводу выбора системы координат. Если на плоскости нарисована некоторая окружность радиуса , то для того, чтобы написать ее уравнение, необходимо плоскость сделать координатной, т.е. ввести систему координат (выбрать точку О − начало координат и выбрать направление взаимно перпендикулярных числовых осей х и у) . Сделать это можно бесконечным числом способов. В каждой такой системе координат уравнение данной окружности бу дет иметь вид (2): , где − координаты центра окружности в выбранной системе координат. Но если выбрать систему координат так, чтобы ее начало совпало с центром окружности (см. рисунок), то в такой системе координаты центра окружности будут , , а потому уравнение данной окружности в этой системе координат будет выглядеть наиболее просто: . Такую систему координат, в которой уравнение данной кривой имеет наиболее простой вид, назовем подходящей системой координат для данной кривой. Далее будем искать уравнения кривых, выбирая специальным образом именно подходящую (для этой кривой) систему координат.

Эллипс

Эллипсом называется кривая, состоящая точек плоскости, для каждой из которых сумма расстояний до двух данных фиксированных точек той же плоскости (называемых фокусами эллипса) есть величина постоянная, большая расстояния между фокусами.         

В произвольно выбранной системе координат уравнение эллипса имеет вид уравнения кривой второго порядка (1), в котором могут присутствовать все 6 слагаемых. Но мы выберем подходящую систему координат, в которой уравнение эллипса будет иметь самый простой вид. Каждый эллипс характеризуется положением своих фокусов и тем числом, которому равна постоянная сумма расстояний от точек эллипса до его фокусов. Пусть на плоскости и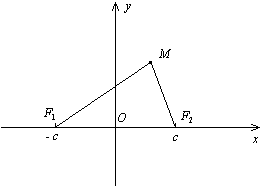 меется некоторый эллипс с фокусами в точках и . Пусть число равно половине расстояния между фокусами. Начало системы координат расположим на середине отрезка . Ось (она будет называться фокальной осью эллипса , так как на ней расположены фокусы эллипса) направим вдоль этого отрезка, ось − перпендикулярно к этому отрезку (см. рисунок). Пусть число − половина суммы расстояний от произвольной точки на эллипсе до фокусов (она одна и та же для всех точек по определению эллипса). Выведем уравнение эллипса в построенной системе координат. По определению уравнения линии на плоскости (см. (1) в параграфе «Уравнение линии на плоскости») нам надо получить соотношение вида , которому удовлетворяли бы координаты любой точки на нашем эллипсе. Пусть − произвольная точка на эллипсе. Какому же соотношению должны в этом случае удовлетворять координаты этой точки и ? По построению системы координат фокусы и в ней имеют координаты (см. рисунок): и . Найдем расстояние от точки до фокусов и по формуле расстояния между точками с известными координатами (это формула (5) из параграфа «Свойства координат вектора» ) : , . По определению эллипса сумма расстояний от точки до фокусов ( т.е. ) должна быть равна 2а (напомню, что а обозначает полусумму расстояний до фокусов). Поэтому координаты любой точки на эллипсе должны удовлетворять соотношению . Это и есть уравнение эллипса, но уж очень неприглядное. Пока даже не видно, что это уравнение кривой второго порядка, так как полученное уравнение совсем не похоже на уравнение вида (1) для кривой второго порядка. Чтобы рассеять сомнения, надо полученное уравнение упростить. Вот схема упрощения. Для избавления от квадратных корней перенесем второй корень в левой части в правую часть (т.е., как говорят, уединим радикал в правой части уравнения) и возведем обе части полученного уравнения в квадрат. После такой процедуры и приведения подобных в уравнении еще останется квадратный корень, но уже один. Снова уединим его и возведем обе части в квадрат. После приведения подобных членов уравнение можно привести к виду: . Для дальнейшего упрощения уравнения введем число по формуле

(3) .

Тогда уравнение запишется в виде . Наконец, разделив обе части уравнения на , получим окончательно:

(4) .

Это и есть простейшее уравнение эллипса в выбранной подходящей системе координат. Оно называется каноническим уравнением эллипса. Числа и называются полуосями (большой и малой) эллипса. Осталось убедиться, что число , которое в ходе преобразований мы ввели по формуле (3), существует. Для этого надо убедиться, что под квадратным корнем в (3) всегда будет стоять положительное число (квадратный корень из отрицательного числа не существует). Это следует из того, что в определении эллипса (еще раз посмотрите на него) указано, что сумма расстояний от точки на эллипсе до фокусов больше расстояния между фокусами. Это значит, что , а потому . Поэтому под корнем в (3) все в порядке.

Перейдем к построению эллипса по заданному его каноническому уравнению (4). Прежде всего, установим, что эллипс представляет собой кривую, симметричную относительно осей координат. Пусть некоторая точка лежит на эллипсе. Это значит, что координаты этой точки и удовлетворяют уравнению эллипса (4), т.е. справедливо равенство

(5) .

Рассмотрим теперь точку , которая является симметричной для точки относительно оси . Тогда ясно, что координатами этой точки будут и , т.е. . Докажем, что точка тоже лежит на том же эллипсе, т.е. ее координаты удовлетворяют уравнению эллипса (4). Подставляя и в (4) вместо и в (4), получаем, что мы должны проверить справедливость следующего равенства: . Поскольку , то это равенство переходит в , что верно с учетом (5) . Итак, вместе с любой точкой на эллипсе на нем же будет и симметричная ей точка относительно оси . Таким образом, эллипс симметричен относительно оси . Точно также легко доказать, что эллипс симметричен и относительно оси . Итак, эллипс симметричен относительно осей координат. Поэтому достаточно построить кусок эллипса, лежащий в 1-ой четверти, затем отразить его относительно оси , а потом то, что получится , отразить относительно оси . Вид же эллипса в первой четверти легко установить (выразив из (4) через : ) методами дифференциального исчисления. Практически же эллипс по заданному его уравнению (4) схематически строят следующим образом. По уравнению определяем числа и (большая и малая полуоси эллипса) − квадраты этих чисел стоят в знаменателях канонического уравнения (4). Затем на оси строим точки, соответствующие числам и , а на оси − числом и . 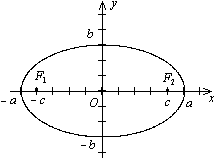Затем соединяют полученные точки так, как это показано на рисунке. Точки пересечения эллипса с осями координат называются вершинами эллипса. Для того чтобы отметить на рисунке фокусы эллипса, надо найти число (это половина расстояния между фокусами), так как координаты фокусов и . Это число легко выразить через числа и из (3):

(6) .

Затем отметить на оси точки и .

Форма эллипса зависит от отношения чисел и в уравнении эллипса (4) (эти числа выше были названы большой и малой полуосью эллипса). Из определения числа в (3) видно, что , а потому . Глядя на приведенный рисунок эллипса, видно, что если отношение близко к 0 (что означает, что число намного меньше числа ), то эллипс сильно вытянут вдоль оси (фокальной оси эллипса). Если же близко к 1 (что означает, что число почти равно ), то форма эллипса близка к круговой. Если , то . В этом случае уравнение эллипса (4) переходит в или , что является уравнением окружности с центром в начале координат. Однако чаще всего в качестве параметра, характеризующего форму эллипса, берут не , а отношение , которое, как увидим дальше, тесно связано с . Величина называется эксцентриситетом эллипса . Как видно − это отношение половины расстояния между фокусами к большой полуоси эллипса. Выразим отношение (которое, как мы убедились, действительно характеризует форму эллипса) через экцентриситет . Из (4) , а потому

(7) .

П оскольку (как ранее отмечали) < , то 0 < 1. Если близко к 0, то из (7) видно, что отношение в этом случае близко к 1, а потому форма эллипса близка к круговой. При получаем , а потому (как отмечалось ранее) эллипс переходит в окружность. Это будет в том случае, когда , а потому оба фокуса совпадут. Если же близко к 1, то отношение близко к 0, а потому, как отмечалось выше, эллипс сильно вытянут вдоль оси (фокальной оси эллипса). Приведенные ситуации отражены на рисунках.

В каноническом уравнении эллипса (4) , как уже отмечалось, . Какую же кривую задает уравнение того же вида

фокусы

,

если в нем ? При таком соотношении параметров это уравнение также определяет эллипс, но его фокусы уже расположены на оси у и имеют координаты и , где (см. рисунок).

Эллипс обладает многими замечательными свойствами. Траектории небесных тел (кометы, планеты) имеют форму эллипса, один из фокусов которого есть Солнце. Траекториям планет соответствует маленький эксцентриситет, поэтому они близки к круговым. Траекториям комет соответствует эксцентриситет, близкий к 1, а потому они сильно вытянуты, а сами кометы то приближаются к Солнцу, то отдаляются от него на большие расстояния. Кроме того, если из одного фокуса выходит в плоскости эллипса луч света, то, отразившись от самого эллипса, он обязательно пройдет через другой фокус. Возьмем поверхность, образованную вращением эллипса вокруг большой оси, и будем считать, что внутри она зеркальная. В один из фокусов поместим источник света. Тогда все лучи, выходящие из источника, отражаясь от поверхности, пройдут через другой фокус, то есть освещенность в обоих фокусах будет одинаковой.

Пример 1. Построить кривую 2-го порядка с уравнением . Решение. Убедимся, что это уравнение эллипса. Для приведения уравнения к виду (4) перенесем число 36 в правую часть, а затем разделим обе части получившегося уравнения на 36, получим . Теперь понятно, что данным уравнением задается эллипс с параметрами , . Строим.

Пример 2. Найти каноническое уравнение эллипса, проходящего через точки и . Решение. Каноническое уравнение любого эллипса имеет вид , но у каждого эллипса свои величины полуосей и , а потому разные числа в знаменателях уравнения. Найдем и для искомого эллипса. Поскольку точки и лежат на эллипсе, то при подстановке их координат в его уравнение вместо и должны получаться верные равенства. Делая такую подстановку, получаем такую систему уравнений:

. Подставляя найденные значения и в уравнение , получаем искомое уравнение эллипса .

Пример 3. Найти каноническое уравнение эллипса в эксцентриситетом , проходящего через точку . Решение. Снова ищем уравнение эллипса в виде . Осталось составить систему из двух уравнений для нахождения числовых значений для и . Первое, как и в предыдущей задаче, получается, если в уравнение эллипса вместо и подставить координаты лежащей на нем точки . Получим . Ясно, что для получения второго уравнения надо использовать известное значение эксцентриситета . По формуле (7) получаем = . Таким образом, получаем систему уравнений: . Из второго уравнения , а потому . Подставляя найденное выражение для в первое уравнение системы, получим . Умножая обе части уравнения на , будем иметь , откуда . Тогда . Подставляя найденные значения и в уравнение эллипса, получаем искомое: . Можно, конечно, упростить (хотя полученное уравнение уже не будет каноническим уравнением): или .