Однородные системы

Исследуем произвольную однородную систему линейных уравнений:

.

В этом случае ранги основной и расширенной матриц совпадают ( ) . Это следует из того, что расширенная матрица получается из основной добавлением нулевого столбца, а потому среди ненулевых миноров расширенной матрицы не может быть таких, которые не входили в основную матрицу. По теореме Кронекера-Капелли (см. параграф «Исследование общих систем линейных уравнений. Теорема Кронекера-Капелли») из этого следует, что любая однородная система совместна. Очевидно, что одним из ее решений всегда является решение , которое называется нулевым (или тривиальным) решением однородной системы. Учитывая теорему Кронекера-Капелли, легко найти условия, при которых однородная система имеет и ненулевые решения.

Утверждение 1. Однородная система линейных уравнений имеет ненулевые решения (причем бесконечное число их) в том и только в том случае, когда ранг ее основной матрицы меньше числа неизвестных: .

Рассмотрим случай, когда число уравнений в однородной системе совпадает с числом неизвестных ( ) :

.

На основании предыдущего Утверждения 1 легко доказать следующее

Утверждение 2. Однородная система из n линейных уравнений с n неизвестными имеет ненулевые решения только в том случае, если определитель основной матрицы этой системы .

Найдем вид общего решения таких систем на примере трех уравнений с тремя неизвестными:

(9) .

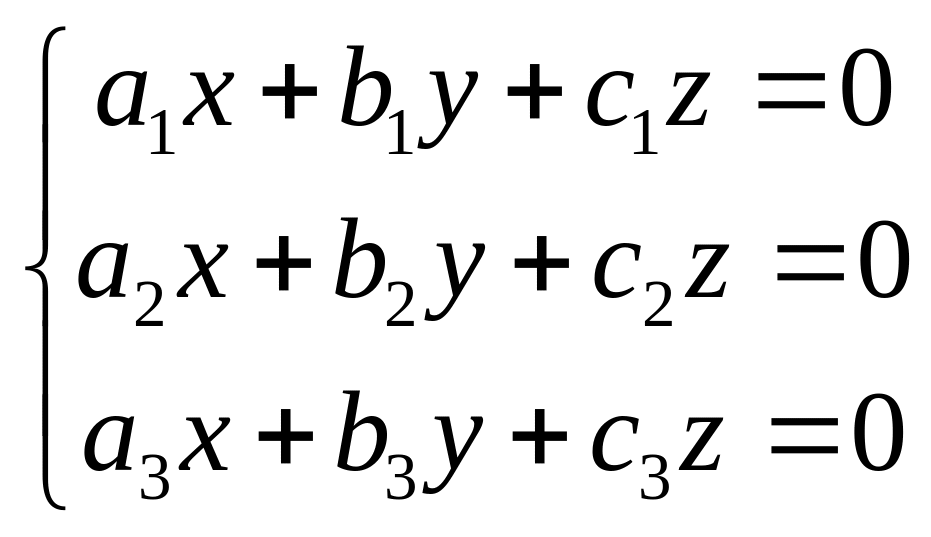Как отмечалось, однородная система всегда совместна, поскольку всегда имеет нулевое решение . Если определитель основной матрицы системы , то это нулевое решение единственно. Пусть . Это означает, ранг основной матрицы системы не может быть равен 3, а потому . Предположим, что ранг основной матрицы . Это означает, что хотя бы один из миноров второго порядка не равен 0. Пусть, например, минор , а потому является базисным минором. В системе (9) оставим только те уравнения, коэффициенты которых участвуют в образовании базисного минора. Таким образом, в системе (9) оставляем только первые два уравнения и приходим к системе

(10) .

Можно показать, что системы (9) и (10) эквивалентны (т.е. имеют одни и те же решения), а потому найдя общее решение системы (10), получим и общее решение исходной системы (9).

Перенесем в (10) слагаемые с переменной в правую часть и рассмотрим полученную систему

как систему двух уравнений с двумя неизвестными x и y при произвольном значении переменной . Поскольку основной определитель этой системы , то по правилу Крамера она имеет единственное решение и при произвольном значении переменной . Применяя формулы Крамера, для этого решения получаются следующие формулы:

(11) , ,

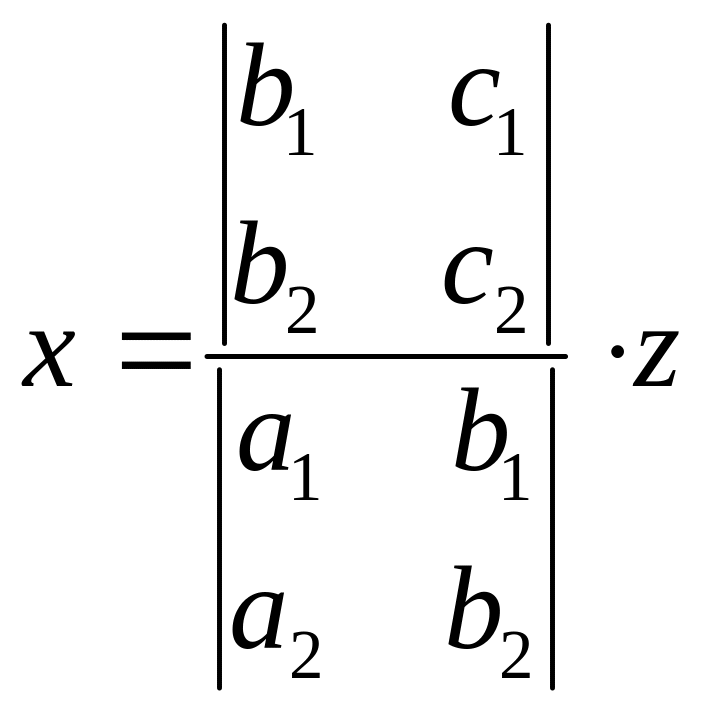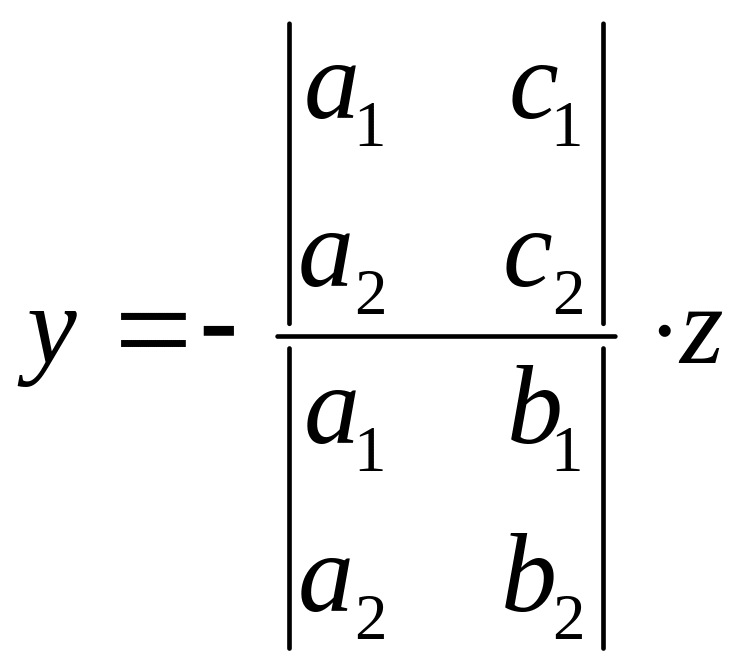где может принимать произвольное числовое значение. Таким образом, формулы (11) представляют общее решение системы (10) . Для того, чтобы запись общего решения выглядела более симметричной, обозначим 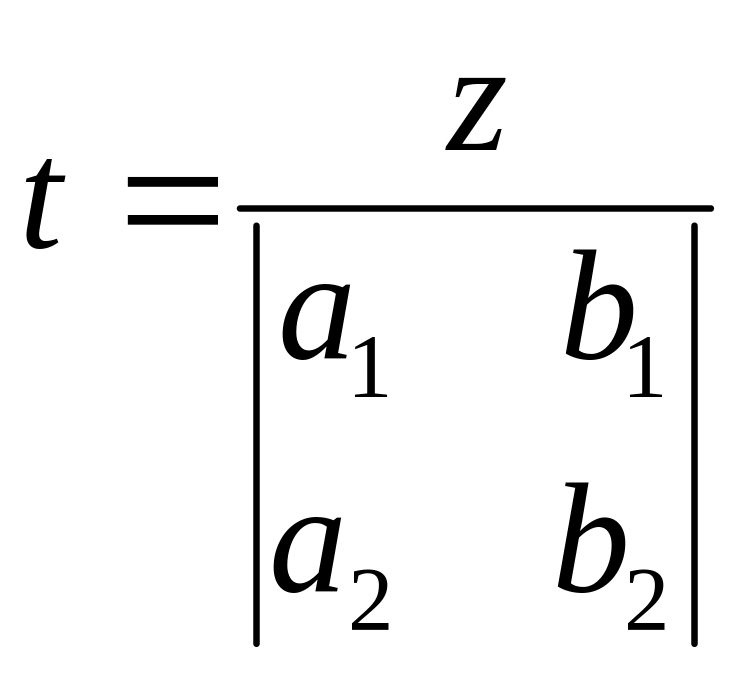. Поскольку z может быть любым числом, то и t тоже может принимать любые числовые значения. Выражая и подставляя в (11), получим общее решение исходной системы (9) в следующем симметричном виде :

(12) , .

При каждом числовом значении параметра t эти формулы дают одно из решений системы (например, при получим нулевое решение системы ). Обратно, любое решение однородной системы получается из приведенных формул (12) при некотором значении параметра t.

Пример. Найти общее решение системы .

Решение. По формулам (12) получаем

, , т.е. , .

Иногда требуется из бесконечного множества решений однородной системы выделить решения, обладающие каким-либо дополнительным свойством.

Пример. Найти решение предыдущей системы , удовлетворяющее условию .

Решение. Как было только что выяснено, общее решение системы имеет вид: , , , . Найдем значение параметра t , при котором решение удовлетворяло бы и дополнительному условию x² − 3y²+z+4=0. Подставляя в него , , , получим или , откуда . Итак, нужное нам решение получается из общего решения при , а потому имеет вид: , , .

Замечание. Фактически мы нашли решение системы уравнений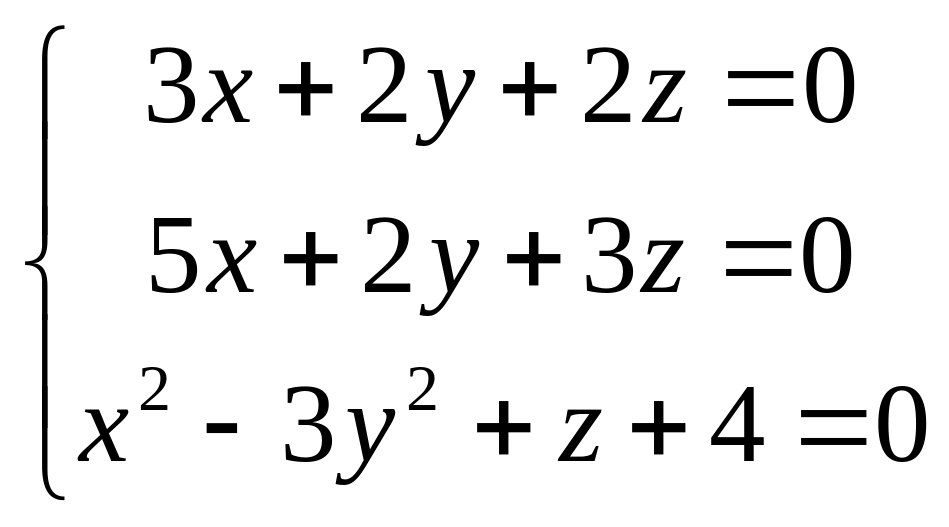 .