Щоб уникнути „мертвого” положення окремих ланок механізму в наступних варіантах треба внести корективи:
рядок 3, схеми 12 та 15 – γ = 60о;
рядок 4, схеми 1 та 11 – β = 120о;
рядок 4, схема 7 – ψ = 150о;
рядок 1, схема 7 – φ = 0о;
в) для розв’язання завдання використати принцип можливих переміщень.
Таблиця 2.7
Рядок R1 |
α |
β |
γ |
φ |
ψ |
k |
М1 |
М2 |
Q |
град |
Н/см |
Нм |
Н |
||||||
0 |
90 |
120 |
120 |
90 |
60 + 3 δ |
160 |
360 |
180 |
320 |
1 |
90 |
120 |
150 – 2 δ |
90 |
30 + δ |
120 |
280 |
260 |
240 |
2 |
0 |
60 |
60 + δ |
0 |
120 |
90 |
220 |
320 |
180 |
3 |
60 |
150 |
120 – 3 δ |
90 |
30 |
100 |
240 |
300 |
200 |
4 |
30 |
60 + 2 δ |
30 |
0 |
120 – 2 δ |
110 |
260 |
280 |
220 |
5 |
30 |
120 |
150 – δ |
0 |
60 |
130 |
300 |
240 |
260 |
6 |
60 |
I50 – 3 δ |
150 – 3 δ |
90 |
30 |
140 |
320 |
220 |
280 |
7 |
0 |
60 + 3 δ |
30 |
0 |
120 – 2 δ |
150 |
340 |
200 |
300 |
8 |
90 – 3 δ |
150 |
120 – δ |
90 – 3 δ |
30 + 3 δ |
180 |
380 |
160 |
340 |
9 |
30 + 3 δ |
30 |
60 – δ |
0 + 3 δ |
150 |
80 |
200 |
340 |
160 |
Рис. 2.10
Рис. 2.11
Рис. 2.12
З а в д а н н я д-7. Визначення реакцій в’язей в складеній балці
Для заданої складеної балки (рис.2.14), яка завантажена у відповідності зі схемою на рис.2.13 та даних з табл.2.8, визначити реакції опор за допомогою принципу можливих переміщень. Перевірити отримані результати методами статики шляхом складання трьох рівнянь рівноваги для всієї конструкції.
Покласти b = 1 м, М = Р b, q = (P + F) / 2b. Номер схеми на рис.2.14 відповідає числу R1, а номер рядка – числу С.
Вказівка: для розв’язання завдання використати принцип можливих переміщень.
Таблиця 2.8
Рядок С |
F |
Р |
φ |
коефіцієнти (для рис.2.13) |
||
кН |
град |
β1 |
β2 |
k |
||
0 |
6 |
4 |
135 |
0 |
3 |
1 |
1 |
5 |
7 |
30 |
1 |
6 |
7 |
2 |
8 |
2 |
225 |
2 |
5 |
3 |
3 |
1 |
5 |
330 |
1 |
2 |
5 |
4 |
7 |
7 |
60 |
0 |
4 |
5 |
5 |
6 |
6 |
120 |
1 |
5 |
3 |
6 |
9 |
3 |
45 |
0 |
2 |
11 |
7 |
9 |
7 |
150 |
2 |
6 |
7 |
8 |
7 |
5 |
210 |
4 |
6 |
5 |
9 |
5 |
3 |
30 |
2 |
4 |
7 |
10 |
7 |
3 |
120 |
0 |
5 |
1 |
11 |
2 |
6 |
240 |
3 |
5 |
3 |
12 |
5 |
5 |
150 |
1 |
4 |
5 |
13 |
9 |
І |
45 |
2 |
4 |
11 |
14 |
2 |
8 |
300 |
0 |
6 |
9 |
15 |
3 |
7 |
30 |
2 |
3 |
11 |
З а в д а н н я Д-8. Дослідження руху механічної системи за допомогою загального рівняння динаміки
Використовуючи загальне рівняння динаміки, перевірити розв’язок завдання № 4. Визначити також натяги двох ниток системи.
Примітка: якщо студент не виконує завдання 5, то можна замість загаль-ного рівняння динаміки використати принцип Даламбера для механічної системи.
Рис. 2.13
Рис.2.14
З а в д а н н я Д-9. Застосування рівнянь Лагранжа другого роду до
вивчення руху механічної системи
На одну з ланок вантажопідйомного механізму (рис. 2.15, 2.16), який знаходився в стані спокою в початковий момент часу, починає діяти обертальний момент М, а на іншу ланку – момент сил опору M0 .
Визначити величину зазначену в табл.2.9 знаком " ? ". Тіла, для яких радіуси інерції не задані, вважати за диски. Якщо необхідно, то покласти m4 = m1 + m2 .
Вказівка: для розв’язання задачі застосувати рівняння Лагранжа 2-го роду.
Вихідні дані взяти з табл. 2.9 (рядок R1), номер схеми відповідає числу С.
Таблиця 2.9
Рядок R1 |
m1 |
m2 |
m3 |
M |
M0 |
r2 = R |
R2 R |
R1 R |
i2Z R |
? |
кг |
Нм |
м |
||||||||
0 |
10 |
30 |
180 |
900 + 20 t |
30 |
0,30 |
1,5 |
1,00 |
1,00 |
ω1(t) або ω4(t) |
1 |
5 |
30 |
175 |
880 + 20 t |
20 |
0,30 |
1,8 |
0,80 |
1,25 |
V3(t) |
2 |
15 |
8 |
180 |
760 + 20 t |
30 |
0,25 |
2,0 |
0,80 |
1,00 |
ε1(t) або ε4(t) |
3 |
15 |
80 |
190 |
980 + 40 t |
40 |
0,30 |
1,5 |
0,90 |
1,00 |
S3(t) |
4 |
25 |
10 |
175 |
880 + 50 t |
40 |
0,30 |
2,0 |
0,60 |
1,50 |
S3(t) |
5 |
6 |
20 |
210 |
980 + 10 t |
40 |
0,20 |
1,6 |
1,25 |
1,00 |
φ1(t) або φ4(t) |
6 |
40 |
25 |
200 |
950 + 10 t |
90 |
0,25 |
1,8 |
0,80 |
1,20 |
φ1(t) або φ4(t) |
7 |
20 |
10 |
150 |
620 + 20 t |
80 |
0,20 |
2,0 |
0,75 |
1,25 |
V3(t) |
8 |
15 |
30 |
200 |
850 + 40 t |
50 |
0,20 |
2,0 |
1,00 |
1,25 |
a3(t) |
9 |
20 |
10 |
175 |
850 + 30 t |
50 |
0,20 |
2,2 |
1,00 |
1,50 |
φ1(t) або φ4(t) |
Рис. 2.15
Рис. 2.16
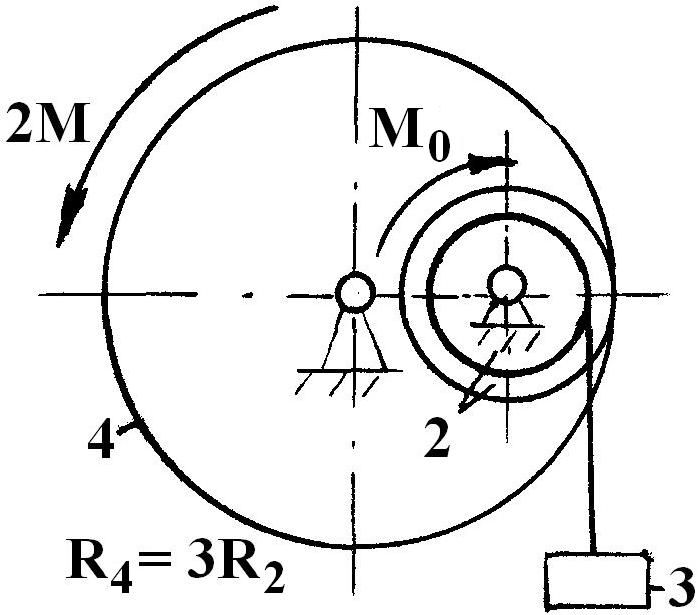
Рис. 2.17