2.2. Основное уравнение молекулярно-кинетической теории газов

Это уравнение устанавливает взаимосвязь между давлением газа (термодинамическим параметром) и средней кинетической энергией теплового движения его молекул (механической характеристикой системы). С точки зрения молекулярно-кинетической теории, давление газа на стенку сосуда является результатом многочисленных ударов молекул газа о стенку. При огромном числе молекул, находящихся в сосуде, одновременно будет производиться огромное количество ударов о стенки. Поэтому достаточно малые и очень быстро меняющиеся силы, порождаемые отдельными ударами, будут складываться практически в постоянную силу, давления, действующую на каждую единицу площади стенок сосуда.

Найдем давление идеального газа на стенку сосуда. Сила, с которой газ действует на стенку, определяется упругими столкновениями молекул со стенкой и, в соответствии со вторым основным законом динамики, равна импульсу, передаваемому стенке всеми молекулами за единицу времени, а давление газа найдется как отношение этой силы к площади стенки. При этом будем считать, что идеальный газ – это система, состоящая из исчезающе малых по размерам твердых шариков конечной массы, хаотически движущихся во всем доступном им объеме, не взаимодействующих на расстоянии и сталкивающихся между собой и со стенками сосуда по законам соударения упругих шаров.

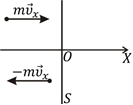
Выделим на поверхности сосуда, в который газ заключен, малую площадку S. Вследствие малости ее можно считать плоской. Введем декартову систему координат, направив ось X перпендикулярно выделенной площадке, как показано на рис. 2.2. С площадкой S могут столкнуться только те молекулы, которые летят в ее направлении, т.е. у которых x-компонента скорости Предположим сначала, что все подлетающие к площадке молекулы имеют одно и то же значение этой x-компоненты. При упругом ударе молекулы о площадку знак этой скорости, а значит, и импульса меняются на противоположный, не изменяя своей величины. 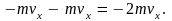Изменение импульса одной молекулы при столкновении с площадкой составит Здесь – масса молекулы. Импульс, переданный площадке этой молекулой, в соответствии с законом сохранения импульса, будет

Рис. 2.2

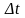За время до площадки долетят и столкнутся с ней только те молекулы, которые в начальный момент находились от площадки на расстоянии, не большем v_xΔt, и занимали объем слоя пространства, примыкающего к площадке. Число ударов молекул о площадку за время будет равно числу молекул, находящихся внутри этого слоя, т.е. 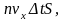где n – концентрация молекул газа. Импульс, переданный площадке этими молекулами, составит

Предположение, что все молекулы газа имеют скорости с одной и той же компонентой v_x, конечно, не верно. Скорости v_x у всех молекул разные и каждая молекула, ударяясь о площадку, вносит свой вклад. Учтем, однако, что нам требуется оценить только коллективный эффект, возникающий от столкновения с площадкой большого числа молекул. Этот эффект описывается средним значением полученного выше выражения. Именно средний импульс определяет силу давления молекул на стенку сосуда. Усредняя это выражение по всем , примем во внимание, что не все молекулы с одним и тем же значением сталкиваются с площадкой, а только те из них, у которых x-компонента v_x > 0. Учтем также, что в равновесном состоянии движение молекул является полностью беспорядочным. Поэтому число молекул, летящих к площадке S и от нее, в среднем одно и то же. Это означает, что среднее значение для v_x > 0 вдвое меньше среднего значения для всех v_x. Таким образом, оказывается, что за время площадка S со стороны газа получит импульс, в среднем равный 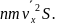Разделив этот импульс на промежуток времени , получим среднее значение силы, с которой газ действует на данную площадку, а разделив затем эту силу на площадь площадки S, найдем давление, оказываемое газом на площадку:

Вследствие беспорядочности движения молекул средние значения квадратов компонент вектора скорости будут одинаковы. А так как 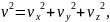то для средних значений всех квадратов компонент скорости будем иметь

(2.5)

С учетом этого находим

(2.6)

Отсюда видно, что давление идеального газа определяется только концентрацией молекул, их массой и средним значением квадрата скорости молекулы.

Правую часть этой формулы можно записать в виде где – среднее значение кинетической энергии поступательного движения молекулы. Учитывая это, получим

(2.7)

Это и есть основное уравнение молекулярно-кинетической теории газов. Основным его называют потому, что это первое соотношение, которое было получено на основе представления о газе как о совокупности быстро и хаотически движущихся частиц. Его называют также уравнением Клаузиуса.