5.1 Критерій -Пірсона [2]

Перевірку за критерієм -Пірсона проводять для об’ємів вибірок , коли параметри математичної моделі визначені за емпіричними даними. Інтервали емпіричного та теоретичного розподілів, в яких теоретична частота , об’єднують с сусідніми інтервалами. При цьому кількість отриманих інтервалів групування може бути менше або дорівнює початковій кількості інтервалів, тобто . Спостережуване значення критерію обчислюється за формулою:

, ( ).

Кількість ступенів вільності дорівнює:

,

де - кількість параметрів математичної моделі.

Стосовно вибору рівня значимості доцільно дотримуватися наступного правила: якщо , то , а при , . Критичне значення знаходять з таблиць критичних точок. Якщо - стосовно передбачуваного закону відкидають.

5.2 Розподіли статистик непараметричних критеріїв згоди при простих гіпотезах [3]

5.2.1 Критерій Колмогорова

У разі простих гіпотез граничні розподіли статистик даних критеріїв згоди Колмогорова, Смірнова, і Мізеса відомі і не залежать від виду спостережуваного закону розподілу і, зокрема, від його параметрів. Говорять, що ці критерії є “вільними від розподілу”. Це достоїнство зумовлює широке використання даних критеріїв на практиці.

Розподіл статистики

, (5.5)

де – емпірична функція розподілу, – теоретична функція розподілу, – об'єм вибірки, було одержано Колмогоровим в [2]. При розподіл статистики сходиться рівномірно до розподілу Колмогорова:

. (5.6)

Найчастіше в критерії Колмогорова (Колмогорова-Смірнова) використовується статистика виду [3]:

, (5.7)

де

, (5.8)

, (5.9)

, (5.10)

- об'єм вибірки, - впорядковані за збільшенням вибіркові значення, - функція закону розподілу, згода з яким перевіряється. Розподіл величини при простій гіпотезі в межі підкоряється закону Колмогорова .

Якщо для обчисленого за вибіркою значення статистики виконується нерівність

,

то немає підстав для відхилення гіпотези .

5.2.2 Критерій Смірнова

У критерії Смірнова використовується статистика

(5.11)

або статистика

, (5.12)

значення яких обчислюються за еквівалентними співвідношеннями (5.9),(5.10).

Реально в критерії звичайно використовується статистика

, (5.13)

яка при простій гіпотезі в межі підкоряється розподілу з числом ступенів свободи, рівним 2.

Гіпотеза не відкидається, якщо для обчисленого за вибіркою значення статистики

.

5.2.3 Критерії

У критеріях типу відстань між гіпотетичним і істинним розподілами розглядається в квадратичній метриці.

Гіпотеза , що перевіряється, має вигляд

(5.14)

при альтернативній гіпотезі

, (5.15)

де - оператор математичного сподівання, - задана на відрізку ненегативна функція, щодо якої передбачається, що , , інтегруються на відрізку . Статистика критерію виражається співвідношенням

, (5.16)

де

, .

При виборі для критерію Мізеса одержують статистику вигляду (статистику Крамера-Мізеса-Смірнова)

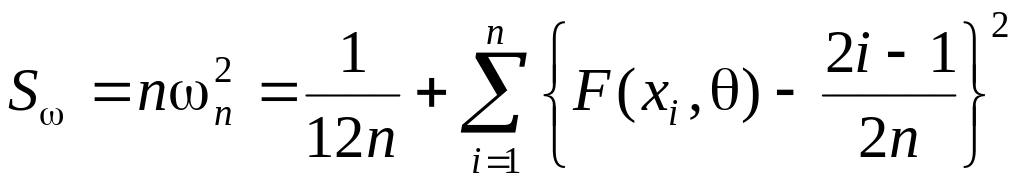, (5.17)

яка при простій гіпотезі підкоряється розподілу, що має вигляд

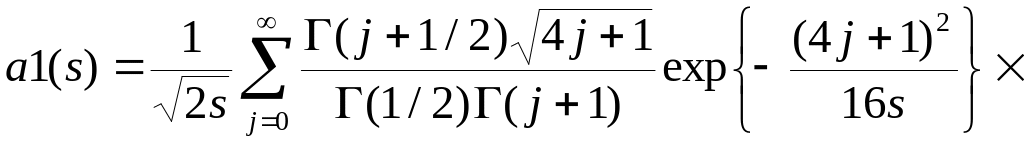
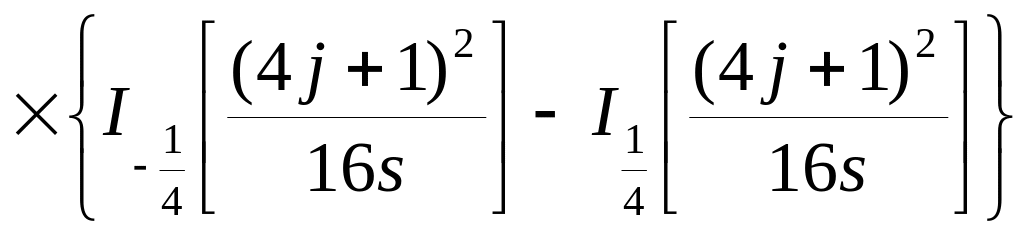, (5.18)

де - модифіковані функції Бесселя,

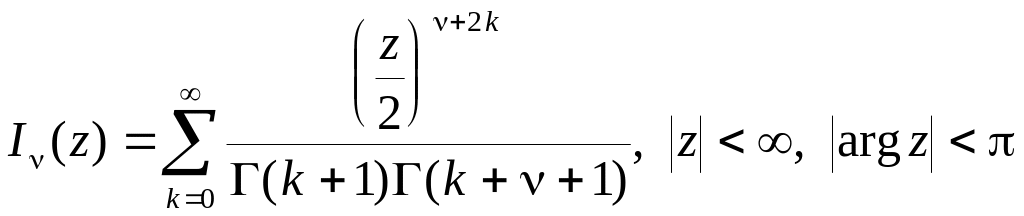. (5.19)

При виборі для критерію Мізеса статистика набуває вигляд (статистика Андерсона-Дарлінга)

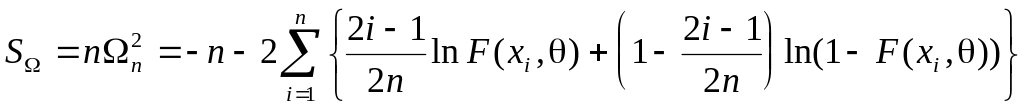. (5.20)

На межі ця статистика підкоряється розподілу, що має вигляд

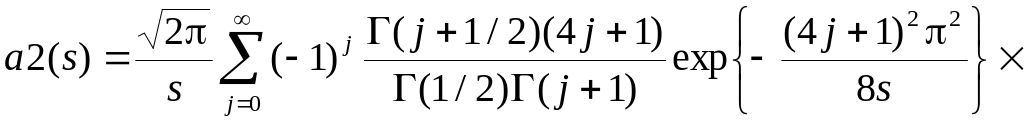
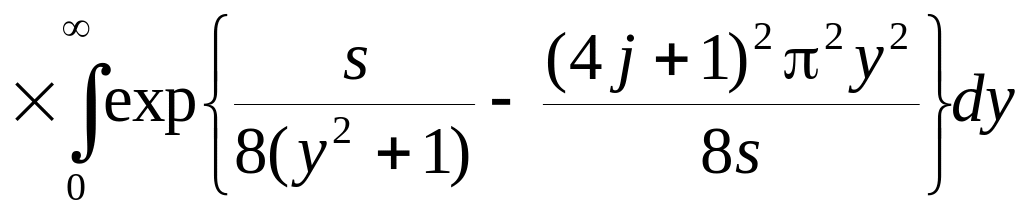. (5.21)

Гіпотези про згоду не відкидаються, якщо виконуються нерівності

і .