Решение.
1 способ. Представим число z
= –1 в тригонометрической форме. Для
этого изобразим его на плоскости (рис.
9). Из рисунка видно, что r
= 1, φ = π. (можно было найти по формулам)
способ. Представим число z
= –1 в тригонометрической форме. Для
этого изобразим его на плоскости (рис.
9). Из рисунка видно, что r
= 1, φ = π. (можно было найти по формулам)
Т огда
огда
 .
.
Корень степени n = 2,
отсюда k = 0, 1.
 Ф =
Ф =
 .
.
Подставим в формулу
.
При k = 0:
 .
.
При k = 1:

 .
.
Изобразим корни на окружности радиуса
 (рис. 10).
(рис. 10).
2 способ. Представим число z
= –1 в показательной форме:
 .
.
При k = 0:
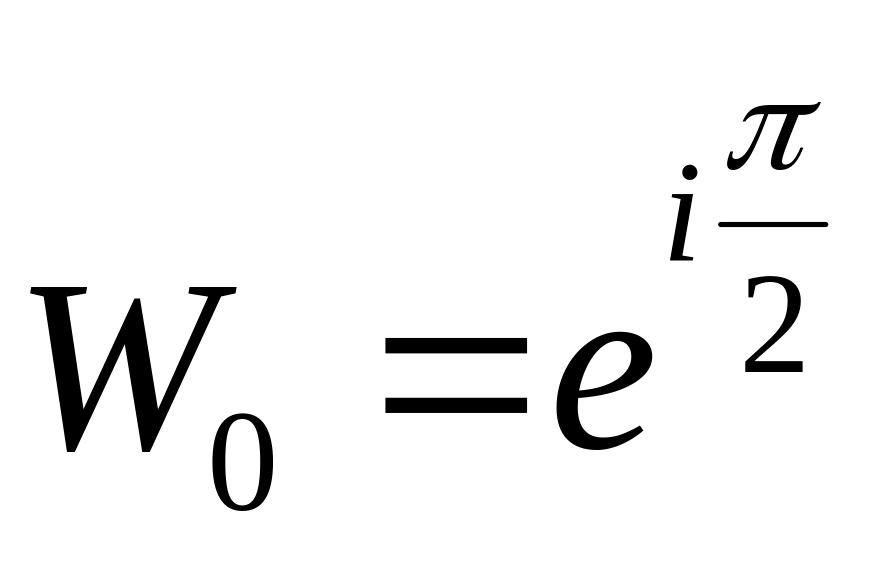 ,
при k = 1:
,
при k = 1:

Свойства комплексных чисел
Переместительный закон сложения: z1
+ z2 = z2
+ z1;
Сочетательный (ассоциативный) закон:
z1 + (z2
+ z3) = (z1
+ z2) + z3;
Переместительный закон умножения: z1
· z2 = z2
· z1;
Распределительный (дистрибутивный)
закон: z1 · (z2
+ z3) = z1
z2 + z1
z3.


 способ. Представим число z
= –1 в тригонометрической форме. Для
этого изобразим его на плоскости (рис.
9). Из рисунка видно, что r
= 1, φ = π. (можно было найти по формулам)
способ. Представим число z
= –1 в тригонометрической форме. Для
этого изобразим его на плоскости (рис.
9). Из рисунка видно, что r
= 1, φ = π. (можно было найти по формулам) огда
огда